International Journal of Innovative Research in Science, Engineering and Technology

International Journal of Innovative Research in Science, Engineering and Technology

Menu

ISSN ONLINE(2319-8753)PRINT(2347-6710)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

LRS Bianchi Type –I Universe with Magnetized Wet Dark Fluid

S. P. Kandalkar1, A. P. Wasnik2, M. N.Gaikwad3
  1. Department of Mathematics, Govt. Vidarbha Institute of Science & Humanities, Amravati, India
  2. Department of Mathematics, Bhartiya Mahavidhyalaya, Amravati, India
  3. Department of Mathematics, Govt. Poly. College, Amravati, India
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology

International Journal of Innovative Research in Science, Engineering and Technology

Abstract

Some locally rotationally symmetric (LRS) Bianchi type I cosmological model of universe filled with dark energy from a wet dark fluid in the presence and absence of magnetic field is in investigated in general theory of relativity . We assume F23 is non vanishing component of Fij. We obtain exact solutions to the field equation, where a relation between metric potential 𝑏 = 𝑎𝑛 is considered. The geometrical and kinematical properties of the models and the behaviours of the anisotropy of the dark energy have been carried out.

Keywords
Bianchi type- I space- time, Magnetic field Wet dark fluid, Dark energy.

INTRODUCTION
The nature of the dark energy component of the universe [1-3] remains one of the deepest mysteries of cosmology. There is certainly no lack of candidates: cosmological constant, quintessence [4-6], k-essence [7-9], phantom energy [10-12]. Modifications of the Friedmann equation such as Cardassian expansion [13,14] as well as what might be derived from brane cosmology [15-17] have also been used to explain the acceleration of the universe. A particular case of the linear Equation of state has used in the cosmological context by Xanthopuolos [18], he considered space-times with two hypersurface orthogonal, space-like, commuting killing fields. The current standard model of cosmology implies the existence of dark energy which accounts for about 70% of the total energetic content of the universe, which ac-cording to the observations is spatially flat [19]. Several models have been proposed to explain dark energy [20-28]. An alternative consists of to consider a phenomenological decaying dark energy density with continuous creation of matter [28] or photons [29,30].The dark energy might decay slowly in the course of the cosmic evolution and thus provide the source term for matter and radiation. Different such models have been discussed and strong constraints come from accurate measurements of the CMB. Although some authors [31] have suggested cosmological model with anisotropic and viscous dark energy in order to explain an anomalous cosmological observation in the cosmic microwave background (CMB) at the largest angles. Bianchi type models have been studied by several authors in an attempt to understand better the observed small amount of anisotropy in the universe. The same models have also been used to examine the role of certain anisotropic sources during the formation of the large-scale structures we see in the universe today. Some Bianchi cosmologies, for example, are natural hosts of large-scale magnetic fields and therefore, their study can shed light on the implications of cosmic magnetism for galaxy formation. The simplest Bianchi family that contains the flat FRW universe as a special case are the type-I space-times. In this work, we use Wet Dark Fluid (WDF) as a model for dark energy. The solution of the field equations for (LRS) Bianchi type I space- time are found. Some physical and kinematical parameter are also evaluated for the solution. A brief summary is given in the last section . We consider string cosmology for Bianchi Type-I metric
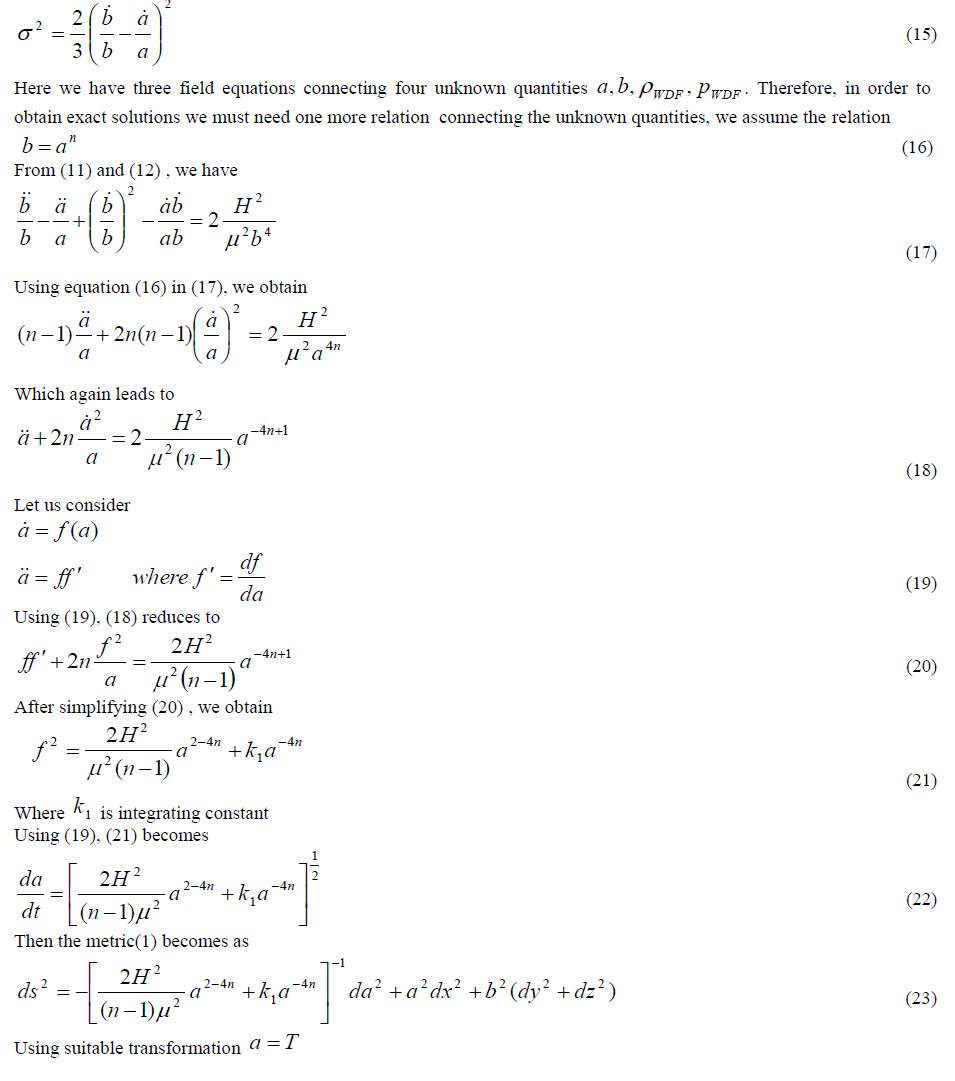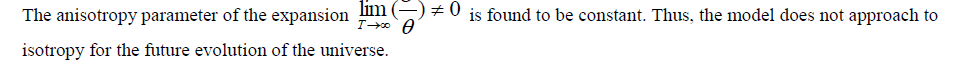image
image
image
image
image

II.CONCLUSION
In summary, we presented LRS Bianchi type-I string cosmological models in the form of Wet Dark Fluid in the presence and absence of magnetic field. We adopt a relation between metric potentials The solution describes a shearing non-rotating model with a big bang start. In the absence of magnetic field, pressure and density of WDF is same.

References
  1. A. G. Riess, et al., ―observational Evidence from supernovae for an accelerating universe and cosmological constant,‖ The Astronomical Journal, Vol. 116, No. 3, 1998, p. 1009.
  2. S. Perlmutter, et al., ―Measurements of Ω and from 42 High-Redshift Supernovae,‖ The Astronomical Journal, Vol. 517, No. 2, 1999, p. 565.
  3. V. Sahni, ―Dark Matter and Dark Energy,‖ Cornell Uni-versity Library, Ithaca, 2004.
  4. B. Ratra and P. J. E. Peebles, ―Cosmological Consequences of a Rolling Homogeneous Scalar Field,‖ Physical Review D, Vol. 37, No. 12, 1988, pp. 3406-3427.
  5. R. R. Caldwell, R. Dave and P. J. Steinhardt, ―Cosmo-logical Imprint of an Energy Component with General equation of state,‖ Physical Review Letters, Vol. 80, No. 8, 1998, pp. 1582-1585.
  6. T. Barreiro, E. J. ― Quinte Sence Arinsing from Exponential Potential‖ Review D, Vol. 61, No. 12, 2000, pp. 127301-127305.
  7. C. Armendariz-Picon, T. Damour and V. Mukhanov, ―K -Inflation,‖ Physical Letters B, Vol. 458pp. 209-218.
  8. C. Armendariz-Picon, V. Mukhanov and P. J. Steinhardt, ―Essentials of K-Essence,‖ Physical Review D, Vol No. 10, 2001, pp. 103510-103523.
  9. P. F. Gonzalez-Diaz, ―K-Essential Phantom Energy :Dooms-day around the Corner?‖ Physical L 1-2, 2004, pp. 1-4.
  10. R. R. Caldwell, ―A Phantom Menace? Cosmological Con-sequences of Dark Energy Component with Super Negative Equation of State,‖ Physical Letters B, Vol. 545, 2002, pp. 23-29.
  11. S. M. Carroll, M. Hoffman and M. Trodden, ―Can the Dark Energy Equation-of-State Parameter be less than–1?‖ Physical Letters D, Vol. 68, No. 2, 2003, pp. 23509- 23520.
  12. E. Elizalde, S. Nojiri and S. D. Odintsov, ―Late-Time Cosmology in a (Phantom) scalar-Tensor theory:Dark Energy and the Cosmic Speed up,‖ Physical Letters D, Vol. 70, No. 4, 2004, pp. 043539-043559.
  13. K. Freese and M. Lewis, ―Cardassian Expansion Model in which the Universe is Flat, Matter Dominated and Accelerating,‖ Physical Letters B,Vol. 540, No. 1-2, 2002, pp. 1-8.
  14. P. Gondolo and K. Freese, ―Fluid Interpretation of Car-dassian Expansion,‖ Physical Letters D, Vol. 68, N,2003, pp. 063509-063519.
  15. C. Deffayet, G. R. Dval ―Accelerated Universe from Gravity Leaking to Extra Dimensions‖ Physical Letters D, Vol. 65, No. 4, 2002, pp. 044023- 044032.
  16. G. Dvali, G. Gabadadze and M. Porrati, ―4D Gravity on a Brane in 5D Minkowski Space,‖ Physical L 485, No. 1-3, 2000, pp. 208-214.
  17. G. Dvali and M. S. Turner, ―Dark Energy as a Modification of the Friedmann Equation,‖ Cornell University Library, Ithaca, 2003
  18. B. C. Xanthopuolos, ―Perfect Fluids Satisfying a less than Extremely Relativistic Equation of State‖ Mathematical Physics, Vol. 28, No. 4, 1987, pp. 905-913.
  19. D. N. Spergel, et al., ―Three-Year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Implications for Cosmology,‖ The Astrophysical Journal Supplement Series, Vol. 170, No. 2, 2007, pp. 377-408.
  20. J.E. Peebles ―Cosmological constant and Dark Energy,‖ Reviews of Modern Physics, Vol. 75, No. 32, 2003, pp. 559-606.
  21. T. Padmanabhan, ―Cosmological Constant—The weight the Vacuum,‖ Physics Reports, Vol. 380, No. 5-6, 2003, pp. 235-320.
  22. E. Tortora and M. Demianski, ―Two Viable Quintessence Models of the Universe: Confrontations of Theoretical Prediction with Observational Data,‖ Astronomy & Astro-physics, Vol. 431, No. 1, 2005, pp. 27-44.
  23. V. F. Cardone, et al., ―Some Astrophysical Implications of Dark Matter and Gas Profiles in a New Galaxy Cluster Model,‖ Astronomy& Astrophysics, Vol. 429, No. 1, 2005, pp. 49-64.
  24. R. R. Caldwell, ―A Phantom Menace? Cosmological Consquences of a Dark Energy Component with Super-Ne- gative Equation of State,‖ Physics Letters B, Vol. 545, No. 1-2, 2002, pp. 23-29. doi:10.1016/S0370-2693(02)02589-3
  25. P. J. E. Peebles and B. Rathra, ―Cosmology with a Time- Variable Cosmological ‗Constant‘,‖ Astrophysical Journal, Part 2 Letters, Vol. 325,No. 2, 1988, pp. L17-L20.
  26. B. Rathra and P. J. E. Peebles, ―Cosmological consequences of a Rolling Homogeneous Scalar Field,‖ Physi-cal Reviews D, Vol. 37, No.12, 1988, pp. 3406-3427.
  27. V. Sahni and A. A. S ― The case for a Positive cosmological Λ-Term,‖ International Journal of Modern Physics D, Vol. 9, No.4, 2000, pp. 373- 443.
  28. Y.-Z. Ma, ―Variable cosmological Constant Model: The Reconstuction Equations and Constraints from Current Observational Data,‖ Nuclear Physics B, Vol. 804, No. 1-2, 2008, pp. 262-285.
  29. J. A. S. Lima, et al., ―Is the Radiation Temperature- Red- shift Relation of the Standard Cosmology in Accordance with the Data?‖ Monthly Notices of the Royal Astrono- mical Society, Vol. 312, No.4,2000.page No.747-752.
  30. J. A. S. Lima and J. S. Alcaniz, ―Angular size in quintess- ence cosmology,‖ Astronomy & Astrophysics, Vol. 348, No. 1, 1999, pp. 1-5.
  31. T. Koivisto and D. F. Mota, ―Accelerating Cosmologies with an Anisotropic Equation of State,‖ Astrophysical Journal , Vol. 679, No. 1, 2008, pp. 1-5.