MATHEMATICAL MODELING AND SIMULATION OF PERMANENT MAGNET SYNCHRONOUS MOTOR

Abstract

Introduction of permanent magnets toreplace the electromagnetic poles with windings requiring aless electric energy supplysource resulted in compact dc machines. Likewise in synchronous machines, the conventional electromagnetic field poles in the rotor are replaced by the PM polesand by doing so the slip rings and brush assembly are dispensed. With the advent power semiconductordevices the replacement of the mechanical commutator with an electronic commutator in the form of an inverter was achieved. These two developments contributed to the development of PMSMs and Brushless dc machines. Due to many applications of PMSM like Sensor less speed control, appropriate position control, Servo motor,etc. Mathematical modelling of Permanent Magnet Synchronous Motor is carried out and simulated using MATLAB.The most important features of PMSM is its high efficiency given with the ratio of input power after deduction of loss to the input power. There is no field current or rotor current in the PMSM

Keywords

Permanent Magnets, Electronic Commutator, Synchronous motor, MATLAB, PermanentMagnet Synchronous Motor, Sensor less Speed control.

INTRODUCTION

The Permanent Magnet Synchronous motor is a rotating electric machine where stator is a classic three-phase InductionMotor and rotor has permanent magnets. In this respect PermanentMagnet synchronous motor is similar to induction motor expect the rotor magnet field in case of PMSM is produced by permanent magnets. The use of permanent magnet to generate a substantial air gap magnetic flux makes it possible to design highly efficient PM motors. The permanent magnet motors classified based on type of back emfinduced.Permanent magnet synchronous motor has sinusoidal back emf and Brushless DC motors have trapezoidal back emf. The features of PMSM motor are:

 Medium construction complexity,multiple fields. High reliability (no brush wear), even at very high achievable speeds.

 High efficiency.

 Low EMI.

 Driven by multi-phase inverter controllers. Sensor less speed control possible.

 Appropriate for position control.

DYNAMIC MODELLING OF PMSM

The dynamic model of the permanent magnet synchronous machine (PMSM) isderived using a two-phase motor in direct and quadrature axes. This approach is done because of the conceptual simplicity obtained withonly one set of two windings on the stator. The rotor has no windings, only magnets.The magnets are modelled as a current source or a flux linkage source,concentratingall its flux linkages along only one axis. The flux linkages of the stator q and dwindings are derived from first principles. The physical modelling of the machine isdeveloped from which the circuit model is derived.Constant inductance for windings is obtained bya transformation to the rotor by replacing the stator windings with a fictitious set ofd-q windings rotating at the electrical speed of the rotor. The equivalence betweenthe three-phase machine and its model using a set of two-phase windings is derivedand this approach is suitable forextending it to model an n phase machine where n is greater than 2, with a two-phasemachine. The transformation from the two-phase to the three-phase variables of voltages, currents, orflux linkages is derived in a generalized way. Derivations for electromagnetic torqueinvolving the currents and flux linkages are obtained. The differential equations describingthe PMSM are nonlinear.

The following assumptions are made to derive the dynamic model:

1. The stator windings are balanced with sinusoidally distributed magnetomotiveforce (mmf).

2. Theinductance versus rotor position is sinusoidal.

3. The saturation and parameter changes are neglected.

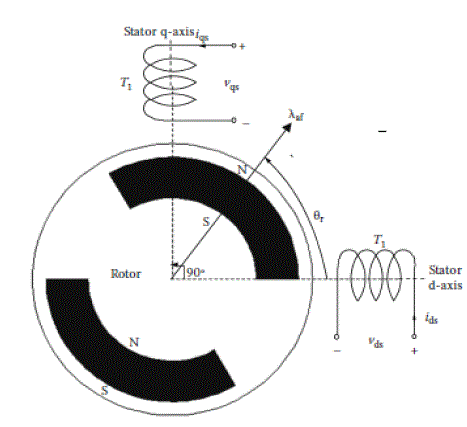
The windings are displaced in space by 90 electrical degrees and the rotor windingis at an angle θr from the stator daxis winding. It is assumed that the q-axis leadsthe d-axis to a counter clockwise direction of rotation of the rotor. A pair of poles isassumed for this figure, but it is applicable with slight modification for any number of pairs of poles. Note that θr is the electrical rotor position at any instant obtained bymultiplying the mechanical rotor position by pairs of electrical poles.The d- and q-axes stator voltages are derived as the sum of the resistive voltagedrops and the derivative of the flux linkages in the respective windings as

In the salient pole PMSMs, the inductances are rotor position dependent.If the rotor position dependency is eliminated by transformation.The relationship between the flux linkages and currentsis uniquely determined by the matrix containing the rotor position terms. From thisrelationship, given the injected currents, the rotor position can be evaluated if the fluxlinkages are known. This aspect of operating with injected signals andon the corresponding flux linkages equations to extract rotor position from inductancemeasurements makes the motor drive system independent of rotor position sensorsthat are expensive, less reliable.

TRANSFORMATIONTOROTOR REFERENCEFRAMES

Reference frames givesa unique view of the system and dramatic simplification of the systemequations. the independent rotor field positiondetermines the induced emf and affects the dynamic system equations of both thewound rotor and the PMSMs. Therefore, looking at the entire system from the rotor,i.e., rotating reference frames, the system inductance matrix (equ.8) becomes independent ofthe rotor position, thus leading to the simplification and compactness of the systemequations. The relationship between the stationary reference framesdenoted by d- and q-axes and the rotor reference frames denoted by dr- and qr-axes. Transformation to obtain constant inductances is achieved by replacing theactual stator and its windings with a fictitious stator having windings on the qr anddr –axes. The fictitious stator will have the samenumber of turns for each phase as the actual stator phase windings and should producethe equivalent mmf. The actual stator mmf in any axis (say q or d) is the product the number of turns and current in the respective axis winding. It is equated,respectively, to the mmf produced by the fictitious stator windings on the q- andd-axes. Similarly, the same procedure is repeated for the d-axis of the actual stator winding. This leads to a cancellation ofthe number of turns on both sides of the q- and d-axes stator mmf equations, resultingin a relationship between the actual and fictitious stator currents. The relationshipbetween the currents in the stationary reference framesand the rotor reference frames currents is written as.

iqds = �� ir and similarly voltage relation is given as qds

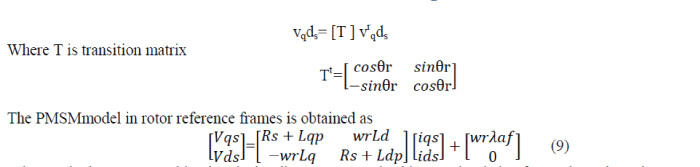Wherewr is the rotor speed in electrical radians per second. This equation is ina form where the voltage vector is equal to the product of the impedance matrixand the current vector, with an additional component due to the motional emf of the rotor flux linkages.

ELECTROMAGNETIC TORQUE

The electromagnetic torque is the most important output variable that determines themechanical dynamics of the machine such as the rotor position and speed. It is derived fromthe machine matrix equation (above) by looking at the input power and its various componentssuch as resistive losses, mechanical power, and the rate of change of storedmagnetic energy. Hence, the outputpower is the difference between the input power and the resistive losses in a steady state.The dynamic equations of the PMSM can be written as

IMPLEMENTING MODELED EUATIONSBYSIMULINK

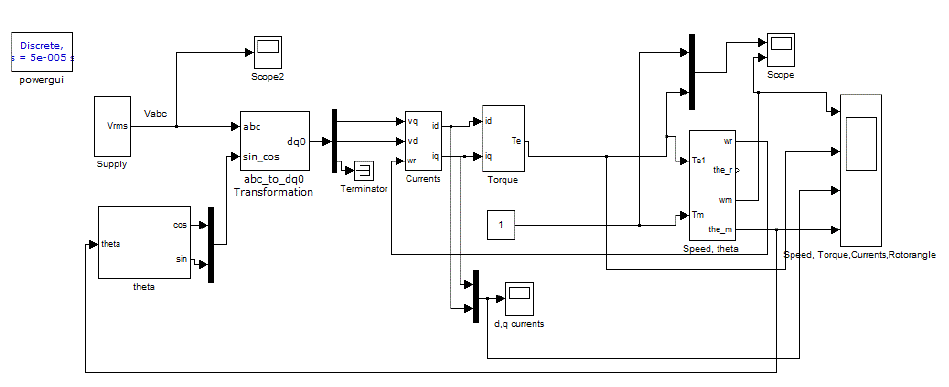
Three pahse supply of Vrms=220V, f=50 Hz is provided as supply. Using Parks Transformation three phase is transformed into two pahse for ease of modelling. Parks Transformation give Direct axis(d), Quadrature axis(d) and zero-sequence currents. Zero sequence currents are terminated.

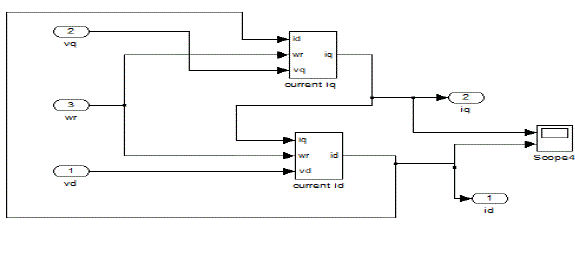
A. Current Subsystem:

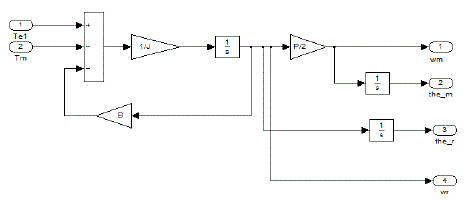
The stator currents iq, id are derived by state space model and these are represented in the subsystems as shown in the fig 2.

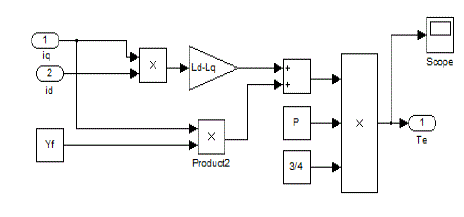
B. Torque Sub model :The electromagnetic equation that is derived equ(14) is implemented in the subsystem as shown in fig 3.

SIMULATION RSULTS

The motor simulation is carried out for with values Stator Resistance Rs= 1.2 B = 4.6752e-5 kg/m^2, J = 2.0095e-5 Nm s, Stator Resistance = 2.0357, Direct axis Inductance(Ld) = 7.8e-3 H, Quadrature axis Inductance(Lq) = 7.8e-3 H , flux – 0.154 V s, Poles=4, Vrms= 220v

CONCLUSION

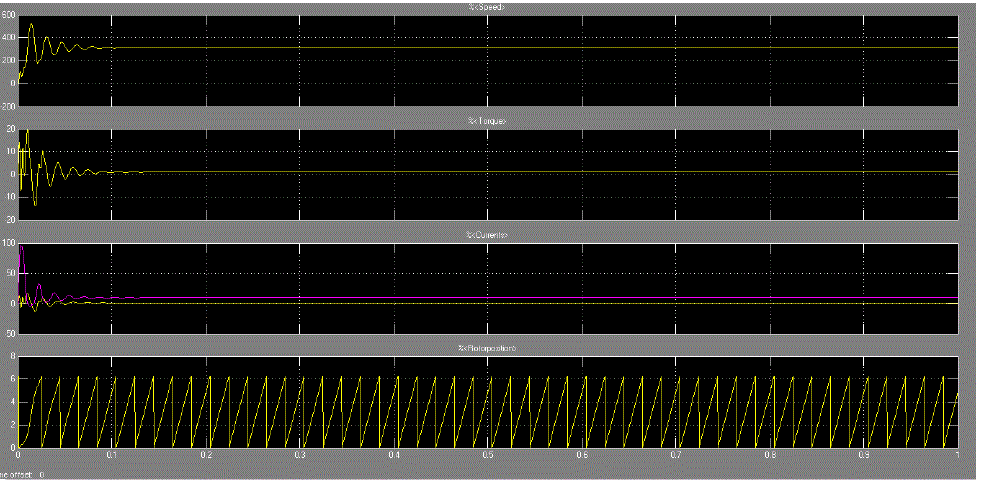
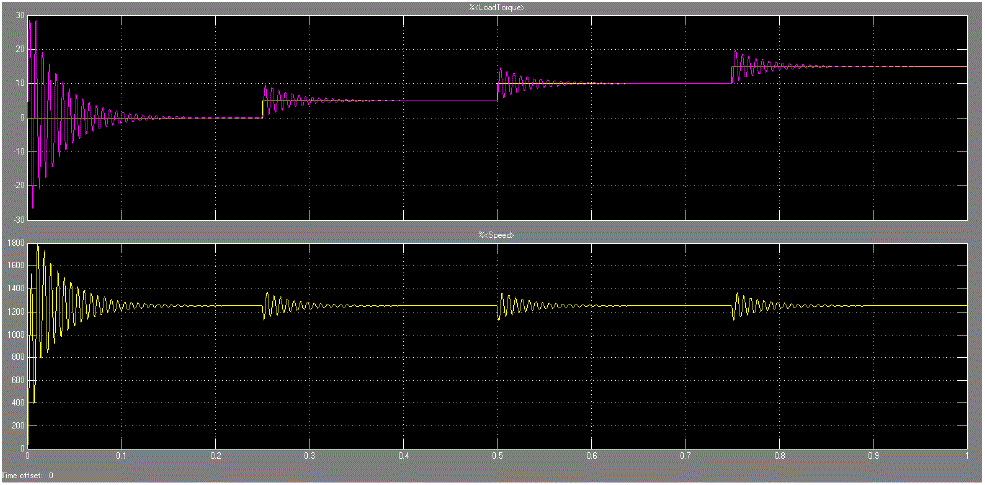
In this paper simulation based mathematical model of permanent magnet synchronous motor is implemented using MATLAB. The simulation results shows the performance characteristics of permanent magnet synchronous motor,i.e. speed of motor remain constant even with variation of load torque. The stator currents and electromagnetic torque magnitudes are also obtained in the graphs. The rotor position found out at every instant and is shown in the graph.

ACKNOWLEDGEMENT

We would like to extend our gratitude and sincere thanks to my supervisor K. NarasimhaRaju for his constant motivation and support during the course of our paper. We truly appreciate and value his esteemed guidance and encouragement from the beginning to the end of this paper.

Figures at a glance

Figure 1 Figure 2 Figure 3 Figure 4 Figure 5 Figure 6 Figure 7

References

R. Krishnan, “Electric Motor Drives Modelling, Analysis and Control”, Prentice Hall, 2001. John Wiley & Sons, Parker, R.J., “Advances in Permanent Magnetism”, 1990. K Parvathy, R. Devanathan.“Linearisation of Permanent Magnet Synchronous Motor Using MATLAB and Simulink”. 10/2011; ISBN: 978-953-307-914-1. R. Krishnan, “Permanent Magnet Synchronous and Brushless DC Motor Drives”, CRC Press,2010.