ISSN: 2319-9873
ISSN: 2319-9873
University of Uyo, Department of Mechanical Engineering, PMB 1017, Uyo, Akwaibom State- Nigeria.
Received: 22 August 2013 Accepted: 13 November 2013
Visit for more related articles at Research & Reviews: Journal of Engineering and Technology
Mathematical modeling of the hardness of case hardened mild steel with respect to carburizing time has been carried out. The work utilized data that was empirically generated at the heat treatment shop of the National Metallurgical Development Centre, Jos. The study established the existence of a relationship between carburizing time and hardness value in Hv of carburized steel as well as the effective case depth in mm. A strong positive correlation coefficient of + 0.98 was found for hardness value and +0.91 was found for effective case depth, both of these relationships were linear. Based on that fact two mathematical models were developed for the prediction of hardness value and effective case depth using simple linear regression method. The result of the work agreed with existing theories on the relationship between carburizing time and hardness of carburized steel
Hardness, Model, Effective case depth, Carburizing time, and Steel.
A model is any representation of reality and may be in graphical, physical or mathematical terms [1]. Mathematical model is commonly used because it tries to show the workings of the real world by means of mathematical symbols, equations, and formulae.
Although mathematical or symbolic models are the more usual, other types of models e.g iconic, analogue, simulation and heuristic sometimes have applicability [1-3]. Model may be further classified into normative and descriptive. Normative models are concerned with finding the best, optimum or ideal solution to a problem. Many mathematical models fall into this classification. Descriptive models, as their name implies, describe the behavior of a system without attempting to find the best solution to any problem. For example simulation tends to fall within this category. Perhaps the most important point to appreciate is not so much what a model is called, but what it does in helping an engineer to attain the goals that they have set [1-3].
Case hardening of mild steel is a common practice in engineering and it is geared towards improving the mechanical properties of mild steel. A case hardened steel component gives rise to a hard case and a soft core a property desirable in shafts, gears, cams, and other machine moving parts. These case hardened materials resist wear, distortion, and increases service life of the component. Case hardening is a very important process in metal properties improvement. There are variables that control the case thickness and hardness of a material during case hardening and this include; temperature, carburizing material, carburizing time, energizers, and subsequent heat treatment. Several efforts have been made to model some engineering processes using mathematical models. Ihom et al [4] modeled the surface hardness of steel using rice husk waste. The authors were able to develop an equation which at any given temperature T in oC , The hardness H of the surface hardened steel can be predicted. The equation they developed is stated below
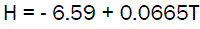 (1)
(1)
Ihom, et al [5] used multiple regression model to study foundry clay- bonded sand mixtures. They developed a mathematical model that can be used to determine the green compression strength of clay bonded sand as influenced by water and clay. Ihom, et al [6] developed a mathematical model for studying the effect of ramming on the mould parameters of Yola natural sand. The invaluable nature of the mathematical models in engineering have equally being demonstrated by several authors here listed [1-3,7].
The objective of this present work is to undertake the mathematical modeling of the hardness of a case hardened mild steel with respect to carburizing time by first establishing that there is a correlation between hardness and carburizing time, then using regression method to develop a model for the relationship.
The data used in this paper has been generated at the heat treatment shop of the National Metallurgical Development Centre, Jos- Nigeria. The data was generated through the classical method of single factor experiments involving a large number of trials. Table 1 shows the chemical composition of the steel used for the pack carburization. Table 2 shows highest hardness value attained in Hv (Vickers hardness) at each carburizing time. Table 3 shows the effective case depth at each carburizing time. The pack carburization was carried out using charcoal as the carburizing material. The highest hardness values were obtained at 0.2mm from the surface of the steel specimens. The carburizing temperature was 900OC. The only variable factor was carburizing time which was varied from 2hrs- 8hrs., and the hardness was the dependent variable.
The basic modeling equations used are as follows;
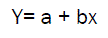 (2)
(2)
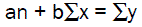 (3)
(3)
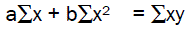 (4)
(4)
Where, n is number of pairs of figures a and b are constants representing the intercept and the slope. b is also called the regression coefficient. X and Y are the variables representing the independent and dependent variables.
Product moment coefficient of correlation (r)
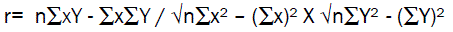 (5)
(5)
This formula is used to find r from the data in Table 2
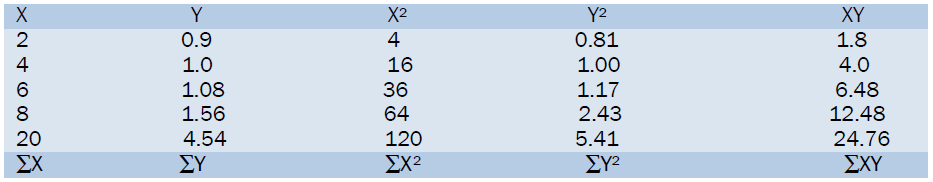
Let
X = t = carburizing time in hrs.
Y = D = Effective case depth in mm
r= 4 x 24.76 – 20 x 4.54/ √4 x 120 – (20)2 x √4 x 5.41 – (4.54)2 = 99.04 – 90.8/ 8.94 x 1.01 = 8.24/ 9.066 = +0.91.
Thus the correlation coefficient is + 0.91 which indicates a strong positive linear association between carburizing time and effective case depth of the pack carburized steel. Based on the existence of a linear relationship, linear regression can be used in developing mathematical model for the relationship between carburizing time and effective case depth.
Equation 5 is also used to find r from the data in Table 3
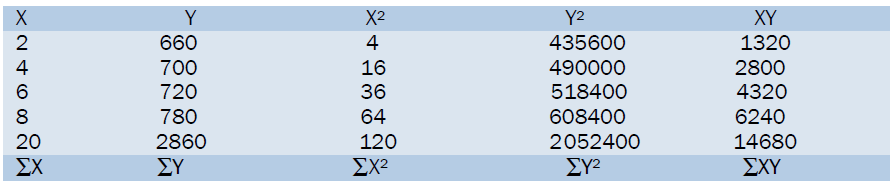
Let
X= t = carburizing time in hrs.
Y = H = hardness values in Hv
r= 4x 14680- 20 x 2860/ √4 x 120- (20)2 x √4 x 2052400- (2860)2 = 58720 – 57200/ 8.94 x 173.21 = 1520/1548.5 = +0.98.
Thus the correlation coefficient is + 0.98 which indicates a strong positive linear association between carburizing time and hardness value. Based on this result linear regression method can be used to model the relationship between carburizing time and hardness value.
The essence of developing a mathematical model is to be able to predict the hardness value or effective case depth that would be obtained at a given carburizing time during pack carburization. This information will ease the work of the process engineer who is handling the case hardening operation [1-6].
Let
X = t = Carburizing time, Y= D= Effective case depth
Using equations 3-4 we come up with these equations
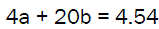 (6)
(6)
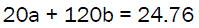 (7)
(7)
Solving the two equations simultaneously we have
b = 0.10
Substituting the value of b into equation 7 we have
a = 0.62
Substituting the values of a and b into equation 2 we have the mathematical model for the relationship between carburizing time and effective case depth in mm.
Let
Y= D= Effective case depth
X= t = carburizing time in hrs.
Y =a +bx (2)
D = 0.62 + 0.10t (8)
With equation 8 if the pack carburization is done for 10 hours using charcoal at 900oC, the effective case depth will be
D= 0.62 + 0.10 X 10 = 1.62mm
Using equations 2-4 we can develop the model
Let xX=t = Carburizing time in hrs, Y = H= Hardness value in Hv
4a + 20b = 2860 (9)
20a + 120b = 14680 (10)
Solving the two normal equations simultaneously we have
b = 19
Substituting b into equation 10 we found the value of a
a = 620
Substituting the values of a and b into equation 2 gives us our regression line and our mathematical model for the relationship between carburizing time and hardness value.
Let Y =H= Hardness values in Hv, X =t = Carburizing time in hrs.
Y =a + bx (2)
H = 620 + 19X (11)
With equation 11 if the pack carburization is done for 10 hours at 900oC using charcoal the hardness value in Hv will be
H= 620 + 19 X 10 = 810Hv
Aramide, et al [8] in their work showed that the hardness of a carburized steel depend on the temperature and also the carburizing time. They also showed that the case depth also depend on the carburizing time and temperature of carburization. Several other authors in their work have shown that these two variables carburizing time and carburizing temperature have a relationship or influence case depth and hardness of the carburized steel [9-12].
The longer the carburizing time the thicker the effective case depth will be and also the harder the steel will be. As the carburizing time increases so also the effective case depth and the hardness of the carburized steel [8-10]. These theories agree with the product moment coefficient of correlation (r) which is a measure of relationship between two variables. The degree of correlation between carburizing time and hardness value is very strong with a correlation coefficient of +0.98 completely agreeing with the above theory that as the carburizing time increases the hardness also increases linearly.
The relationship between carburizing time and effective case depth is also linear and strong but the relationship between carburizing time and hardness value is stronger, since the correlation coefficient of the relationship between carburizing time and effective case depth is +0.91. They are all positive relationships which mean that as the carburizing time is increased both hardness and effective case depth will increase [1,8,9].
With the developed mathematical models the effective case depth and hardness value of carburized steel can be predicted. The result obtained with the mathematical models for 10hrs of carburizing time compared very well with the empirically generated data in Tables 1 and 2.
The examples of the prediction made of the hardness and the effective case depth using 10hrs of carburizing time gave result that is within the range of results in Tables 1 and 2. The use of these models will bring about saving in energy consumption, time and minimize cost [1,12]. The outcome of the operation will also be more certain to the satisfaction of the customers. The equations are valid provided charcoal is used as the carburizing material, the carburizing temperature is kept constant at 900oC and the hardness measurement is taken at 0.2 mm from the surface of the carburized steel.
The mathematical modeling of the hardness of case hardened mild steel with respect to carburizing time has been done. The work has clearly shown that there is a strong positive correlation coefficient (r), between carburising time and effective case depth and also hardness value. This relationship is linear, and based on that premise mathematical models have been developed that can be used to predict hardness values of carburized steel and their effective case depths.