Keywords
|
| Automatic Speech Recognition, Artificial Neural Networks, Pattern Recognition, Back-propagation Algorithm |
INTRODUCTION
|
| Speech recognition is fundamentally a pattern recognition problem. Speech recognition involves extracting features from the input signal and classifying them to classes using pattern matching model. Performance of ASR system is measured on the basis of recognition accuracy, complexity and robustness. The deviation of operating conditions from those assumed during training phase may result in degradation of performance [1]. |
| The primary objective of this research is to explore how a back-propagation neural network can be applied to isolated word speech recognition. The main benefit of this work would be its contribution towards employing the neural network-based techniques for solving common but difficult problem of pattern recognition, particularly in ASR. There are three major types of pattern recognition techniques namely dynamic time warping (DTW), Hidden Markov model (HMM) and artificial neural networks (ANN) [1], [5]. |
| This paper is organized as follows. Section II describes the automatic speech recognition, with a special emphasis on feature extraction. Section III describes artificial neural networks and some algorithms using neurons as their primary elements. Section IV discusses the structure and characteristics of back propagation neural networks. Section V discusses pattern recognition using back propagation neural networks. Finally, section VI concludes the paper. |
AUTOMATIC SPEECH RECOGNITION
|
| Acoustic pattern recognition determines a reference model which best matches the input speech, as an output. Acoustic modelling, naturally posed as a static pattern matching problem is amenable to neural networks. Many ASR systems in existence employ DTW or HMM for feature recognition. DTW method measures the distance between each reference frame and each input frame using the dynamic algorithm to obtain the best warping of the pattern. HMMs characterize speech signals using a pre-trained Markov chain. But, some difficulties still exist in such ASR systems, since speech recognition is a complex phenomenon due to the asymmetries involved in speech production and speech interpretation. For effective results, ASR can employ an approach that is closer to human perception. Neural networks are modelled after the human brain. Hence, we use neural network for feature recognition in our ASR system [1], [2]. |
| In our ASR implementation, the speech waveform, sampled at 8 kHz is used as an input to the feature extraction module. Software ‘Audacity’ is used to record the input speech database. Speech files are recorded in ‘wave’ format, with the following specifications: Fs = Sample rate in Hertz = 8000 and number of bits per sample = 16. We use the Mel-frequency Cepstral Coefficients (MFCC) for feature extraction. The efficiency of this phase is important for the next phase since it affects the behaviour of modelling process. |
| Figure 1 shows the block diagram of an automatic speech recognition system using MFCC for feature extraction and neural network for feature recognition. |
ARTIFICIAL NEURAL NETWORKS
|
| Many tasks involving intelligence or pattern recognition are extremely difficult to automate, but appear to be performed very easily by human beings. Human beings recognize various objects, apparently with very little effort. The neural network of human beings contains a large number of interconnected neurons. Artificial neural networks are the computing systems whose theme is borrowed from the analogy of biological neural networks [2], [4]. |
| Neural network is a useful tool for various applications which require extensive classification. The advantage of parallel processing in neural networks and their ability to classify the data based on features provides a promising platform for pattern recognition. Traditional sequential processing techniques have limitations for implementing pattern recognition problems in terms of flexibility and cost whereas neural networks perform the processing task by training instead of programming in a manner analogous to the way human brain learns. Unlike the traditional sequential machines where rules and formula need to be specified explicitly, a neural network learns its functionality by learning from the samples presented [3], [7]. |
(A) Characteristics of artificial neural networks
|
| Artificial neural networks have a labelled directed graph structure where nodes perform some computations. They consist of a set of nodes and a set of connections connecting pair of nodes. Each connection carries a signal from one node to another. Label represents the connection strength or weight indicating the extent to which signal is amplified or diminished by a connection. Different choices for the weights result in different functions being evaluated by the network. Weights of the network are initially random and a learning algorithm is used to obtain the values of the weights to achieve the desired task. A graph structure, with connection weights modifiable using a learning algorithm,results in a network called artificial neural network. Neural network stores the knowledge specific to a problem in the weights of connections using learning algorithm [3], [7]. |
(B) Classification
|
| Classification means assignment of each object to a specific class or group. It is of fundamental importance in a number of areas ranging from image and speech recognition to the social sciences. We use a training set consisting of sample patterns representing all classes, along with class membership information for each pattern. Using the training set, rules for membership in each class are deduced to create a classifier, which later assigns other patterns to their respective classes according to these rules. We use neural networks to classify samples, i.e., map input patterns to different classes. Each output node can stand for one class. An input pattern is determined to belong to class i if the ith output node computes a higher value than all other output nodes when that input pattern is fed into the network [3], [4]. |
(C) Perceptrons and Linear separability
|
| Perceptron is a machine that learns using examples i.e. training samples to assign input vectors to different classes. Perceptron uses a linear function of inputs. Perceptron has a single output whose value determines to which class each input pattern belongs and it is represented by a single node that applies a step function to the net weighted sum of its inputs. If there exists a line, whose equation is w0+w1x1+w2x2 = 0, that separates all samples of one class from the other class, then a perceptron, with weights w0, w1, w2 for the connections from inputs 1, x1, x2, respectively, can be derived from the equation of that line. Such classification problems are said to be linearly separable, since they are separable by a linear combination of inputs. The inter-relationship between perceptron weights and the coefficients of terms in the equations of lines holds true for the converse as well [3], [7]. |
(D) Limitations of using perceptrons
|
| If there are three input dimensions, a two class problem can be solved using a perceptron only if there is a plane that separates samples to different classes. For simple examples and two dimensional spaces it is relatively easy to determine by geometric construction whether two classes are linearly separable. But it becomes very difficult for higher dimensional spaces. If no line can separate samples belonging to two different classes i.e., the samples are not linearly separable, then a simple perceptron cannot classify the samples. It is the fundamental limitation of simple perceptron. Real life classification problems are linearly non-separable and hence perceptron training algorithm cannot achieve accurate results for such classification problems [3]. |
| A robust algorithm would achieve a reasonable separation between most of the samples of the two classes. Two algorithms achieve robust classification for linearly non-separable classes - pocket algorithm and least mean square algorithm. The LMS algorithm minimizes the mean square error instead of the number of misclassified samples, while the pocket algorithm stores information about the better weight vectors observed in the process of modifying weights [3], [7]. |
(E) Pocket algorithm
|
| This algorithm identifies the weight vector with a longest unchanged run as the best solution among the weight vectors examined so far. The best solution explored so far and the length of unchanged run associated with the best solution is stored in pocket. The contents of the pocket are replaced whenever a new weight vector with a longer successful run is obtained [3], [7]. |
(F) Adalines
|
| Robust recognition may also be achieved by minimizing the mean square error (MSE) instead of the number of misclassifies samples. An adaptive linear element or adaline accomplishes classification by modifying weights in such a way as to minimize the MSE at every iteration training. This can be achieved using gradient descent, since MSE is a quadratic function whose derivative exists everywhere. When the sample input is presented during training the network, the linear weighted net input is computed and compared with the desired output for that sample, generating an error signal. This error signal is used to modify each weight in the adaline. Unlike the perceptron training algorithm, weight changes are made to reduce MSE even when a sample is correctly classified by the network [3], [7]. |
(G) Supervised learning using multi-layer networks
|
| Perceptron approach can be extended to solve linearly non-separable classification problems, using layered structure of nodes. Such networks contain one or more layers of hidden nodes that isolate useful features of the input data. However it is not easy to train these networks. Given that the network makes an error on some sample inputs, identifying which weights in the network must be modified, and to what extent is a tough task. Hence, perceptron and other one layer networks are seriously limited in their capabilities. Feed-forward multilayer networks with non-linear node functions can overcome these limitations, and can be used for many applications. Hence a more powerful supervised learning mechanism called back-propagation is used for multi-class, multi-level discrimination [3], [5]. |
BACK-PROPAGATION NETWORKS
|
| The term back propagation network is used to describe feed-forward neural networks trained using the back propagation learning method. The back propagation algorithm is the modification of least mean square algorithm. It modifies network weights to minimize the mean squared error between the actual and desired outputs of the network. Back propagation algorithm makes use of supervised learning in which the network is trained using training samples for which inputs as well as desired outputs are known. The weights are frozen once the network is trained and it can be used to compute output values for new input samples. The feed forward process involves presenting an input pattern to input layer nodes that pass the input values onto the first hidden layer. Each of the hidden layer nodes computes a weighted sum of its inputs and passes the sum through its activation function before presenting the result to the output layer. An error at a higher layer of multi-layer network is propagated backwards to nodes at lower layers of the network. The gradient of the backward-propagated error measures is then used to determine the desired weight modifications for connections leading into the hidden nodes. In short, weights are modified in a direction corresponding to the negative gradient of an error measure. [3], [7]. |
(A) Architecture of back propagation networks
|
| The back propagation algorithm assumes feed-forward neural network architecture. In this architecture nodes are partitioned into layers numbered 0 to L. Here the layer number indicates the distance of a node from the input nodes. The input layer numbered as layer 0 is the lowermost layer, and the output layer numbered as layer L is the topmost layer. We choose L as 2 i.e., we use a three-layer network. Nodes in the hidden layers neither directly receive inputs from nor send outputs to the external environment. An extra dummy node x0 with constant input equal to 1; is also used so that the threshold or bias term can be treated just like any other weight in the network. The number of nodes in the hidden layer depends on the problem complexity. Each output node and hidden node applies a sigmoid function to its net input. S-shaped sigmoid function is used because it is a monotonically increasing, continuous, invertible, and differentiable function [3], [7]. |
(B) Objectives of back propagation networks
|
| We train the back-propagation network with supervised learning algorithm using a large number of input patterns, say P = 50. For each input vector xp, we have the corresponding desired output vector dp, of dimensions, say K. This collection of input output pairs constitute the training set {xp, dp}. The length of the input vector xp is equal to the number of features of the input pattern. The length of output vector dp is equal to the number of outputs of given application i.e. the number of classes, as decided by the given classification problem [3], [7]. |
| The objective of training the network is to modify the weights so that the network’s output vector is as close as possible to the desired output vector, when a samples input vector is presented to the network. To achieve this objective, the cumulative error of the network needs to be minimized. The difference between the actual output and the desired output represented by error function Err should be non-negative [3], [7]. |
| Equation (1) represents the cumulative error of the neural network. |
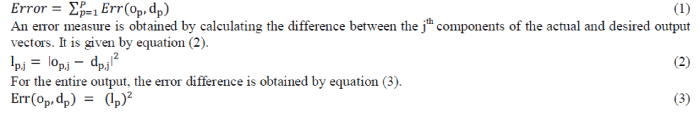 |
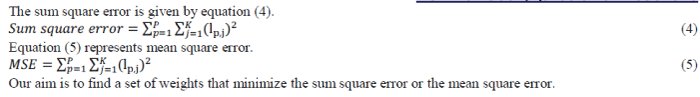 |
PATTERN RECOGNITION USING BACK-PROPAGATION NEURAL NETWORK ON MATLAB
|
| We implemented back-propagation network on MATLAB. The inputs to our implementation are - the input training samples and desired outputs for the training samples, the learning rate, momentum for weight update, satisfactory mean square error, number of layers and the number of nodes in each layer as its inputs. This implementation results in a neural network architecture with final weights of all the links connecting the nodes; computed by minimizing the mean square error, for a given number of iterations of input training samples [3], [7]. |
(A) Inputs to the system
|
| A vector of integers denoted by L represents the number of the layers and number of nodes in each layer of our implementation. There are three types of layers – input layer, hidden layers and output layer. Our implementation has 13 nodes in the input layer, as we are using MFCC algorithm for feature extraction which gives a feature vector of length 13. Also we are designing the ASR system for isolated word speech recognition of ten digits (0-9). So the output layer has 10 nodes. For every presentation of input sample of testing phase, only one output node will have a value of 1, with all the remaining nodes’ outputs as 0. We choose the number of nodes in the hidden layer as 11. |
| Our implementation has two matrices – X and D, as its input. Matrix X represents the training samples. It is a P-by-N matrix, where P equals the number of input training samples and N equals the length of feature vector for each training sample i.e., 13. Matrix D represents the desired output values for the corresponding input training vectors. It is a P-by- K matrix, where P equals the number of input training samples and K equals the number of classes to which the samples are to be classified i.e., 10. We use 50 input samples i.e., 5 input samples per digit, for training the backpropagation network. Hence, P is 50 in our implementation. |
| The learning rate Îî decides the weight-changes occurring in each iteration of the training. We choose learning rate as 0.5. The momentum term in the weight update equation represents how much effect the current error value has on the weight-changes. We choose momentum as 0.2. The satisfactory mean square error value is the mean square error at which the computation terminates. |
(B) Outputs of the system
|
| We store weight vectors (w0, w1, w2…) in weight matrices. There is a weight matrix between each pair of adjacent layers. Initial weights are random. We randomize the weight matrices in the range [-0.5, 0.5]. Each layer, except the output layer has a bias node x0 whose activation is always one. There is a link from each node in layer i to the bias node in layer j (j > i). Weights of all links to the node x0 are assigned as 0. |
(C) Pre-allocation of matrices
|
| For faster computation, we pre-allocate ‘1’ to all the activation vectors (x1, x2, x3, x4….), net vectors (net = w1x1+w2x2+….) and ‘0’ to all the delta weight vectors (Δw). For delta vectors i.e. weight change vectors, two additional matrices representing the delta weights at previous iteration and the sum of delta weights for each presentation of sample input are needed. Both the matrices are P-by-K matrices i.e 50-by10 matrices. |
(D) Feed-forward phase
|
| The outputs i.e. the activation values for all the nodes in each layer are calculated, by applying sigmoid function to the ‘net’ value obtained at each node. The actual output vectors obtained should match with the desired output vectors. Difference between the desired output and the obtained output is error. Error for all samples is calculated and then we compute the running total of the squared error, by adding the errors for all input samples. |
(E) Back-propagation phase
|
| In this phase, backward error propagation of weight adjustment takes place for each sample input pattern. The ith node in the input layer holds a value for xp,i for the pth input pattern. The net input to the jth node in the hidden layer is obtained as follows. |
 |
(F) Termination criteria
|
| Training is continued until a satisfactory low error is achieved, or until the maximum number of iterations is exceeded. We are using per-epoch learning. An epoch consists of a presentation of the entire set of training samples i.e., 50 in our case. We choose 1000 epochs. Weight changes suggested by all the training samples are accumulated together into a single change to occur when the termination criteria is met. Thus weights are updated only after all samples are presented to the network [3]. |
(G) Training the network
|
| Spoken digits were recorded as five samples per digit. Thus, total 50 different recordings were recorded. Then we calculated MFCC coefficients for all the input ‘wave’ files. We choose supervised learning and create target vectors i.e. desired output vectors for inputs. Thus, there are 50 target vectors. The network is trained using both feed-forward phase and back-propagation phase until the termination criteria is met [6]. |
(H) Results
|
| We use 2 samples per digit i.e., 20 samples for testing the network. We test the network after the weights are modified by the training phase. We round off the output vectors for each testing sample to 0 or 1. The recognition rate of our training phase reaches 80 %. |
| The results are summarized in the following table. |
 |
| Thus, accuracy of 80 % was achieved for the testing set of 20 words. A learning rate of 0.5 and momentum of 0.2 were found to give best recognition rate and fast training. |
Figures at a glance
|
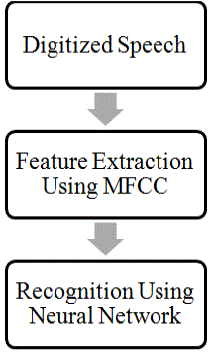 |
| Figure 1 |
|
References
|
- Yuan Meng, Speech recognition on DSP: Algorithm optimization and performance analysis, The Chinese university of Hong Kong, July 2004,pp. 1-18.
- ChauGiang Le, Application of a Back-Propagation Neural Network to Isolated Word Speech Recognition, June 1993.
- KishanMehrotra, Chilukuri K. Mohan, Sanjay Ranka, Elements of Artificial Neural Networks, Penram International, 2007.
- Jayant Kumar Basu, DDebnath Bhattacharya, Tai-hoon Kim, Use of artificial neural network in pattern recognition, International Journal ofSoftware Engineering and Its Applications, Vol. 4, No. 2, April 2010.
- WouterGevaert, GeorgiTsenov, ValeriMladenov, Neural networks used for speech recognition, Journal of Automatic Control, University ofBelgrade, Vol. 20:1-7, 2010
- Austin Marshall, Artificial neural network for speech recognition, March 3, 2005, 2nd annual student research showcase
- Christopher M. Bishop, Neural network for pattern recognition, Clarendon Press, Oxford, 1995.
|