International Journal of Innovative Research in Science, Engineering and Technology

International Journal of Innovative Research in Science, Engineering and Technology

Menu

ISSN ONLINE(2319-8753)PRINT(2347-6710)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

MHD Heat and Mass Transfer Flow of a Viscoelastic Fluid Past an Impulsively Started Infinite Vertical Plate with Chemical reaction

1S Karunakar Reddy, 2D Chenna Kesavaiah and 1M N Raja Shekar
 1Department of Mathematics, College of Engineering, Nachupally, Jagityala, JNT University, Hyderabad, AP, India
2Department of H & BS, Visvesvaraya College of Engineering & Technology, Greater Hyderabad, A.P, India
1Department of Mathematics, College of Engineering, Nachupally, Jagityala, JNT University, Hyderabad, AP, India
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology

International Journal of Innovative Research in Science, Engineering and Technology

Abstract

The objective of the present study, we discuss the heat and mass transfer on MHD unsteady visco-elastic second order Rivlin-Erickson fluid past an impulsively started infinite vertical plate in the presence of a foreign mass and constant mass flux on taking into account of viscous dissipative heat at the plate under the influence of a uniform transverse magnetic field in the presence of chemical reaction. The flow is governed by a coupled non-linear system of partial differential equations. These equations are solved by using perturbation technique. The velocity, temperature, concentration, skin - friction and the rate of heat transfer are derived. The results are graphically discussed for various values of physical parameters

Keywords
Chemical reaction, Rivlin - Erickson Fluid, Mass Transfer, heat source, Porous medium, MHD Viscous Flow, mass flux

INTRODUCTION
In recent years, a great deal of interest has been generated in the area of heat and mass transfer of the boundary layer flow over a stretching sheet, in view of its numerous and wide-ranging applications in various fields like polymer processing industry in particular in manufacturing process of artificial film and artificial fibers and in some applications of dilute polymer solution. Heat and mass transfer in wet porous media are coupled in a complicated way. The structure of the solid matrix varies widely in shape. There is, in general, a distribution of void sizes, and the structures may also be locally irregular. Energy transport in such a medium occurs by conduction in all of the phases. Mass transport occurs within voids of the medium. In an unsaturated state these voids are partially filled with a liquid, whereas the rest of the voids contain some gas.
It is a common misapprehension that nonhygroscopic fibers (i.e., those of low intrinsic for moisture vapor) will automatically produce a hydrophobic fabric. The major significance of the fine geometry of a textile structure in contributing to resistance to water penetration can be stated in the following manner.
In recent years, a great deal of interest has been generated in the area of heat and mass transfer of the boundary layer flow over a stretching sheet, in view of its numerous and wide-ranging applications in various fields like polymer processing industry in particular in manufacturing process of artificial film and artificial fibers and in some applications of dilute polymer solution. Engineering processes in which a fluid supports an exothermal chemical or nuclear reaction are very common today and the correct process design requires accurate correlation for the heat transfer coefficients at the boundary surfaces. Despite its increasing importance in technological and physical problems, the unsteady MHD free convection flows of dissipative fluids past an infinite plate have received much attention because of non-linearity of the governing equations. Saravana et.al [20] Mass Transfer effects on MHD Viscous flow past an impulsively started infinite vertical plate with constant mass flux. The effect of the presence of impurities is studied in scientific literature by considering it as a foreign mass. It is usually a very complicated phenomenon; however, by introducing suitable assumptions, the governing equations can be simplified. Rajput and Kumar [12] Radiation effects on MHD flow past an impulsively started vertical plate with variable heat and mass transfer.
In view of increasing importance of non-Newtonian flows, a great deal of work has been carried out to find the similarity solution of viscoelastic fluid flow over impervious stretching boundary. Rajagopal et al. [21] examined for a special class of visco-elastic fluids known as second order fluids. Siddappa et al. [22] studied the flow of visoelastic fluids of the type Walter’s liquid B past a stretching sheet. Abel and Veena [23] studied the visco -elasticity on the flow and heat transfer in a porous medium over a stretching sheet. All these studies deals with the studies concerning non- Newtonian flows and heat transfer in the absence of magnetic fields, but present years we find several industrial applications such as polymer technology and metallurgy where the magnetic field is applied in the visco-elastic fluid flow. Sarpakaya [25] was mostly first researcher to investigate MHD flows of non-Newtonian fluids. Andersson [26] investigated the flow problem of electrically conducting viscoelastic fluid past a flat and impermeable elastic sheet and later his work is extended by many authors Abel, et.al; Abel et.al ; Seddeek and Prasad et.al [27, 28, 29, 5]. Abel and Mahesha [30] Heat Transfer in MHD Viscoelastic Fluid Flow over a Stretching Sheet with Variable Thermal Conductivity, Non-Uniform Heat Source and Radiation.
Chemical reactions usually accompany a large amount of exothermic and endothermic reactions. These characteristics can be easily seen in a lot of industrial processes. Recently, it has been realized that it is not always permissible to neglect the convection effects in porous constructed chemical reactors. The reaction produced in a porous medium was extraordinarily in common, such as the topic of PEM fuel cells modules and the polluted underground water because of discharging the toxic substance, etc. Muthucumaraswamy and Ganesan [11] studied effect of the chemical reaction and injection on flow characteristics in an unsteady upward motion of an isothermal plate. Deka et al. [3] studied the effect of the first order homogeneous chemical reaction on the process of an unsteady flow past an infinite vertical plate with a constant heat and mass transfer. Chamkha [1] assumed that the plate is embedded in a uniform porous medium and moves with a constant velocity in the flow direction in the presence of a transverse magnetic field. Kesavaiah et.al [9] effects of the chemical reaction and radiation absorption on an unsteady MHD convective heat and mass transfer flow past a semi-infinite vertical permeable moving plate embedded in a porous medium with heat source and suction. Modather et.al [10] An analytical study of MHD heat and mass transfer oscillatory flow of a micropolar fluid over a vertical permeable plate in a porous medium. Kandasamy et al. [8] studied the nonlinear MHD flow, with heat and mass transfer characteristics, of an incompressible, viscous, electrically conducting, Boussinesq fluid on a vertical stretching surface with chemical reaction and thermal stratification effects. Devika et.al [31] MHD oscillatory flow of a visco elastic fluid in a porous channel with chemical reaction.
In most of the studies mentioned above, viscous dissipation is neglected. Soundalgekar [14] analyzed viscous dissipative heat on the two-dimensional unsteady free convective flow past an infinite vertical porous plate when the temperature oscillates in time and there is constant suction at the plate. Satyanarayana et.al [13] viscous dissipation and thermal radiation effects on an unsteady MHD convection flow past a semi-infinite vertical permeable moving porous plate. Raja Shekar and Karunakar Reddy [15] Heat and Mass Transfer past a Continuously Moving Porous Boundary in the Presence of a Magnetic Field. Chakrabarti and Gupta [24] Hydromagnetic Flow and Heat Transfer over a Stretching Sheet.
Study of MHD flow with heat and mass transfer plays an important role in biological Sciences. Effects of various parameters on human body can be studied and appropriate suggestions can be given to the persons working in hazardous areas having noticeable effects of magnetism and heat variation. Study of MHD flows also has many other important technological and geothermal applications. Some important applications are cooling of nuclear reactors, liquid metals fluid, power generation system and aero dynamics. The effects of radiation on free convection on the accelerated flow of a viscous incompressible fluid past an infinite vertical porous plate with suction has many important technological applications in the astrophysical, geophysical and engineering problem. Vajravelu and Sastri [18]. Gupta et al. [6] have analyzed free convection effects on the flow past an accelerated vertical plate in an incompressible dissipative fluid. Mass transfer effects on the flow past an exponentially accelerated vertical plate with constant heat flux was studied by Jha et al [7]. Das et al. [2] have studied effects of mass transfer on flow past an impulsively started vertical infinite plate with constant heat flux and chemical reaction. Ezzat Magdy [4] have considered magneto hydrodynamic unsteady flow of non- Newtonian fluid past an infinite porous plate. Takhar et al.[17] have studied radiation effects on MHD free convection flow of a radiating gas past a semi- infinite vertical plate. Non - Darcy convective boundary layer flow past a semi-infinite vertical plate in saturated porous media was studied by Takhar and Beg [16]. Saleh Alharbi et.al [19] Heat and mass transfer in MHD Visco-Elastic fluid flow through a porous medium over a stretching sheet with chemical reaction.
The objective of the present paper is to analyze the heat and mass transfer effects on MHD visco elastic fluid flow past an impulsively started infinite vertical plate with constant mass flux, on taking into account of viscous dissipative heat under the influence of a uniform transverse magnetic field with heat source in the presence of chemical reaction.

II. FORMULATION OF THE PROBLEM
Consider the flow of a viscous incompressible visco-elastic second order Rivlin-Erickson fluid past an impulsively started infinite vertical plate with heat source in the presence of chemical reaction taking into an account. The x – axis is taken along the plate in the vertically upward direction and the yx - axis is chosen normal to the plate. Initially the temperature of the plate and the fluid T , and the species concentration at the plate w C and in the fluid throughout C are assumed to be the same. At time t 0, the plate temperature is changed to w T causing convection currents to flow near the plate and mass is supplied at a constant rate to the plate and the plate starts moving upward due to impulsive motion, gaining a velocity of 0 U . A uniform magnetic field of intensity 0 H is applied in the y-direction. Therefore the velocity and the magnetic field are given by q = (u,0,0) and ( ) 0 H = 0,H ,0 The flow being slightly conducting the magnetic Reynolds number is much less than unity and hence the induced magnetic field can be neglected in comparison with the applied magnetic field (Sparrow and Cess [22]) in the absence of any input electric field, the flow is governed by the following equations:
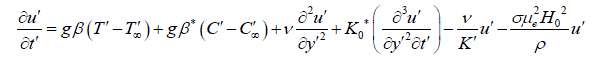image (1)
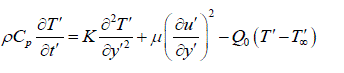image (2)
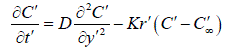image (3)
The initial and boundary conditions for the velocity, temperature and concentration fields are
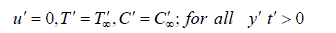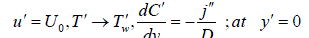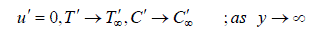image
image
image (4)
Where u is the velocity of the fluid along the plate in the x - direction, t is the time, g is the acceleration due to gravity, is the coefficient of volume expansion, is the coefficient of thermal expansion with concentration, T is the temperature of the fluid near the plate, w T is the temperature of the fluid far away from the plate, w T is the temperature of the fluid, C is the species concentration in the fluid near the plate, C is the species concentration in the fluid far away from the plate, j is the mass flux per unit area at the plate, is the kinematic viscosity, 0 K is the coefficient of kinematic visco-elastic parameter, is the electrical conductivity of the fluid, e is the magnetic permeability, 0 H is the strength of applied magnetic field, is the density of the fluid, p C is the specific heat at constant pressure, K is the thermal conductivity of the fluid, is the viscosity of the fluid, D is the molecular diffusivity, 0 U is the velocity of the plate. Equations (1) - (3) can be made dimensionless by introducing the following dimensionless variables and parameters: In order to write the governing equations and the boundary conditions in dimensionless from, the following nondimensional quantities are introduced.
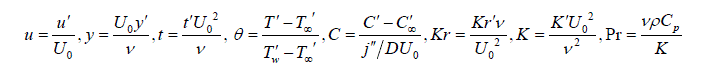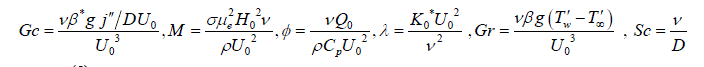image
image (5)
where Gr is the thermal Grashof number, Gc is modified Grashof Number, Pr is Prandtl Number, M is the magnetic field, Sc is Schmdit number, Kr is Chemical Reaction, K is Porous Permeability,  is Heat source parameter respectively.
In terms of the above dimensionless quantities, Equations (1) - (2) reduces to
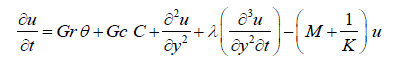image (6)
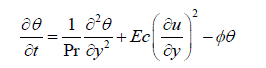image (7)
image (8)
The corresponding boundary conditions are
image (9)

III. SOLUTION OF THE PROBLEM
Equation (6) – (8) are coupled, non – linear partial differential equations and these cannot be solved in closed – form using the initial and boundary conditions (9). However, these equations can be reduced to a set of ordinary differential equations, which can be solved analytically. This can be done by representing the velocity, temperature and concentration of the fluid in the neighbourhood of the fluid in the neighbourhood of the plate as
image (10)
Substituting (10) in Equation (6) – (8) and equating the harmonic and non – harmonic terms, and neglecting the higher order terms of ( ) 2 0 , we obtain
image (11)
image (12)
image (13)
image (14)
image (15)
image (16)
The corresponding boundary conditions can be written as
image (17)
The Equations (11) - (16) are still coupled and non-linear, whose exact solutions are not possible. So we expand image in terms i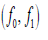mage of Ec in the following form, as the Eckert number is very small for incompressible flows.
image (18)
Substituting (18) in Equations (11) - (16), equating the coefficients of Ec to zero and neglecting the terms in Ec2 and higher order, we get the following equations.
image       (19)
image      (20)
image      (21)
image      (22)
image      (23)
image      (24)
image      (25)
image      (26)
image      (27)
image      (28)
image      (29)
image      (30)
The respective boundary conditions are
image (31)
image (32)
Solving Equations (19) - (30) under the boundary conditions (31) and (32) we obtain the velocity, temperature and concentration distributions in the boundary layer as
image
image
Skin-friction:
We now calculate Skin-friction from the velocity field. It is given in non-dimensional form as:
image
image
Rate of heat transfer: The dimensionless rate of heat transfer is given by
image
Sherwood number: The dimensionless Sherwood number is given by
image

IV. RESULTS AND DISCUSSION
From figure (1), we observe that the velocity distribution (u) is drawn against y for different values of magnetic parameter (M) for visco-elastic parameter λ 0.1 and Prandtl number (Pr ) = 0.71 (air). We notice that the velocity distribution (u) decreases with the increase in (M) . From figure (2) velocity distribution (u) for viscoelastic parameter λ = 0.1 is drawn against y for different values of Grashof numberGr . We notice that the (u) increases as Gr increases. From figure (3), velocity distribution (u) is drawn against y for different values of viscoelastic parameter λ . Here velocity distribution (u) increases with the increase of λ . Figures (4) and (5) represents the distribution (u) is drawn against y for different values of Schmidt number (Sc ) and Eckert number (Ec) . We observe that velocity distribution (u) is decrease with increase in Sc and Ec . Figures (6) and (7) represents the distribution (u) is drawn against y for different values of porous permeability parameter (K ) and Chemical reaction parameter (Kr) . We observe that velocity distribution (u) is increase with increase in K , where as decrease with increase Kr Figures (8) - (14) is drawn for Temperature distribution (θ) against y for different values of Eckert number (Ec) , Grashof number (Gr) , Porous permeability parameter (K) , Chemical reaction parameter (Kr) , Magnetic parameter (M) , heat source parameter (u ) and Schmidt number (Sc) . Here we observed that the Temperature distribution (u ) increases with Eckert number (Ec) and heat source parameter increases, where as the reverse effect noticed with increase inGr,K,Kr,M and Sc . From Figures (15) and (16) we observe that an increase in Kr and Sc leads to decrease in the Concentration profiles (C) . Figure (17) is drawn for Skin-friction (u ) at λ = 0.1is drawn against magnetic parameter (M) from this figure we observe that u decreases with the increase of Kr for Pr=0.71. Figure (18) shows that Nusselt number (Nu) versus Prandtl number (Pr) for different values of Grashof number (Gr) . We observe that Nusselt number (Nu) at λ = 0.1increases with the increase of Gr
APPENDIX
image

V. CONCLUSION
The objective of the present study, we discuss the heat and mass transfer on MHD unsteady visco- elastic second order Rivlin-Erickson fluid past an impulsively started infinite vertical plate in the presence of a foreign mass and constant mass flux on taking into account of viscous dissipative heat at the plate under the influence of a uniform transverse magnetic field in the presence of chemical reaction. The resulting partial differential equations are transformed into a set of ordinary differential equation using normalisation and solved in closed-form. Numerical evaluations of the closed- form results are performed and graphical results are obtained to illustrate the details of the flow and heat and mass transfer characteristics and their dependence on some physical parameter. It is observed that the velocity profile is increasing with increasing slip parameter, Grashof number, viscoelastic parameter and permeability of porous medium. Also, velocity reducing with decreasing magnetic parameter, Schmidt number, Eckert number and chemical reaction parameter. The fluid temperature is reduced by increases in the values of the Grashof number, porous permeability, chemical reaction, magnetic parameter and Schmidt number, but the temperature increasing with increasing values Eckert number, heat source parameter. Concentration is reducing with increase in Schmidt number and chemical reaction parameter. In addition, it is found that skin friction coefficient decreases with chemical reaction parameter. However, the Nusselt number increases with an increase in Grashof number.

Figures at a glance
Figure Figure Figure Figure Figure
Figure 1 Figure 2 Figure 3 Figure 4 Figure 5


Figure Figure Figure Figure Figure
Figure 6 Figure 7 Figure 8 Figure 9 Figure 10


Figure Figure Figure Figure Figure
Figure 11 Figure 12 Figure 13 Figure 14 Figure 15


Figure Figure Figure
Figure 16 Figure 17 Figure 18
 

References
  1. A. J. Chamkha (2004): Unsteady MHD convective heat and mass transfer past a semi-vertical permeable moving plate with heat absorption. Int. J. Eng., Sci., 42: pp. 217-230.
  2. U.N. Das, R. K. Deka and V. M. Soundalgekar (1994): Effects of mass transfer on flow past an impulsively started vertical infinite vertical plate with constant heat flux and chemical reaction. Forschung in Ingenieurwesen 60, pp. 284 – 287
  3. R. Deka U. N. Das and V. M. Soundalgekar (1994): Effect of mass transfer on flow past impulsively started infinite vertical plate with a constant heat flux and chemical reaction. Forschung im ingenieurwesen; 60: pp. 284-287.
  4. A. Ezzat Magdy (1994). Magnetohydrodynamic unsteady flow of non- Newtonian fluid past an infinite porous plate. Indian J. pure appl. math. 25(6), pp. 655 - 664.
  5. K. V. Prasad , D. Pal, V. Umesh and N. S. Prasanna Rao (2010): The Effect of Variable Viscosity on MHD Viscoelastic Fluid Flow and Heat Transfer over a Stretching Sheet,” Communications in Nonlinear Science and Numerical Simulation, Vol. 15, No. 2, February 2010, pp. 331- 344.
  6. A. S. Gupta, I. Pop and V. M. Soundalgekar (1979): Free convection effects on the flow past an accelerated vertical plate in an incompressible dissipative fluid. Rev. Roum. Sci. Techn. -Mec.Apl. 24, pp. 561 - 568.
  7. B. K. Jha, R. Prasad and S. Rai (1991): Mass transfer effects on the flow past an exponentially accelerated vertical plate with constant heat flux. Astrophysics and Space Science 181, pp. 125- 134.
  8. R. Kandasamy, K. Periasamy and K. K. Sivagnana Prabhu (2005): Chemical Reaction, Heat and Mass Transfer on MHD Flow over a Vertical Stretching Surface with Heat Source and Thermal Stratification Effects”, Int. J. of Heat and Mass Transfer, 48, 4557
  9. D. Ch. Kesavaiah, P. V. Satyanarayana and S. Venkataramana (2011): Effects of the chemical reaction and radiation absorption on an unsteady MHD convective heat and mass transfer flow past a semi-infinite vertical permeable moving plate embedded in a porous medium with heat source and suction Int. J. of Appl. Math and Mech. 7 (1): pp. 52-69
  10. M. Modather, A. M. Rashad, and A. J. Chamkha (2009): An analytical study of MHD heat and mass transfer oscillatory flow of a micropolar fluid over a vertical permeable plate in a porous medium, Turkish J. Eng. Env. Sci. 33, pp. 1 – 13.
  11. R. Muthucumaraswamy and P. Ganesan (2001): Effect of the chemical reaction and injection on flow characteristics in an unsteady upward motion of an isothermal plate, J. App., Mech., Tech ., Phys., 42: pp. 665-671
  12. U. S. Rajput and S. Kumar (2012): Radiation effects on MHD flow past an impulsively started vertical plate with variable heat and mass transfer, Int. J. of Appl. Math. and Mech. 8(1): 66-85, 2012.
  13. P. V. Satyanarayana, D. Ch. Kesavaiah and S. Venkataramana (2011): Viscous dissipation and thermal radiation effects on an unsteady MHD convection flow past a semi-infinite vertical permeable moving porous plate. International Journal of Mathematical Archive-2(4), pp. 476-487
  14. V. M. Soundalgekar (1972): Viscous dissipation effects on unsteady free convective flow past an infinite, vertical porous plate with constant suction, Int. J. Heat Mass Transfer, 15: pp.1253-1261
  15. M. N. Raja Shekar and S. Karunakar Reddy (2012): Heat and Mass Transfer past a Continuously Moving Porous Boundary in the Presence of a Magnetic Field, International Journal of Computer Applications, Volume 39– No.12, 2012, pp.13-16
  16. H. S. Takhar and O. A. Beg (1996): Non - Darcy convective boundary layer flow past a semi- infinite vertical plate in saturated porous media. Heat Mass Transfer 32, pp. 33 – 44.
  17. H. S. Takhar, R. S. Gorla and V. M. Soundalgekar (1996). Radiation effects on MHD free convection flow of a radiating gas past a semiinfinite vertical plate. Int. J. Numerical Methods Heat Fluid Flow 6, pp. 77 - 83.
  18. K. Vajravelu and K. S. Sastri (1977): Correction to ‘Free convection effects on the oscillatory flow an infinite, vertical porous, plate with constant suction, I. Proc. R. Soc. A 353, pp. 221 - 223.
  19. M. Saleh, Alharbi, A. A. Mohamed S. Bazid, Mahmoud El Gendy (2010): Heat and Mass Transfer in MHD Visco-Elastic Fluid Flow through a Porous Medium over a Stretching Sheet with Chemical Reaction, Applied Mathematics, 1, pp. 446-455
  20. R. Saravana, S. Sreekanth, S. Sreenadh, R. Hemadri Reddy (2011): Mass Transfer effects on MHD Viscous flow past an impulsively started infinite vertical plate with constant mass flux, Advances in Applied Science Research, 2 (1): pp. 221-229
  21. K. R. Rajagopal, T. Y. Na and A. S. Gupta (1984): Flow of Visco-Elastic Fluid over a Stretching Sheet, Rheol Acta, Vol. 23, pp. 213-215.
  22. B. Siddappa and S. Abel (1985): Non-Newtonian flow past a stretching plate, Zeitschrift für Angewandte Mathematik und Physik (ZAMP), Vol. 36, pp. 890-892.
  23. S. Abel and P. H. Veena (1998): Visco-Elastic Fluid Flow and Heat Transfer in Porous Medium over a Stretching Sheet, International Journal of Non-Linear Mechanics, Vol. 33, pp. 531-540.
  24. A. Chakrabarti and A. S. Gupta (1979): Hydromagnetic Flow and Heat Transfer over a Stretching Sheet, Quarterly Journal of Mechanics and Applied Mathematics, Vol. 37, pp. 73-78.
  25. T. Sarpakaya (1961): Flow of Non-Newtonian Fluids in Magnetic Field, AICHE Journal, Vol. 7, pp. 324-328.
  26. H.I. Andersson (1992): MHD Flow of Viscoelastic Fluid past a Stretching Surface, Acta Mechanica, Vol. 95, pp. 227- 230.
  27. S. Abel, A. Joshi and R. M. Sonth R M (2001):, Heat Transfer in a MHD Visco-Elastic Fluid over a Stretching Surface, Journal of Applied Mathematics and Mechanics, Vol. 81, pp. 691-698.
  28. S. Abel, P.H. Veena, K. Rajgopal and V. K. Pravin (2004): Non-Newtonian Magneto Hydrodynamic Flow over a Stretching Surface with Heat and Mass Transfer, International Journal of Non-Linear Mechanics, Vol. 39, pp. 1067-1078.
  29. M. A. Seddeek (2007): Heat and Mass Transfer on a Stretching Sheet with a Magnetic Field in a Visco-Elastic Fluid Flow through a Porous Medium with Heat Source or Sink, Computational Materials Science, Vol. 38, pp. 781-787.
  30. S. Abel and N. Mahesha (2008): Heat Transfer in MHD Viscoelastic Fluid Flow over a Stretching Sheet with Variable Thermal Conductivity, Non-Uniform Heat Source and Radiation, Applied Mathematical Modelling, Vol. 32, pp. 1965-1983.
  31. B. Devika et.al (2013): MHD oscillatory flow of a visco elastic fluid in a porous channel with chemical reaction. International Journal of Engineering Science Invention, Vol. 2(2), pp.2-35.