Research and Reviews - International Journals

International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Menu

ISSN ONLINE(2278-8875) PRINT (2320-3765)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

MIMO Discrete Wavelet Transform for the Next Generation Wireless Systems

Rameez Asif1, Tahereh S. Ghazaany2, Raed. A. Abd-Alhameed3, James M. Noras4, Steven M. R. Jones5, Jonathan Rodriguez6 and Chan H. See7
  1. Communications Research Group, School of Engineering, Design and Technology, University of Bradford, Bradford, BD7 1DP, United Kingdom
  2. Communications Research Group, School of Engineering, Design and Technology, University of Bradford, Bradford, BD7 1DP, United Kingdom
  3. Communications Research Group, School of Engineering, Design and Technology, University of Bradford, Bradford, BD7 1DP, United Kingdom
  4. Communications Research Group, School of Engineering, Design and Technology, University of Bradford, Bradford, BD7 1DP, United Kingdom
  5. Communications Research Group, School of Engineering, Design and Technology, University of Bradford, Bradford, BD7 1DP, United Kingdom
  6. Communications Research Group, School of Engineering, Design and Technology, University of Bradford, Bradford, BD7 1DP, United Kingdom
  7. Communications Research Group, School of Engineering, Design and Technology, University of Bradford, Bradford, BD7 1DP, United Kingdom
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Abstract

Study is presented into the performance of Fast Fourier Transform (FFT) and Discrete Wavelet Transform (DWT) and MIMO-DWT with transmit beamforming. Feedback loop has been used between the equalizer at the transmitter to the receiver which provided the channel state information which was then used to construct a steering matrix for the transmission sequence such that the received signals at the transmitter can be combined constructively in order to provide a reliable and improved system for next generation wireless systems. As convolution in time domain equals multiplication in frequency domain no such counterpart exist for the symbols in space, means linear convolution and Intersymbol Interference (ISI) generation so both zero forcing (ZF) and minimum mean squared error (MMSE) equalizations have been employed. The results show superior performance improvement and in addition allow keeping the processing, power and implementation cost at the transmitter which has less constraints and the results also show that both equalization algorithms perform alike in wavelets and the ISI is spread equally between different wavelet domains.

Keywords
Multiple-Inputs Multiple-Outputs (MIMO), Beamforming, Discrete Wavelet Transform (DWT), Zero Forcing (ZF), Intersymbol Interference (ISI), Minimum Mean Squared Error (MMSE)
 
 

INTRODUCTION
In the world of communication any problem within the communication system is usually divided into two main parts, i.e. source coding and channel coding. In a number of ways it can be assumed that these techniques are interrelated which provides us with some very important algorithms and techniques that can then be employed to solve these problems. When the word source coding is used it usually refers to the idea that some type of discrete representation of the data is sorted so as to reduce the redundancy that is present in the transmission sequence, but on the other hand the channel coding defines the distortion that is brought into the discrete transmission scheme, in order to minimize the channels distorting effects on the symbols. There are many different techniques present in the literature for channel coding but the best performance is only achieved if the channel through which the data stream has to travel is known and this information can be attained from the equalizer at the receiver by using a closed loop to the transmitter.
With the continuous increase in the demand of high performance systems for multiple classes of traffic researchers have proposed that replacing the conventional Fourier based OFDM [1-6] system with the filter bank based multirate wavelet transform can provide some extra advantages like that of multiresolution analysis, which allows the signal to be studied in space, or time – frequency domain, another major contribution of the wavelet transform is that it is more spectrally efficient because the input data stream is divided into approximate and detailed coefficients providing the 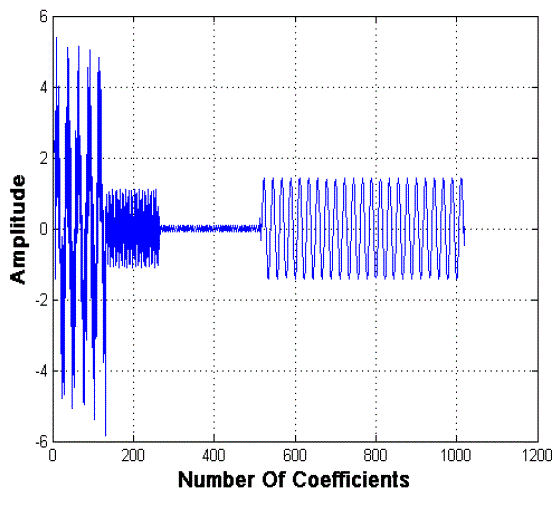land and groves of the transmission sequence as shown in Fig. 1 for a sum of sinusoidal waves. Now this concept closely follows the OFDM transmission structure where the transmitted sequence is divided into a number of sub carriers but they are orthogonal to each other, and the orthogonality is sometimes severely damaged by the multipath [7] which will make these subcarriers overlap causing ICI and making it hard for the equalizer to decide what was the real transmission sequence, which then requires for the guard band to be inserted to separate the symbols in time so they do not overlap making the scheme suitable for multipath transmission. Then there is another problem with the FFT and that is of leakage causing inter symbol interference, but in the case of wavelets which provides groves as the approximate coefficients and lands as detailed just like in a rifling process even if the grove is damaged it can still be easily differentiated from the land and no guard band insertion is required and the leakage in wavelets is almost negligible and the main energy is concentrated in the main lobe which make this transform a perfect choice for any type of unreliable channels. Symbol orthogonality is maintained using the perfect reconstruction quadrature mirror filter bank which consist of half band low pass and half band high pass filters on one end of the transmission system and the conjugate mirrored filters on the other end.
This transform also has the advantage that the signal is divided into its individual components and every component is assigned a different frequency band in the frequency spectrum which results in reduced computational complexity as compared to the division into individual sinusoids as in Fourier transform from O(Nlog2N) to O(N) [8].
The bases functions for wavelet transform can be localized in space using the multi-resolution analysis [9] and the harmonics can be very easily distinguished.
Another way of increasing the reliability and to increase the transmitted or received data rates is to employ Multiple Input Multiple Output systems as they can be used to take advantage of the spatial diversity or time diversity by creating multiple channels in space without using any additional bandwidth [10]. The main reason behind the success of the MIMO systems is the same that they are more spectrally efficient and less transmission power is required to match a given throughput at a certain BER level as compared to the SISO systems [11]. In [12] WPM Multicode CDMA system performance was compared against the conventional Multicode CDMA system. In [13] again performance of WPM-MIMO in AWGN was studied and it was shown that the WMCM systems perform better and MIMO systems enhance system performance in AWGN channel.
A new wavelet based system has been presented that uses the time-frequency localization of the wavelet transform and also the transmit diversity technique in conjunction with beamforming to achieve high rate data transmission and reliability for the next generation wireless systems (NGWS). The performance of two different equalization techniques has been considered as there is no convolution counterpart available for the symbols present in wavelet domain which can give rise to ISI. The study was done using Rayleigh multipath fading channel and AWGN.
The rest of this paper is divided as follows. Section II introduces the concept of wavelet analysis and perfect reconstruction, Section III details the system model, Section IV deals with the error probability, followed by the discussion on the simulation results in Section V and the conclusion is presented in section VI.

II. INTRODUCTION TO WAVELET ANALYSIS
Signals can be decomposed into their constituent components each corresponding to different scales each within a different frequency range using the wavelets transform allowing the signal to be studied much more efficiently by changing the scale of the frequency for a particular component of interest.
Wavelets as the name suggests are wave like oscillations which quickly decay and are used to represent the mother function or the mother wavelet from which the daughter wavelets are generated and are in reality just the scaled and translated replicas [10]. There are infinite sets of basis fuctions available for the wavelets and any one of them can be employed for the signal study making it different from any other known method of signal analysis.
The continuous wavelet transform can be mathematically defined as [10]:
where "x" represents the scaling factor, "z" is the shifting parameter and “ψx,z t " denotes the mother wavelet. In its continuous form the data carries redundant information and the transform will require extensive analytical calculation for which we then sought the discrete representation in order to be able to devise a viable inverse transform function for the practical employability of the technique.
The discretized mother wavelet will be of the form:
The product of any random signal s[n] with the scaling and wavelet function provides us with the desired DWT [10] as shown here after.
Where, φ t represents the scaling function and ψ(t) is the wavelet function. These functions are discretized values at a (a = 1,2 … ,m) and at translation b (1,2 … . , t). The filters of the perfect reconstruction quadrature mirror filter bank (PR-QMF) that are used to implement the DWT consisting of half band high pass g(b) and half band low pass h(b) filters in a multicarrier modulation system follow the relationship as in (7) if the impulse response of one filter is known the rest can easily be calculated using (7);
And these filters must satisfy the condition
The resultant approximate and detailed coefficients obtained for the DWT are of the form;
The shifting and translation of the wavelet signal causes a delay within composite symbols by a factor „ α‟ in accordance to the z-transform relation (X z = n x m z−α, where z−α = e−jαw) and requires adjacent matched filters to perfectly reconstruct the signal. This condition can be represented mathematically as [14].

III. SYSTEM MODEL
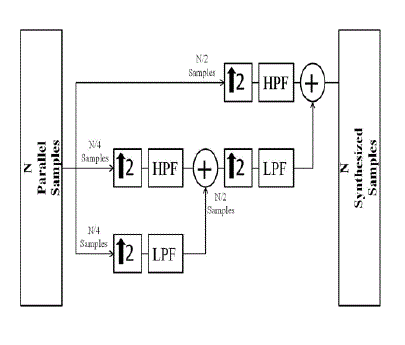
A general representation of the system model is presented in the Fig 1., where the discretized and modulated bit stream is first converted from serial to parallel and then passed through the synthesis filter bank. There is a trade off present between the levels of synthesis and decomposition that are employed and the system latency which can be optimized according to the application requirement or the channel requirements. Before the parallel symbol streams pass through the filters within the filter bank they are upconverted which increases the signal resolution in order to provide a very detailed description of the signal and to provide a more accurate approximation. After the required N level of synthesizing the synthesized wavelet symbol is then propagated through the multipath fading channel using the transmission scheme. At the receiver the received signal is equalized to remove any unwanted channel effects and then passed to the analysis filter bank where it is decomposed and down sampled and the channel state information is also sent to the transmitter to adjust the next transmission sequence according to the channel conditions.
A. DWT in Transmitter
In a multicarrier system unlike image processing the inverse wavelet transform is applied at the transmitter in order to synthesize the transmission sequence as shown in Fig. 2a., using the PRQMF. This convolution between the symbols and the filters can be mathematically described as;
The process of IDWT is also referred to as a Synthesis Process. This synthesized signal then propagates through the Rayleigh multipath fading channel in the presence of noise. For greater understanding of the process of convolution of the wavelet symbols and the channel please refer to authors [1].
B. DWT signal in Multipath Rayleigh Channel and AWGN
When the signal is propagated through the channel it suffers the phase and amplitude distortions due to fading, either its flat fading or frequency selective fading. In addition to these changes in a multipath environment reflection and diffraction effects cause many multiple time delayed copies of the signal to arrive at the receiver which if combined destructively will lose all the information. The effects caused by the multipath channel can be summarized in a mathematical form as;
The amplitude change and the time delay of the signals travelling through the channel in (12) are represented by am t, τ , and τm is the phase shift for the mth multipath at the time instance t. Multipath summation limits are from 1 to M with Dirac delta δ • .
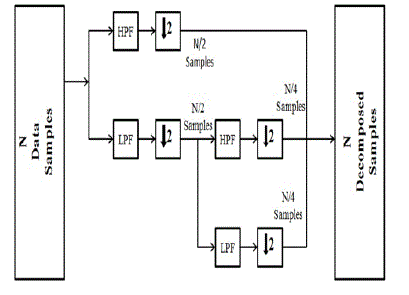
C. DWT in Receiver
The received signal after equalization is passed through the conjugate LPF h*(-b) and HPF g*(-b). The signal gets decomposed within analysis filter bank into its constituent approximate and detailed coefficients and then downsampled to further reduce the redundancy by a factor of 2. The process is repeated again until the desired N data streams are successfully retrieved. These parallel streams are then converted back to the serial using serial to parallel converter and then demapped.

IV. ERROR PROBABILITY
The instantaneous error probability in the presence of AWGN for lucid detection can be stated in the form of mathematical expression as:
In order to improve instantaneous error probability beamforming can be applied which will align the phases of two different incoming signals at the receiver in order for constructive combination of both the incoming signal streams in order to achieve high diversity gain, because otherwise the signals transmitted through the different antenna elements will travel through two separate Rayleigh multipath channel and can only provide SISO like performance due to the phase difference of the received waveforms at the receiver. Mathematically the implementation of this technique can be realized as;
If „s‟ is the transmitted symbol, „h‟ is the channel impulse response then;
The addition of the AWGN by the channel is represented as n. For a transmit diversity system having two transmit antennas (14) can be modified as where instead of one we have two separate channels
Let us assume that the channel estimator feedback loop has provided us with the CSI and the channel phases are ejφ1 and ejφ2 respectively. Them (15) can be further modified to add this information and the steering matrix can be calculated.
As a result of the channel knowledge and the steering matrix we can successfully constructively combine both incoming signal streams to achieve maximum diversity gain.

V. SIMULATION RESULTS AND DISCUSSION
All the simulations have been carried out using Monte Carlo simulations. Table (1) summarizes the basic parameters that have been used for the experiment.
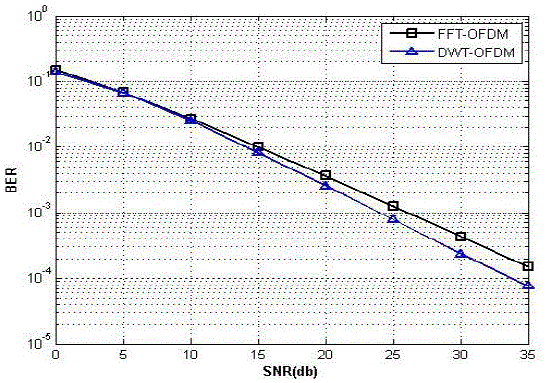
The first part of the performance study was done to verify the theory that states that wavelet transform will outperform the conventional OFDM system as it is an industry standard and widely accepted but as can be seen in Fig. 4 that at the BER around 10-4 region discrete wavelet transform is providing about a 3dB gain out of which 1dB can be associated to the removal of CP making the transform spectrally efficient and another 2dB gain which proves that the idea of using filter banks based waveforms is quite attractive as the coefficients carrying the information has the information divided in such a way between approximation and detail parts that even after the degrading effects of the multipath channel and the ISI caused by the linear convolution of the synthesized wavelet symbol and channel the data was still recovered with less errors.
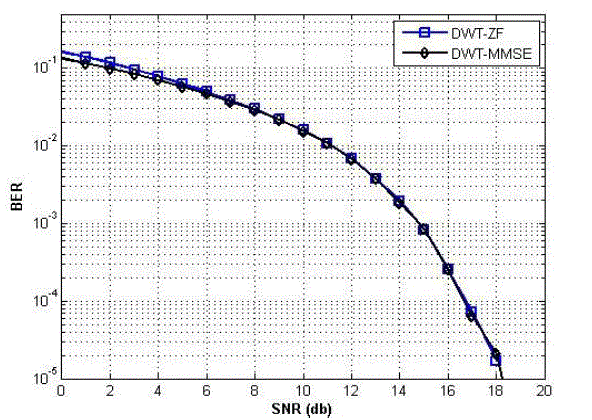
The next important question that comes to mind is that can this gain be increased by utilizing some other type of equalization method, but as can be seen in Fig. 5 that both the ZF and MMSE equalization algorithms performed alike, ZF gives rise to extra noise and MMSE has extra ISI which is spread on different wavelet domains that is why equalization of wavelets is still challenging, even though these two algorithms show performance difference when employed in FFT-OFDM systems.
In order to further enhance the capability of the system MIMO was employed but in a special way by incorporating the forward error correction by making use of the CSI and the results showed an outstanding performance difference, between just 2 transmit 1 receive antenna‟s and when the signal streams are steered using the matrix calculated according to the channel phase knowledge as can be seen in Fig. 5. Another important thing to note here is that the performance of Biorthogonal and Reverse Biorthogonal differs even within the same comparison parameters because of different reconstruction properties, for more detail on the subject of wavelets user is referred to [9].

VI. CONCLUSION
It can be concluded from the results produced that wavelet transform is indeed a better scheme for the multicarrier modulated systems and also for any type of unreliable channels because of its effectiveness in multipath environments. It is also concluded that the guard band saving which typically depend on the system design and wastes bandwidth can be saved using wavelet transform. Furthermore the proposed use of the FEC in the DWT-MIMO systems showed remarkable performance improvement and gain of about 18dB as compared to a simple two transmit and one receive antenna systems. Another thing that was seen in the results is that not all wavelet families perform alike which can form an interesting future contribution to get insight into the wavelet families and their behaviour and the optimal decomposition level and filter order.

ACKNOWLEDGMENT
This work has been performed in the framework of ARTEMOS project under work programme ENIAC JU 2010 and FCT (Fundação para a Ciência e Tecnologia).
The authors would also like to thank the support from Datong Plc. UK, under the KTP project No. 008734 with Bradford University.

Tables at a glance
Table icon
Table 1

Figures at a glance
Figure Figure Figure
Figure 1 Figure 2 Figure 3
Figure Figure Figure
Figure 4 Figure 5 Figure 6
 

References