Keywords
|
| Interacting system, Non-interacting system, IMC, IMC-PID, LabVIEW. |
INTRODUCTION
|
| Even though control theory has been developed significantly, the proportional- integral-derivative (PID) controllers are used for a wide range of process control, motor drives, magnetic and optic memories, automotive, flight control, instrumentation, etc. In industrial applications, PID type controllers were widely used.With its three-term functionality covering treatment to both transient and steady-state responses, proportional- integral-derivative (PID) control offers the simplest and yet most efficient solution to many real-world control problems. Since the invention of PID control in 1910 (largely owning to Elmer Sperry’s ship autopilot), and the Ziegler–Nichols’ (Z-N) straightforward tuning methods in 1942 [1], the popularity of PID control has grown tremendously. With advances in technology, the science of automatic control now offers a wide spectrum of choices for control schemes. However, most of industrial controllers were still implementing based around PID algorithms, particularly at lowest levels. This paper presents a [2] case study emphasizes building a mathematical model of a two tank fluid system, followed by system identification and parameter estimation, and finally designing a controller by pole placement. Model based control was developed primarily for processes having a pronounced time delay, the intent being to match the process delay with one in the control system. Model based control is very popular now adays due to the ability of such controllers to handle process with dead time effectively. Model-based control action is “intelligent” and helps in achieving uniformity, disturbance rejection, and set point tracking, all of which translate into better process economics One important type of model based control is Internal Model Control [IMC], which has the combined advantage of both open and closed systems[6]. It gives better performance in tracking the set point and load changes[3]. In [4], IMC design concept is extended to multi input-multi output discrete time systems. A good resource for IMC is [5]. |
| An excellent summary on PID tuning methods can be found in [6], [7], and [8]. However, no tuning method so far can replace the simple Z-N method for lower order systems in terms of familiarity and ease of use to start with. This work is based on real time model based control for the level control of a non-interacting and interacting three tank cylindrical tank system found to be second order with delay process .The process model is experimentally determined from step response analysis and it is interfaced to real time with LabVIEW. The controller settings of IMC, IMC PID and the conventional PID controller are analyzed, based on time domain specifications like peak time, overshoot and settling time. |
SYSTEM IDENTIFICATION
|
| A. Mathematical Modeling |
| To analyze the behavior of a process, a mathematical representation of the physical and chemical phenomenon taking place in it is essential and this representation constitutes the mathematical model. |
| B. Experimental Setup |
| The experimental set up shown in Figure 1 consists of water supply tank, pump, Plunger pump, level transmitter, pressure transmitter, Process tanks, Venturimeter, orifice meters with differential pressure transmitters, rotameter, pneumatic control valve, I/P converter, Pressure gauges. The pneumatic control valve is air to close, adjusts the flow of the water pumped to the cylindrical tank from the water reservoir. The level of the water in the tank is measured by means of the differential pressure transmitter and is transmitted in the form of (4-20) mA to the interfacing ADAM’s module to the Personal Computer (PC). |
| After computing the control algorithm in the PC control signal is transmitted to the I/P converter in the form of current signal (4-20) mA, which passes the air signal to the pneumatic control valve. The pneumatic control valve is actuated by this signal to produce the required flow of water in and out of the tank. There is a continuous flow of water in and out of the tank. The data acquisition system consists of 8 analog inputs and 4 analog outputs and also with 16 digital inputs and 16 outputs. It is voltage based data acquisition card. |
INTERNAL MODEL CONTROLLER
|
| A. The Imc Structure |
| The standard IMC structure is shown in Figure-2, where Gp(s), Gm(s), Gc(s), d(s) denote Process, Model, IMC Controller and Disturbance respectively. The internal model control principle states that control can be achieved only if the control system encapsulates, either implicitly or explicitly, some representation of the process to be controlled. Process model may not be invertible and the system is often affected by unknown disturbances [8]. From the schematic diagram figure 2 d(s) is an unknown disturbance; U(s) is the manipulated input is introduced to both the process and its model [11]. Y(s) is the process output is compared with the output of the model. |
| The closed loop transfer function for the IMC is, |
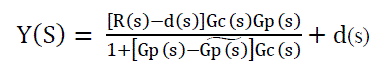 (1) (1) |
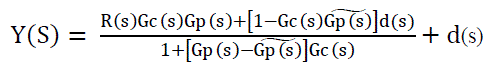 (2) (2) |
| To improve robustness, the effects of process model mismatch should be minimized. This mismatch usually occurs at the high frequency end of the system’s frequency response, a low-pass filter Gf(s) is usually added to attenuates the effects of mismatch[3]. The IMC is usually designed as the inverse of the process model in series with a low-pass filter, that is GIMC(s)=Gc (s) Gf(s). The resulting closed loop then becomes. |
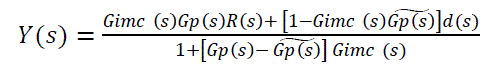 (3) (3) |
THREE TANK SYSTEM
|
| Tank1 is interacting with Tank2 and non-interacting with Tank3 is shown in figure 1. |
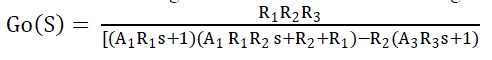 (4) (4) |
| The system identification of real time system can be obtained from the open loop method, for a given change in the input variable. At a fixed inlet flow rate, outlet flow rate, the system is allowed to reach the steady state. After that a step increment in the input flow rate is given, and various readings are noted till the process becomes stable in the tank. The transfer functions of tanks for interacting, non-interacting mode of 3 tank system are given below. |
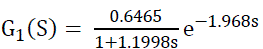 (5) (5) |
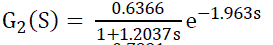 (6) (6) |
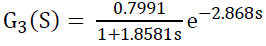 (7) (7) |
RESULT AND DISCUSSION
|
| The three tank level control system is studied under interacting and non-interacting mode. The obtained models were simulated and controller comparison i.e performance analysis of controller was studied from response curves are obtained using LabVIEW [10] Environment. |
CONCLUSION
|
| An analysis comes out with a conclusion that the peak time(tp) and overshoot(Mp) has got reduced drastically in IMC and IMC-PID when compared to conventional PID controller. The rise time(tr) of the system has improved and the settling time(ts) and integral square error (ISE) has got reduced in the case of IMC-PID compared to IMC and PID controller shown in table 2performance analysis. |
Tables at a glance
|
 |
 |
| Table 1 |
Table 2 |
|
Figures at a glance
|
 |
 |
 |
 |
| Figure 1 |
Figure 2 |
Figure 3 |
Figure 4 |
 |
 |
 |
 |
| Figure 5 |
Figure 6 |
Figure 7 |
Figure 8 |
|
References
|
- J. G. Ziegler and N. B. Nichols, “Optimum settings for automatic controllers,”Trans. ASME, vol. 64, pp. 759–768, 1942.
- J. A. Ramos and P. Lopes dos Santos, “Mathematical Modeling, System Identification, and Controller Design of a Two TankSystem”Proceedings of the 46th IEEE Conference on Decision and Control New Orleans, LA, USA, Dec. 12-14, 2007.
- S.Nithya, N.Sivakumaran, T.Balasubramanian, and N.Anantharaman “Model based controller design for a spherical tank Process in realtime”IJSSST Vol. 9 No. 4, ISSN 1473-804x Online, 1473-8031,2008.
- C.E.Garcia and M.Morari, “Internal Model Control Design Procedure for Multivariable Systems”, Ind Eng. Chem. Process Des. Dev.,24, , pp.472-484,1985.
- M. Morari, E. Zafiriou, Robust Process Control, Prentice-Hall, Inc., Englewood Cliffs, N.J,1989.
- K. J. Åström and T. Hägglund, PID Controllers: Theory, Design, and Tuning. Research Triangle Park, NC: Instrument Soc. Amer., 1995.
- R. Gorez, “A survey of PID auto-tuning methods,” J. A, vol. 38, no. 1, pp. 3–10, 1997.
- O’Dwyer, Handbook of PI and PID Controller Tuning Rules. London, U.K.: Imperial College Press, 2003.
- ArputhaVijayaselvi, J.; Radhakrishnan, T.K.; Sundaram, S. “Model based IMC controller for process with dead time”. Instrum. Sci.Technol34, pp.463–474,2006.
- Labview Software.
- B.WayneBequtte, “Process control – Modeling, Design, and Simulation”, PHI,2006.
|