Research and Reviews - International Journals

International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Menu

ISSN ONLINE(2278-8875) PRINT (2320-3765)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

Model Reference Adaptive Control of Jacketed STIRRED-TANK Heater

Kalpesh B. Pathak1, Dipak M. Adhyaru2
  1. Assistant Professor, Dept. of Instrumentation & Control, Government Engg College, Gandhinagar, Gujarat, India
  2. Professor & Section Head, Dept. of Instrumentation & Control, Nirma University, Ahmedabad, Gujarat, India
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Abstract

Paper presents an important adaptive control technique, model reference adaptive control for temperature control in jacketed stirred tank heater. In heater a hot fluid is circulated through the jacket which is assumed to be perfectly mixed. Energy balance equations on the vessel and jacket fluids have been used as a model for simulation. Initially MIT rule technique has been applied for control. Data base of adjustment parameter θ and output of same has been saved for future strategy of neural network learning and training. By applying neural network based algorithm new values of θ have been generated. For uncertain system, results shows that as compared to conventional MRAC, Adjustment parameter θ generated using neural network leads to better result and robustness. Basics of MIT rule and small literature survey on stirred tank jacketed heater control and MRAC has also been discussed.

 

Keywords
CSTH, MRAC, Perturbation, MIT rule, Feedforward, Backpropagation

INTRODUCTION
Stirred-tank heater is an important instrument in chemical processes. Application of it covers pharmaceutical, pigment, resin, steel material, food, beverage industries and research laboratories. Simulation of an experimental continuous stirred tank heater (CSTH) pilot plant has been described in [1]. Volumetric equations, heat balance equations and algebraic equations derived from experimental data are presented. Equations are used for calibration of sensors and actuators and heat transfer through the heating coils. Many of these relationships have nonlinearities, and hard constraints such as the tank being full have been considered. Model uses measured noise and disturbances and not simulated values. It helps as a realistic platform for data-driven identification and fault detection. Modeling, design and simulation of important process control strategies and dynamics for bench-mark chemical systems have been discussed in [2]. Jacketed heater model discussed in same has been used here to apply and simulate model reference adaptive control (MRAC) strategy. As dynamics due to jacket adds one more order to the dynamics of tank, second order system has been discussed. Plant and model are of the same order as per need of MRAC. In [3] modeling, a controller formulation and simulation study of a CSTH has been discussed. Process control rig‟s analytical model is MIMO transfer function. Authors have considered the physical rig system parameters, boundary condition and limits. Trial and error method and heuristic approach has been used to design the PID controller to improve the system transient response for zero steady state error, as well as minimizing the rise time and overshoot.
Nonlinear model predictive control (NMPC) based on multiple neural networks has been considered in [4]. The control scheme includes a process model and an optimizer. Multiple neural networks are used to model the process and the model is then used in an NMPC scheme to control the process. Ensembles of artificial neural networks show improved generalization and noise-robustness capabilities in comparison to a single neural network. A genetic algorithm based optimizer is developed to determine a solution for the control trajectory. This optimizer is then combined with the sequential quadratic programming technique. Real-time control of a continuous stirred tank heater has been performed with this. Design and control architecture of a non-linear stirred tank heater based on its mathematical equivalent model has been presented in [5] involving both single and two manipulated of four input variables. Temperature of the fluid through the jacket and the flow rate of the fluid through the jacket and unmeasured disturbances have been considered. Model Predictive Controller and PID based controller results have been compared to maintain the tank temperature at 150°F, steady state value.
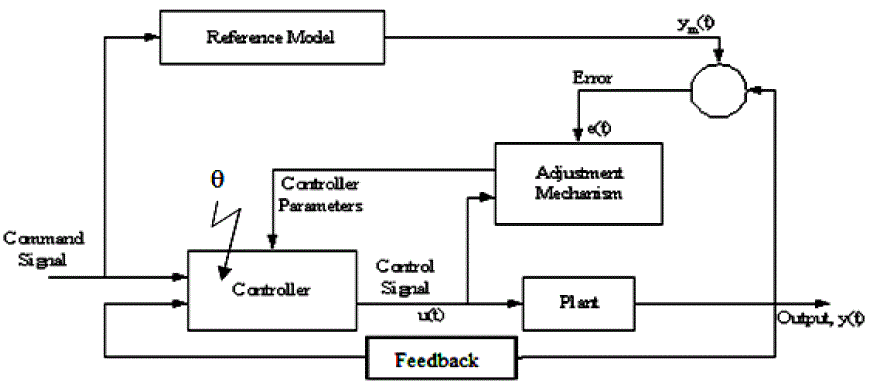
Basically a gradient scheme MIT rule is represented as 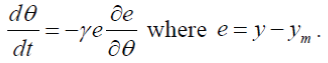image MRAC can be applied as MIT rule, modified MIT rule, Lyapunov stability method [9]. Soft computing can be added with all this approaches. Due to recent advances in computational facilities and soft computing, research publication with fuzzy logic and neural network (NN) has increased [6]. To proceed with same latest trend, in these paper results of applying MIT rule and with NN both have been discussed. In [6] recent survey of MRAC has been carried out based on control techniques and areas of application. Paper introduces that mostly, Model Reference Adaptive System (MRAS) consists of two loops, ordinary feedback loop as an inner loop and outer loop with controller parameter adjustment mechanism to minimize the difference between model output and process output.
With help of NN MRAC has been implemented in various effective ways. An approach to adaptive control, which uses the current or the online information as well as stored or background information for adaptation has been proposed in [7] for aerospace vehicles. Aerospace vehicles many times perform beyond their conventional flight envelopes and exhibit the robustness and adaptability to operate in uncertain environments. The current and conventional adaptive methodologies which use Neural Network based control methods use only the instantaneous states to tune the adaptive gains. It has been shown by results that using a combined online and background learning approach it is possible to overcome the rank one limitation on the adaptive law resulting in faster adaptation to the unknown dynamics. MRAC for arbitrary complex nonlinear discrete-time non-minimum phase system, time-delay system and minimum phase system has been proposed in [8]. An improved nearest neighbor clustering algorithm using an optimization strategy has been introduced as the on-line learning algorithm to regulate the parameters of the Radial basis function neural network to simplify the NN structure and accelerate the convergence speed. With the help of simulations it has been shown that control strategy based on direct Radial basis function neural network model reference adaptive control makes the multidimension nonlinear plants track multi-dimension reference signals quickly with satisfying robustness. A neural net based state feedback model reference adaptive control scheme is presented in [10] for a class of nonlinear plants. The presentation employs a time varying pseudo-linear state feedback control, where the state feedback gains being generated from the output of artificial neural networks. Both regulation and tracking control have been considered in simulation conducted on industrial robot and global stability of the scheme has been proved using Lyapunov theory. The extension of the scheme to MIMO plants is also included.
In [11] an observer design is proposed for nonlinear systems. The Hamilton–Jacobi–Bellman (HJB) equation based formulation has been developed. The HJB equation is formulated using a suitable non-quadratic term in the performance functional to tackle magnitude constraints on the observer gain. Observer is proved to be optimal with respect to meaningful cost. In the present algorithm With Lyapunov direct method, neural network is used to approximate value function to find approximate solution of HJB equation using least squares method. Presented algorithm has been applied on nonlinear systems with finite-time-horizon and infinite-time-horizon, simulation and theoretical results are presented for validation. An optimal control algorithm based on Hamilton–Jacobi–Bellman (HJB) equation, for the bounded robust controller design for finite-time-horizon nonlinear systems, is proposed in [12]. The bounded controller requires the knowledge of the upper bound of system uncertainty. In the proposed algorithm, neural network is used to approximate the time-varying solution of HJB equation using least squares method. Proposed algorithm has been applied on the nonlinear system with matched and unmatched system uncertainties.
Tracking control problem of the unmatched uncertain nonlinearly parameterized systems having unknown input nonlinearities has been presented in [13]. Two kinds of nonlinearities existing in the control inputs considered are nonsymmetric dead-zone input and continuous nonlinearly input. The controller has been proposed focusing zero closed loop tracking error. In either of two nonlinearity cases control technique effectively works by integrating adaptive backstepping technique and neural networks. A Hamilton-Jacobi-Bellman (HJB) equation based optimal control algorithm for robust controller design has been proposed for a nonlinear system in [14].The controller is shown to be optimal with respect to a cost functional with Lyapunov direct method. It includes penalty on the control effort, the maximum bound on system uncertainty and cross-coupling between system state and control. Neural network is used to approximate value function to find approximate solution of HJB equation using least squares method. Proposed algorithm has been applied on a nonlinear system with matched uncertainties and to the system having uncertainties in input matrix.

STIRRED-TANK HEATER WITH JACKET
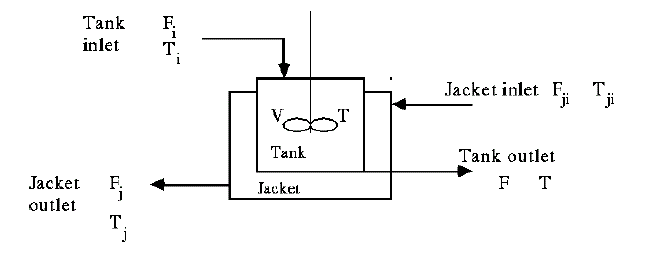
In a jacketed stirred-tank heater a hot fluid is circulated through the jacket which is assumed to be perfectly mixed. Heat flow between the jacket and vessel increases the energy content of the vessel fluid. The rate of heat transfer from the jacket fluid to the vessel fluid is
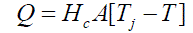image (1)
Where H C is the overall heat transfer coefficient and A is the area for heat transfer. Volume and density are assumed to be constant, Feed rate Fi=F.
Generally simplest Modeling technique involves Mass and Energy balance principle. Energy balances on the vessel and jacket fluids result in the following equations.
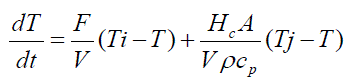image (2)
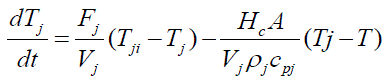image (3)
Here the outputs are the vessel and jacket temperatures, which are also the states; the inputs are the jacket flow rate, feed flow rate, feed temperature, and jacket inlet temperature. If the outputs, states, and inputs are in deviation variable form means they are perturbations from steady value. Vessel and jacket temperatures need to be maintained at desired set point.
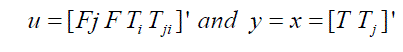image (4)
Feedforward backpropagation network has been created using „newff‟ command in MATLAB® script. The first layer has weights coming from the input. Each subsequent layer has a weight coming from the previous layer. All layers have biases. The last layer becomes network output. With network training functions weight and bias states have been updated according to Levenberg-Marquardt optimization. Training occurs until a maximum number of epochs occur, the performance goal is met, or any other stopping condition occurs. „trainlm‟ is the default training function because it is very fast, but it requires a lot of memory to run. It represents Levenberg-Marquardt backpropagation. Unlike conventional control, where plant output needs to meet reference input trajectory, here plant output need model output trajectory. So target for supervised learning is decided accordingly.

RESULTS & DISCUSSION
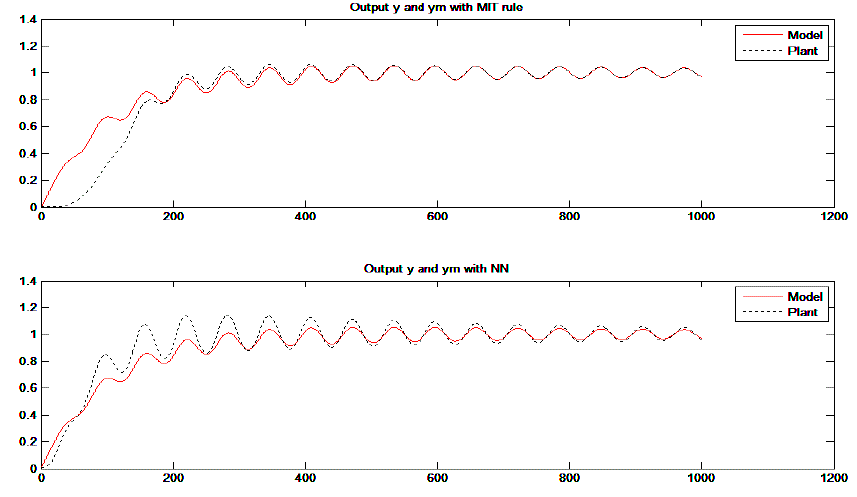
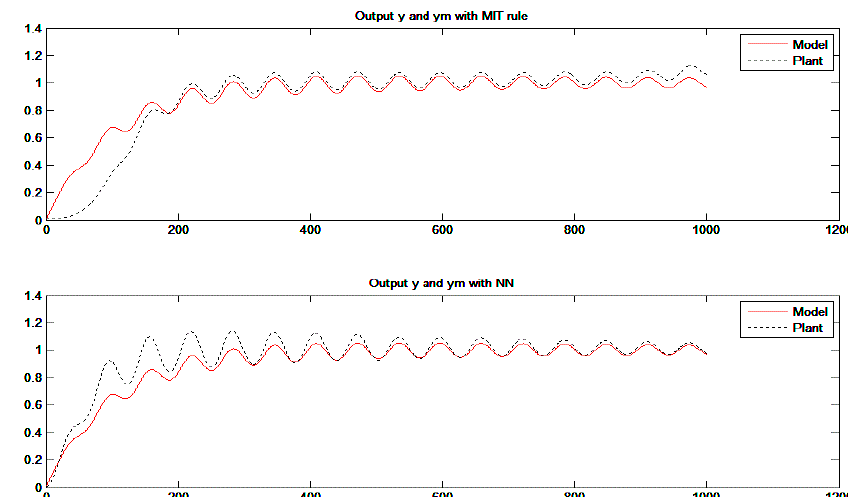
Initially MRAC has been applied for the jacketed stirred-tank heater system considering all parameters without uncertainty. The results are as shown in Fig 3 below. Values of parameters for simulation are F=0.01; V=1; Fj=0.1; Vj=1; HC=.1; A=1; V=1; r=1; cp=1; vj=1; rj=1;cpj=1; Ti=1; Tjin=1 and adaptation gain gma=0.9. All the considered values are in deviation variable form. Observation shows second order unit step response in both cases.
Observation of both results reveals that in each case plant output tracks model output in much closer neighbourhood. In case of using mathematical formula of MIT rule, as shown in upper part of Fig. 3 after initial 200 sampling instants plant output exactly tracks the model output throughout the simulation time. If θ generated using NN from the database of θ from initial part of simulation, we get simulation result as shown in lower part of Fig. 3.
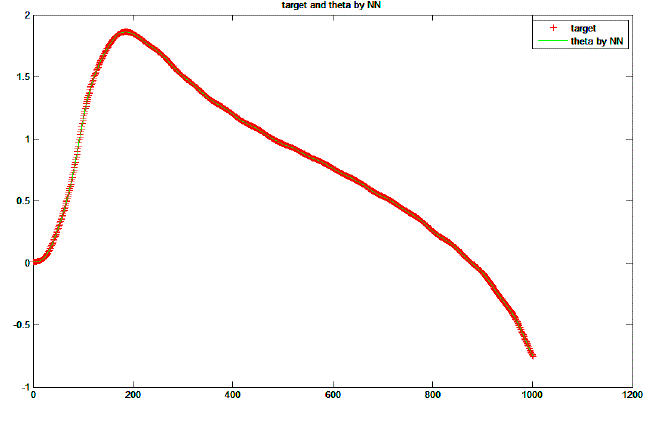
Fig. 4 shows that new θ generated from target θ, exactly matches the same. It shows perfection in supervised learning using available data of adjustment parameter. This selection of proper learning, training and adaptation technique helps us while controlling systems with uncertain parameters because in such cases adaptation is compulsory.
In later part of simulation, some uncertainty was added in ordinary differential equations of the plant and result with supplication of MIT rule and NN has been compared. Up to some extent, much difference could not be observed. If uncertainty added is still more, performance using adjustment parameter generated using NN give better result as shown in Fig. 5. Observation reveals that NN technique takes time for adaptation so after approx. 500 instants onward NN output is much improved compared to MIT rule shown in upper part of Fig. 5. Later on simulation result shows that plant output perfectly tracks the model output.

CONCLUSION
Soft computing technique NN and MIT rule technique have been used for simulation. Sufficient information has been gathered and necessary model of stirred tank jacketed heater has been picked with survey of papers and books related to Stirred tank jacketed heater and NN based MRAC. Comparisons of Implementation of MRAC using MIT rule and NN in two separate cases have been discussed in paper. Some assumptions about parameter values and perturbation values have been done. Energy balance equations on the vessel and jacket fluids have been used as a model for simulation. Observation of results in both cases reveals that selection of proper value of adaptation gain and proper learning and training algorithm in NN leads to desirable results. Negative gradient of θ satisfies condition of convergence for stability. Plant output tracks model output in much closer neighbourhood for each case. Addition of uncertainy in the plant dynamics leads to some more deduction. Simulation results after adding more uncertainty in plant reveals that with NN based MRAC control system robustness increases.

Figures at a glance
Figure Figure Figure Figure Figure
Figure 1 Figure 2 Figure 3 Figure 4 Figure 5

References