Keywords
|
| Non-linear process, WMPI, IMC, Chidambaram tuning rule. |
INTRODUCTION
|
| Conical tank control of industrial process is a challenging task for numerous bases due to its nonlinearity. The control of liquid level in conical tank is a major trouble in industrial process. A level is far above the surface may possibly disturb process reaction equilibria make happen spoil to equipment. If the height is near to the surface it may perhaps bad result for the series operation. So liquid level control in process industries is significant and general task. Conventional controllers are broadly used in industries since they are trouble free, robust, and well known to the field operator. Practical system are not precisely linear but mat be represented as linearized models around a nominal Operating point, the controller parameters tuned at that point may not reflect the real time system characteristics due to variations in process parameters. For controlling the liquid level in conical tank we make use of Wiener model PI controller. Here the tuning rules based on Chidambaram method is designed initially and the results are compared with internal model controller (IMC).In this task the process model is carry out trial and determined by using system identification method. The method adopted here for system identification is step test and is done in real time with Labview using NI DAQ. |
PROCESS BLOCK DIAGRAM
|
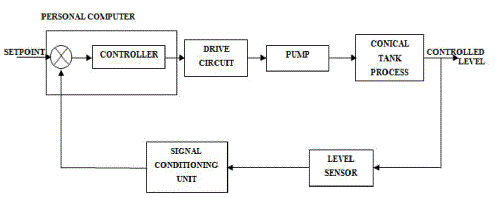
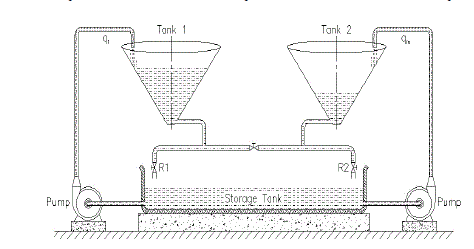
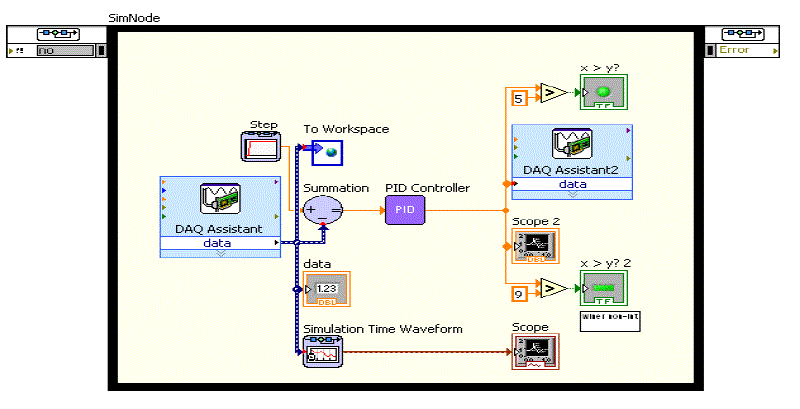
| A real time experimental setup for extremely non-linear conical tank is constructed. The process control system is interfaced with labview using PCI 6221 DAQ module to the personal computer. The block diagram for this system is shown in Figure 1, it consists of a labview based controller, driver circuit used to operate the solenoid valve, nonlinear conical tank, capacitance based level sensor, signal conditioning unit. |
EXPRIMENTAL SETUP
|
| The control parameter prefers here is the level. Capacitance based level transmitter arrangement senses the level from the process and converts into electrical signal. Then the corresponding electrical signal is fed to the current to voltage converter which in turn produces proportional voltage signal to the computer. |
| The experimental setup shows the closed loop system which maintains water level in a conical tank and also perform the non-interacting & interacting. The actual tank water level sensed by the level transmitter is feedback to the level controller & compared with a desired level to produce the required control action that will position the level control as needed to maintain desired level. Now the controller decides the control action & it is given to the voltage to current converter. The FCE is now controlled by the resulting pneumatic signal. This in turn control the inflow to the conical tank & the level is also controlled in both non-interacting & interacting system. |
| The Tank Specifications are as follows: |
| Height : 40 cm |
| Volume : 11.39 litres |
| Bottom diameter : 10 cm |
| Top diameter : 25 cm |
| Angle : 10 deg |
| Material : Stainless Steel |
MATHEMATICAL MODELING
|
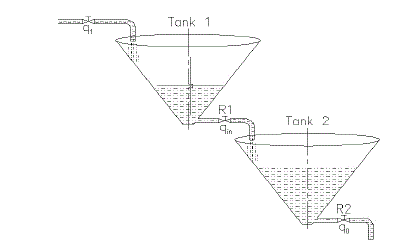
| A. Mathematical Modeling of Two Conical Tanks of Non-Interacting System |
| System is said to be non-interacting the dynamic behaviour of the first system will affect the dynamic behaviour of the second system while the dynamic behaviour of the second system does not affect the first system. Let us define, |
| H1=height of the conical tank 1 cm |
| H2=height of the conical tank 2 cm |
| V = total volume of the conical tank |
| qin(s)=volumetric flow rate of the inlet stream (lph) |
| q1(s)volumetric flow rate of the outlet stream (lph) |
| R1=Restriction element |
| H=Maximum height of the conical tank |
| According to law of conservation of mass, |
| Accumulation of mass within a system = Flow of mass into the system - Flow of mass out to the system |
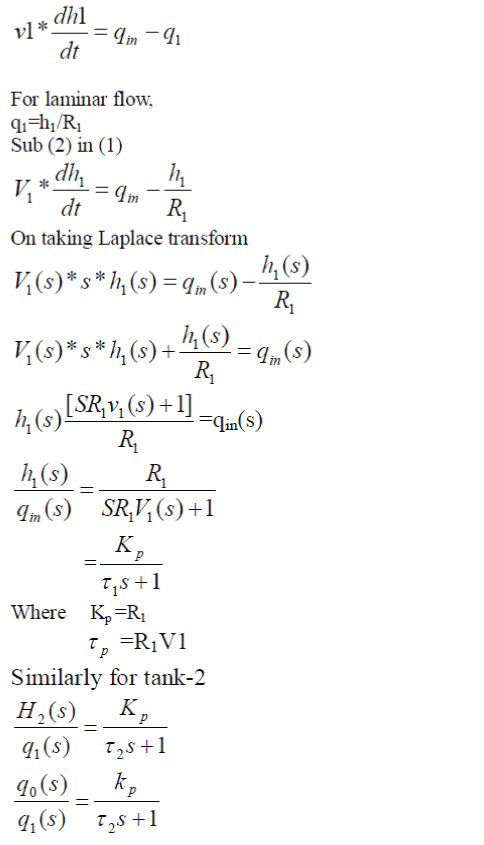 |
 |
| B. Mathematical Modeling of Two Conical Tanks of Interacting System |
| System is said to be interacting then the dynamic behaviour of the first system will affects the dynamic behaviour of the second system while the dynamics of second system will affects the dynamics of first system. |
 |
TECHNIQUE FOR CONTROLLER DESIGN
|
| A.COHEN COON METHOD |
| For a non-linear system the output to be settled region by region for finding that we divide our measurements in three sections like 0 to 12cm , 12 to 24cm , and 24 to 36cm. |
| We obtain the transfer function from the experimental data. |
| From this transfer function obtain kc, ti, td by using cohen coon method and simulated this value using matlab for the output response. |
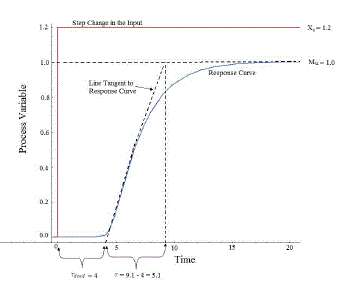
| With respect to the order of the system the shape of the system will varies. Whatever may be the order we are approximating first order with dead zone. |
| 1. Bring the system or a process to a steady state value. |
| 2. Give a small step change to the input. Sketch the response. |
| 3. The point at which the response starts increase vertically is known as point of inflection. |
| 4. Draw a tangent on the point of inflection. |
| 5. The point at which the tangent meets the time X-axis is dead time. |
| 6. Draw a slope on the tangent and let it be slope. |
| B.ZIEGLER- NICHOLS Method |
| Ziegler Nichols is a method of controller setting assignment that has come to be associated with their name. This technique, also called the ultimate cycle method, is based on adjusting a closed loop until steady oscillations occur. Controller settings are then based on the conditions that generate the cycling. The PI parameters are calculated as: Kc=0.9τ/kpτd ; τi=3.33τ. The general drawback is that the resulting closed loop system is often more oscillatory than desirable. |
| C. Internal Model Controller |
| The controller is designed to provide nominal performance, and a non-linear filter is added to make the controller implementable and to account for plant/model mismatch. An important advantage of the new approach is that the assumption of full- state feedback inherent in most input-output linearization schemes is eliminated. However, the proposed IMC strategy is restricted to open-loop stable systems with stable inverses. Under mild assumptions, the closed-loop system possesses the samestability, perfect control, and zero offset properties as linear IMC The PI parameters are calculated as: |
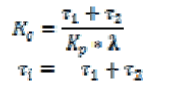 |
PADMASREE-SRINIVAS-CHIDAMBARAM TECHNIQUE (PSCT)
|
| The performance specification for stable system cannot be met for the unstable system, Chidambaram have used tuning parameter. The performance of the controller designed by the method significantly better than that of pole placement method. Later Chidambaram and padmasree have extended the method to integrating system with dead time, and the performance of the controller designed is significantly better than that of the optimization method. The PI parameters are calculated as: kc*kp=(τ/τd)+0.5; |
| πi=π+0.5πd. |
| The Table - 4 represent the calculation of error for both Non-Interacting & Interacting systems by using IMC & CHIDAMBARAM techniques. By comparing these two techniques the error was minimized in Chidambaram technique. So that wiener model PI controller was designed using Chidambaram technique. |
WIENER MODEL BASED PI CONTROLLER
|
| The aim of this study was the development and real time implementation of a wiener mode l based PI controller (WMPIC) for a conical tank level process. The conical tank level process exhibits severe static non-linear behaviour and dynamic characteristics. Here, a WMPIC structure was developed by the way compensating the process static nonlinearity. Tuning rules suggested by padmasree-srinivas-chidambaram and internal model controller were considered here for designing the controller. The real time implementation results of wiener model based PI controller were designed. The performance this controller was analyzed in terms of Integral Square Error(ISE), Integral Absolute Error(IAE),Integral Time Absolute Error(ITAE). |
| A. PROCEDURE FOR DESIGNING WMPIC: |
| • From the tentative information, worst case of model parameters is selected. Larger process gain, larger delay and smaller time constant of the process. |
| • PI controller settings have been evaluated based on the above selected model parameter using PSCTR (padmasree-srinivas-chidambaram tuning rules) and IMC (internal model controller). |
| • Using the values obtained in step no :( 1 & 2) developed a wiener model based PI controller. |
SIMULATION RESULTS
|
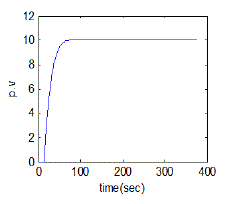
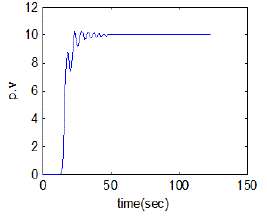
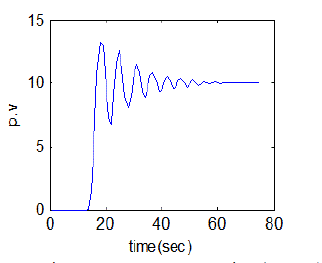
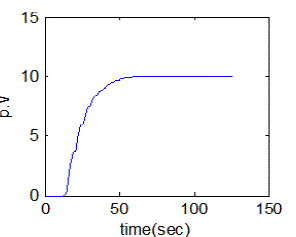
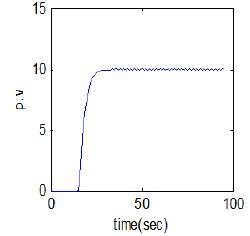
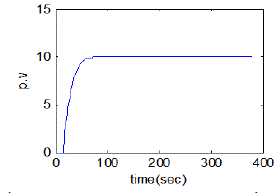
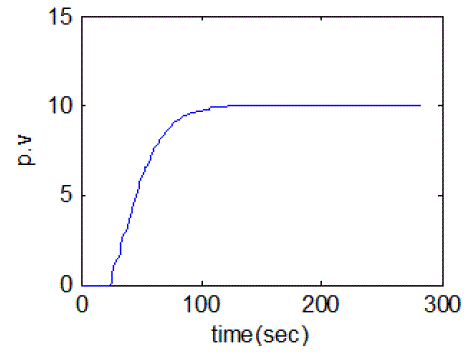
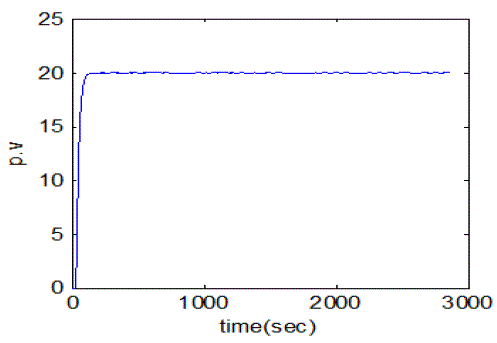
| The simulation and real time responses for wiener model PI control scheme for non-interacting non-linear system and interacting non-linear system were experienced at different operating points. The simulation was passed out using matlab and the real time control of both interacting & non-interacting was done with lab view. Fig. 18 and Fig. 19 show the simulated response of conical tank interacting system and conical tank non-interacting system was done with various level set point and Fig.20 and Fig.21 show the real-time control of both interacting & non-interacting with wiener model PI controller. |
CONCLUSION AND FUTURE WORK
|
| The wiener model PI controller is designed and applied to both non-interacting & interacting system for level control. The wiener model PI controller parameters are tuned for several height of tank and then it is simulated under parameter changes. Control of liquid level in the both non-interacting & interacting system process is a difficult task because of its non-linear behaviour. By proper wiener model PI controller tuning, level control all the categories is first carried out in matlab and then analyzed in real time using labview. The future work can be extended for controlling of both noninteracting & interacting using artificial intelligence. |
Tables at a glance
|
 |
 |
 |
 |
 |
| Table 1 |
Table 2 |
Table 3 |
Table 4 |
Table 5 |
|
Figures at a glance
|
 |
 |
 |
 |
 |
| Figure 1 |
Figure 2 |
Figure 3 |
Figure 4 |
Figure 5 |
 |
 |
 |
 |
 |
| Figure 6 |
Figure 7 |
Figure 8 |
Figure 9 |
Figure 10 |
 |
 |
 |
 |
 |
| Figure 11 |
Figure 12 |
Figure 13 |
Figure 14 |
Figure 15 |
|
References
|
- P.K.BHABA, S.SATHISH BABU, A, ASOKAN & T.KARUNANITHI, “REAL IMPLEMENTATION OF WIENER MODEL PI (WMPI)CONTROLLER IN A CONICAL TANK LIQUID LEVEL PROCESS,” 2007.
- PADMASREE.R. M.N.SRINIVAS & M.CHIDAMBARAM,” A SIMPLE METHOD OF TUNING PID CONTROLLERS FOR STABLE ANDUNSTABLE FOPTD SYSTEMS,”2004
- K.HARIKRISHNA, J.SATHEESH KUMAR, MAHABOOB SHAIK,”REAL TIME IMPLEMENTATION OF MODEL BASEDCONTROLLER FOR A SPHERICAL TANK”VOLUME.2, MAY 2013.
- ANNA JOSEPH, J.SAMSON ISAAC,”REAL TIOME IMPLEMENTATION OF MODEL REFERNCE ADAPTIVE CONTROLLER FOR ACONICAL TANK”VOLUME.2, 2013.
- K.BARRILJAWATHA,”ADAPTIVE CONTROL TECHNIQUE FOR TWO TANKS CONICAL INTERACTIVE SYSTEM”,INTERNATIONAL CONFERENCE ON COMPUTING AND CONTROL ENGINEERING, APRIL 2013.
- N.S.BHUVANESWARI, G.UMA&T.R.RANGASWAMY.NEURO BASED “MODEL REFERENCE ADAPTIVE CONTROL OF A CONICALTANK LEVEL PROCESS”, CONTROL AND INTELLIGENCE STYLE, VOLUME .36, 2008.
|