Keywords
|
| Single phase induction motor,bifurcation, chaos,non-linear,periodicity. |
INTRODUCTION
|
| Single-phase induction machines have a major industrial significance, being well suited for applications where cost is the dominant consideration, and performance requirements are modest.The split phase induction motor has two windings, the main winding and the auxiliary winding. These windings are displaced in space by 90 electrical. The auxiliary winding has higher current ratio between resistance and reactance, by designing it at a higher current density. In modeling performance characteristics of the induction motors, in question, circuit models of lumped parameters are still often used due to their simplicity and fast computation. At first approximation of the mathematical models linearity of magnetic circuit is assumed. |
| Chaos is aperiodic long term behavior in a deterministic system that exhibits sensitive dependence on initial conditions. Thistheory is a field of study in mathematics, with applications in several disciplines including physics, engineering, economics, biology, and philosophy.As the initial state of a practical system can only be specified with some tolerance, the long-term behaviour of a chaotic system can never be predicted accurately. |
D-Q AXIS MODELLINGOF THE MOTOR
|
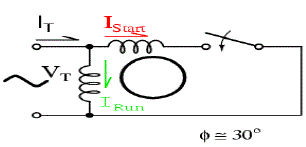
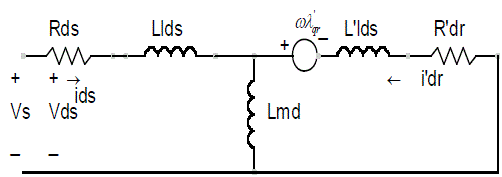
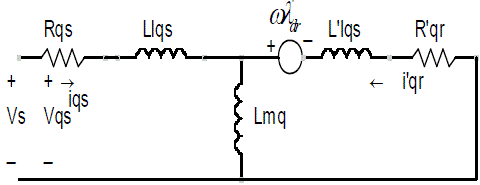
| The D-Q model a single phase induction machine can be considered to be an unsymmetrical two phase induction machine. To build a Motor model, we need mainly The Stator and Rotor Voltage equations.Let us take the following motor Here we see that their exist some complexity of the voltage equations due to the time varying mutual inductances between stator and rotor circuits(circuits in relative motion).To eliminate the time varying variables we need a transformation tool. The general Transformation refers the motor variables to a reference frame that rotates at an arbitrary angular velocity. |
| Commonly Used Reference Frame : |
 |
| The voltage equation can be written as |
 |
| Where K= D axis to Q axis turns ratio and K=1 also. |
| Here we used Stationary Reference frame. |
 |
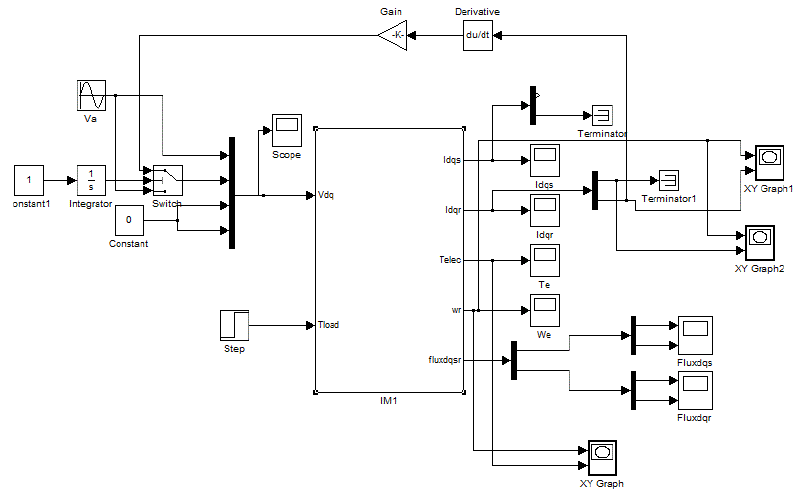
MATLAB/SIMULINK MODELLING
|
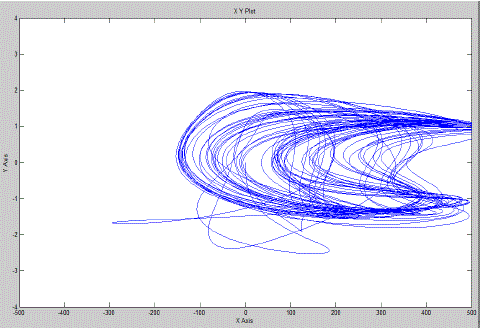
| The Two (main and auxiliary) stator windings are displaced 90 degree in space.The modelling of the single phase induction motor projects the non-linear model of the system.The variation of system settling points with the variation of system parameters is defined as bifurcation of the system. Here we vary the operating voltage keeping other variables constant. It can be observed that the chaotic speed waveforms gives the well-known chaotic properties, namely random-like but bounded oscillations. Physically, these chaotic motions reveal the unbalanced status of the interaction between the magnetic fields by the main winding and the auxiliary winding.Also, these waveforms are a-periodic and very sensitive to the initial condition. |
MOTOR PARAMETERS
|
 |
RESULTS
|
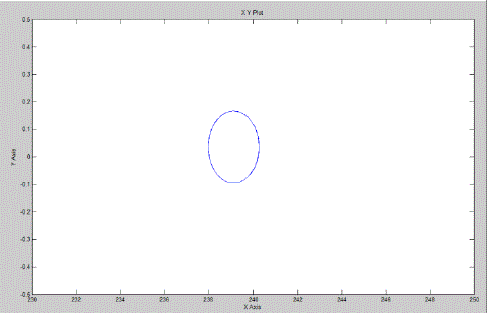
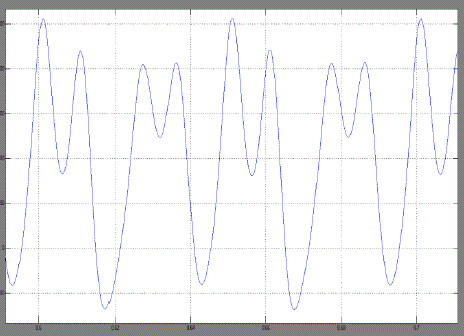
| Case 1:When voltage = 160V periodicity has been observed in speed waveform. i.e. period 1 has been achieved . |
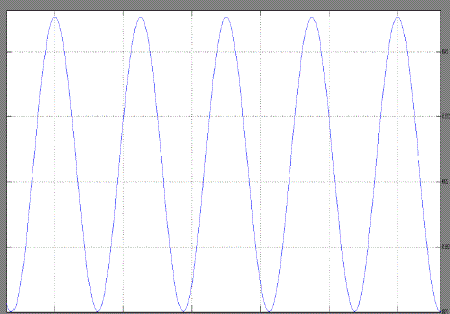
| Case 2:- As the motor operating voltage changes to 180 volt the phenomenon changes and the speed waveform periodicity has been changed from one to two(period 5). |
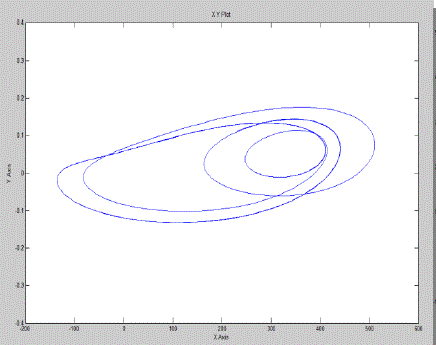
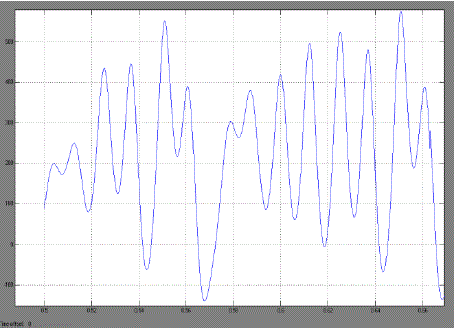
| Case 3 :Periodicity becomes too large to determine and the system become chaotic.Here voltage = 220 V |
CONCLUSION
|
| The non-linear phenomenon in split-phase induction motors are observed as the voltage(V) is varied.This paper firstly proposed a novel chaotic-speed split phase type SPIM drive for application to cooling fans. Figures have shown above represents the speed waveforms and the corresponding phase-portraits, at various periodic-speed operations, i.e. the period- 1, period-5 and chaotic operations. As the voltage increases the angular speed becomes chaotic. We found lots of application of chaotic speed of induction motor such as cooling system, mixture grander, air compressor etc.These waveforms are consistent with the well-known phenomenon of inevitable torque pulsation. It should be noted that once the operating condition are known, the motor parameter whose variation bringing chaos may be more than one possible.The proposed chaotic motion can be adopted to improve heat transfer and hence the cooling effect for homogeneity. |
Figures at a glance
|
 |
 |
 |
 |
| Figure 1a |
Figure 2 |
Figure 3 |
Figure 4 |
 |
 |
 |
 |
| Figure 5 |
Figure 6 |
Figure 7 |
Figure 8 |
 |
 |
 |
| Figure 9 |
Figure 10 |
Figure 11 |
|
| |
References
|
- J.H. Chen, K.T. Chau and C.C. Chan, “Analysis of chaos in current mode controlled dc drive systems,” IEEE Transactions on Industrial Electronics, vol. 47, pp. 67-76, 2000.
- Dynamic simulation of electric machinery using MATLAB/SIMULINK by Chee-Mun Ong. Prentice Hall PTR 1998, ISBN 0-13-723785-5
- K.T. Chau and J.H. Chen, “Modeling, analysis and experimentation of chaos in a switched reluctance drive system,” IEEE Transactions on Circuits and Systems - I, vol. 50, pp. 712-716, 2003.
- Y. Gao and K.T. Chau, “Design of permanent magnets to avoid chaos in PM synchronous machines,” IEEE Transactions on Magnetics, vol. 39, no. 5,pp. 2995-2998, 2003.
- Gao, Y; Chau, KT; Ye, S “A novel chaotic-speed single-phase induction motor drive for cooling fans”, The 40th I A S Annual Meeting Industry Applications Conference Record, Hong Kong, China, 2-6 October 2005, v. 2, pp. 1337-1341.
|