MODELLING AND REAL TIME CONTROL OF TWO CONICAL TANK SYSTEMS OF NON-INTERACTING AND INTERACTING TYPE

Abstract

Nonlinear process control is a difficult task in process industries. Real processes often exhibit nonlinear behaviour. Many process industries use conical tanks because of its shape contributes to better drainage. Conical tanks are used widely in leaching extractions in pharmaceutical and chemical industries, as well as in food processing industry. It is a kind of multiple-use equipment, designed for boiling and extraction working procedure. So control of conical tank presents a challenging problem due to its non-linearity and constantly changing cross section. In this project work of the mathematical modelling of Single Conical Tank, Two Conical Tanks of Non-Interacting type System and Two Conical Tanks of Interacting type System is designed and the responses of the processes are obtained. To control level in all the above categories, tuning of controller parameters are determined by Ziegler-Nichols (Z-N) tuning method. After proper tuning by Z-N method, conventional PID controller is applied to the above three categories and their responses are analysed both by MATLAB simulation and by real-time.

Keywords

Nonlinear system, PID Controller, Two Conical Tanks of Interacting System, Non-Interacting System.

INTRODUCTION

The control of liquid level in tanks and flow of the tank is a basic problem in process industries. A level that is too high may upset reaction equilibria, cause damage to equipment, or result in spillage of valuable or hazardous material. If the level is too low, it may have bad consequences for the sequential operations. Hence, control of liquid level is an important and common task in process industries. Chemical processes present many challenging control problems due to their nonlinear dynamic behaviour. Nonlinear models are used where accuracy over a wider range of operation is required where they can be directly incorporated into control algorithms. Because of the inherent nonlinearity most of the chemical process industries are in need of traditional control techniques. The nonlinear system taken up for the study is the conical tank which finds wide application in process industries. It gives nonlinearity because of its change in shape. Their shape contributes to better dispersal on solids, when mixing and provide more complete drainage especially for viscous liquids, slurries and solid mixtures. Designing of controller for a nonlinear process is an important problem.

The main aim is to maintain the process at its operating range and design the controller to achieve its optimum performance. This project deals with two conical tanks of non-interacting type and two conical tanks of interacting type. In two conical tanks of non-interacting type the two tanks are arranged in series so that the outflow from the first tank is the inlet flow to the second tank. The variation in the level of the second tank does not affect the level of the first tank. This type of system is referred as a non-interacting system. In case of two conical tanks of interacting type, the two tanks are arranged in parallel and two identical pumps are used to deliver two liquid inlet flows to two tanks through the two control valves. These two tanks are interconnected at the bottom of the tank through the valve and variation in the level of the second tank affects the level of the first tank. First conventional PID control technique is applied for a single conical system and also applied for two conical tanks of non-interacting type and two conical tanks of interacting type. The responses of the above categories are carried out by using MATLAB based simulation and also real time control is verified.

MATHEMATICAL MODELING

A. Mathematical Modelling of Two Conical Tanks of Non-Interacting Type System(TCTNIS)

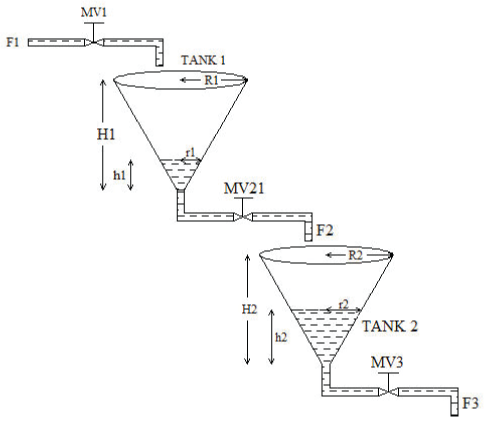
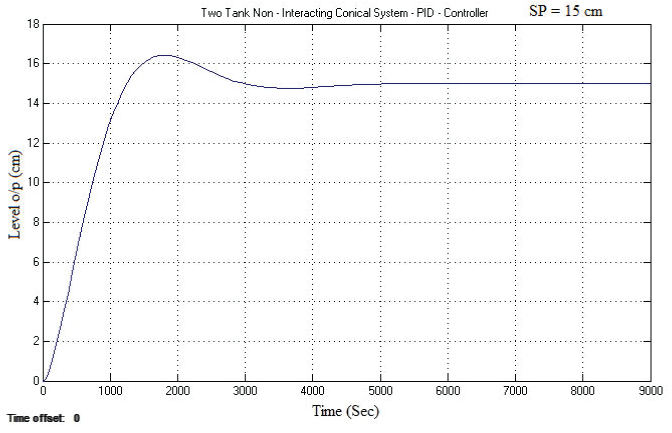
Two tanks are arranged in series so that the outflow from the first tank is the inlet flow to the second tank. Here the outflow from the first tank depends only on the height of the first tank and the variation in the height of the second tank does not affect the response of first tank. This type of system is said to be non interacting system. The Fig. 1 represents the two conical tanks of interacting type system.

By considering the following design parameters, the transfer function of the proposed system is expressed as follows: Considering tank dimensions has,

Total Height of the tank H = 60 cm

Top Radius of the Tank R = 15 cm

Valve Co-efficient Cv = 5

Transportation delay =0.3sec

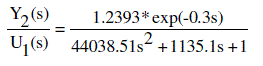B. Mathematical Modelling of Two Conical Tanks of Interacting Type System(TCTIS)

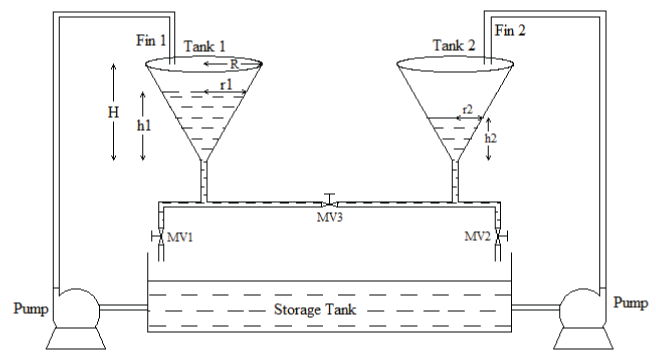
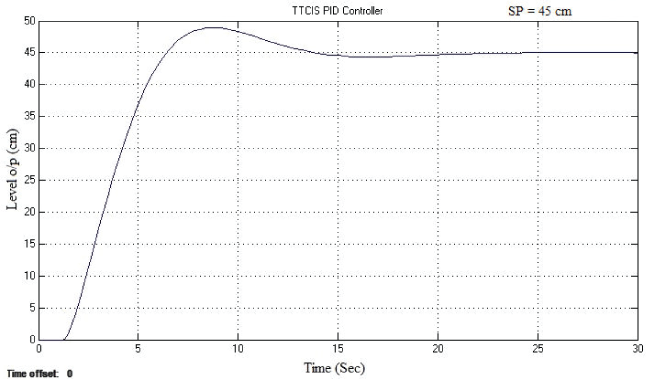
The schematic diagram of two conical tanks of interacting type system is shown in Fig.2. It is a two tank benchmark problem that has been used by a number of researchers. TCTIS consists of two identical conical tanks, two identical pumps that deliver the liquid flows in Fin1 and Fin2 to tank 1 and tank 2 through the two control valves MV1 and MV2. In tank, the liquid should be of constant density, the tank to have uniform cross sectional area but the outflow in the tank is not linear due to the variation in the depth of the conical tank. Our objective is to find a transfer function that relates to 2 Y (Nominal Height of Tank 2) to 1 U (Inlet Flow of Tank 1) that is y2(s)/u1(s) The approach will be to obtain a transfer function for each tank, y1(s)/u1(s) and y2(s)/u2(s)

For Steady State Condition h1 = 45 cm and 2 h = 20 cm, β1 = 5 and β2 = 2

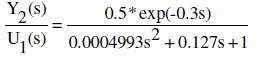SIMULATION RESULTS

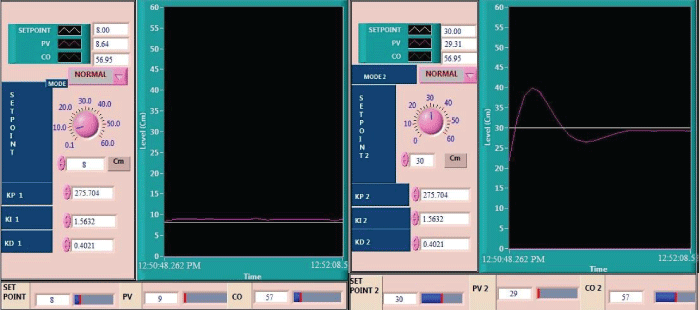
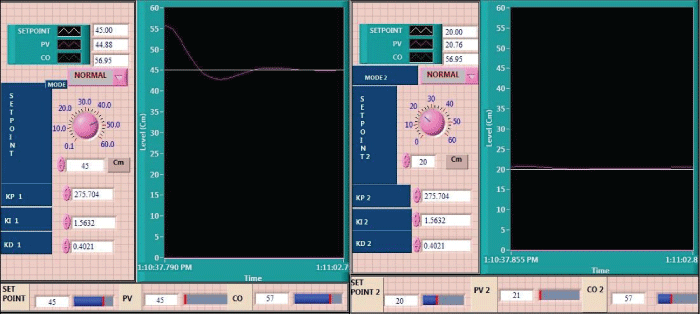
The simulation and real time responses for conventional PID control scheme for non-interacting non linear system and interacting non linear systems were tested at various operating points by considering TCTNIS and TCTIS. The simulation was carried out using MATLAB and the real time control of TCTNIS and TCTIS was done with LabVIEW. Fig. 3 and Fig. 4 show the simulated response of TCTNIS and TCTIS with various level set points and Fig. 5 and Fig. 6 show the real-time control of TCTNIS and TCTIS with PID controller.

CONCLUSION

The conventional PID controller is designed and applied to two conical tanks of non interacting type system and two conical tanks of interacting type system for level control. The conventional PID controller parameters are tuned for various heights of tank and then it is simulated under Parameter changes. Control of level in the two conical tanks of non interacting type system and two conical tanks of interacting type system processes were difficult because of their non-linear behaviour. By proper PID controller tuning, level control in all the three categories is first carried out in MATLAB and then analyzed in real time. The future work can be extended for controlling of TCTNIS and TCTIS using Adaptive controller for better performances.

Figures at a glance

Figure 1 Figure 2 Figure 3 Figure 4 Figure 5 Figure 6

References

Bhuvaneswari.N.S, Uma.G and Rangaswamy.T.R,‘Adaptive and optimal control of a non-linear process using intelligent controllers’, Elsevier,Applied Soft Computing vol. 9, pp. 182–190, 2009. BarrilJawatha.K, ‘Adaptive Control Technique for Two Tanks Conical Interacting System’, International Conference on Computing andControl Engineering, 2012. Ravi.V.R and Thyagarajan.T, ‘Application of Adaptive Control Technique to Interacting Non Linear Systems’, International Conference onElectronics Computer Technology, vol:2, pp. 386 – 392, 2011. Sukanya R, Warier and SivanandamVenkatesh, ‘Design of Controllers based on MPC for a Conical Tank System’, IEEE-InternationalConference on Advances In Engineering, Science And Management, 2012. Marshiana.D and Thirusakthimurugan.P, ‘Design of Ziegler Nichols Tuning controller for a Non-linear System’ International Conference onComputing and Control Engineering, 2012.