Modelling of Dynamic Response of WO3 Gas Sensors under CO

Abstract

We propose a model for gas sensors dynamic response which puts emphasis on conduction properties of n-type semiconductors. This model gives a physico-chemical description of gas detection mechanisms, by focusing on the extrinsic behavior of the sensor in the presence of reducing gas. Theoretical modeling of the sensor resistance in respect to experimental results was done to optimize sensor performances and also to better understand the gas detection mechanisms. This model especially applies in the case of exposure to low gas concentrations.

Keywords

Gas sensors, WO₃, Resistance modelling, CO gas sensors.

Introduction

Due to their remarkable gas detection properties, metal-oxide semiconductors have been long known as promising materials mainly intended for the detection of a wide range of reducing and oxidizing gases [1-4]. These materials are either n-type semiconductors (e.g. SnO₂, WO₃, TiO₂ and ZnO) or p-type semiconductors (e.g. CuO and Co₃O₄). We focus here on the n-type gas sensing metal-oxide materials; especially on tungsten trioxide (WO₃) which is part of good candidates for gas sensing applications due to its impressive properties [5-8]. The n-type semiconductor (WO₃) have a native non-stoichiometric structures and free electrons originating from oxygen vacancies which contribute to electronic conductivity change when the sensors are exposed to gases. As a consequence, depletion layers appear in the vicinity of the surface and around grain boundaries giving rise to potential barriers. In the presence of reducing gas, the sensor resistance will decrease as a consequence of reactions between gas molecules and the already ionized oxygen on the surface which manifested by a re-injection of electrons to the materials when pre-adsorbed oxygen leaves the surface with the reducing species.

In the present work, we report theoretical approach which takes into account the physics of semiconductors interfaces as well as the chemistry of gas adsorption and put emphasis on some properties of the sensitive layer which provides some knowledge of the sensor behavior. The modeling of semiconductor gas sensors aims at quantitative evaluation of the sensor response to different gases as a function of the sensor properties and operating conditions. It is performed on experimental resistance transients under carbon monoxide for different concentrations to show the applicability and the accuracy of the model.

We perform the calculation for a single grain boundary; mainly the properties of single grain-boundaries are considered. Then the whole granular material is modeled based on density on grain boundary and the dimensions of the sensitive layer, which allows the total resistance to be calculated in a simple manner. This approach of the material structure is a first approximation, which consists of a set of identical grain boundaries, is based on numerous studies which shown that it’s enough to explain our experimental results and can be applied for the most metal oxides [9,10].

Theoretical Background

Current density across the grain boundary

Taking into account the granular aspect of the metal oxide gas sensors, the WO3 layer may be considered as a succession of n-type bi-crystals, thus the grain boundary represents the interface between crystals. This specific area shows significant electric activity and can affect considerably the transport properties of the material when gas adsorption is done. The adsorption process gives rise to a depletion layers around grains due to a charge trapping phenomenon, resulting in a potential barrier. In the case of unbiased grain boundary (Figure 1a), the depletion widths on both sides of the boundary are equals. The potential barrier V_b⁰ at the grain boundary can be solved using Poisson equation and the neutrality equation 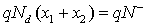[10,1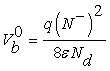1]

(1)

Where the superscript 0 indicates that the values refer to the case of unbiased grain boundary.

N^–, N_d and ε indicate the density (per unit area) of the charge at the grain boundary, the density of donors which are supposed all ionized at the working temperature [10] and permittivity of sensing material, respectively. It should be noticed that the Schottky approximation is applied in this case, i.e., all the electrons are depleted from the depletion layer and captured by surface states.

When a bias voltaje V_ab is applied in the grain boundary, the double Schottky barrier becomes asymmetric (Figure 1b). Thus, the barriers on either side of the grain boundary must obey the condition V₂ = V₁ - V_ab. In this case, the depletion widths are not equals while the total width of the depletion region still invariant according to neutrality equation.

The current density in one dimension across the grain boundary can be determined using the drift-diffusion theory [10,1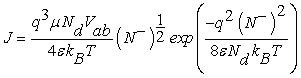2]

(2)

Which is proportional to the applied voltage and directly related to the amount of charge trapping given by N^– caused by gas adsorption. Thus, the current density of the sensitive layer will be determined if N^– is known.

Gas sensing mechanism

The main gas sensing process in metal oxide gas sensors is oxygen adsorption from air, usually in the ionized form at high temperatures after a fast step weak adsorption in the neutral form. This corresponds to a charge transfer between the WO₃ sensitive layer and the adsorbed oxygen which gives rise to a charge trapping phenomenon.

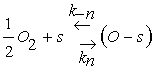(3)

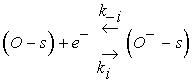(4)

Eq. 3 describes the adsorption of oxygen species in the neutral form at a site s which involves two reaction constants denoted by K_n and K_−n for the direct and inverse reactions. However, Eq. 4 is devoted to the ionization process after neutral adsorption and the associated constants are K_−i and K_i for the direct and inverse oxygen ionization reactions. The adsorption in the neutral form is a fast process which allows us to assume that the density of oxygen atoms adsorbed in the neutral form, denoted by N⁰, is the same as that at the equilibrium N⁰_eq [13]. However, the ionized form (Eq. 4) appear at typical temperature above 250°C, which is considered as the dominant form [14-16]. Taking into account the assumptions listed above, the equation describing the sensor dynamics in oxygen atmosphere is given by:

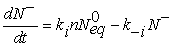(5)

N^– is the density of ionized oxygen and n the density of electrons given as a function of potential barrier V_b [17]

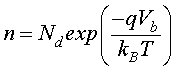(6)

V_b is the potential barrier in the grain boundary.

When carbon monoxide molecules are introduced, the dominant reaction is that occurring with the pre-adsorbed oxygen ions O^– to form CO2 molecule following the equation below [18,19]

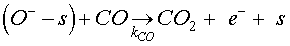(7)

K_CO denotes the constant of the reaction between the CO molecules and the ionized oxygen. For Eq.5, a desorption term caused by reducing gas must be added to take into account the reaction given by Eq. 7 [20]

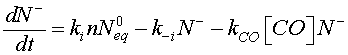(8)

[CO] denotes the carbon monoxide concentration. Using Eqs. 6 and 8, Eq. 12 can be modified as follow

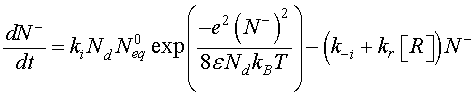(9)

The density of the ionized oxygen decreases when CO molecules is introduced. Then, the trap density will shift from the equilibrium value in air N^–_eq to a value N^– indicated by a decrease of the potential barrier [21]. The equilibrium state just before gas introduction is taken as a reference state and we define the effective recovery rate, 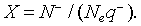This parameter gives an idea about the ability of the reducing gas to remove oxygen ions. Otherwise, using Eq. 5 at thermodynamically equilibrium just before gas exposure, Eq. 9 can be simplified by introducing χ Then, we find:

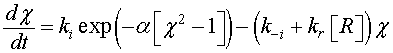(10)

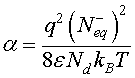is a dimensionless parameter which represents the potential barrier V_b⁰ and thermal voltage ratio. In order to solve Eq. 10, a linearization procedure based on the Taylor series expansion [22,23] is adopted to obtain more simplified equation.

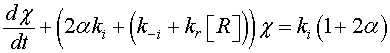(11)

The reaction constants are assumed to have the Arrhenius form and time independent. As a consequence, the solution of Eq. 11 is given by

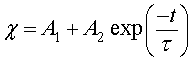(12)

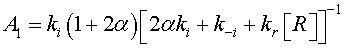
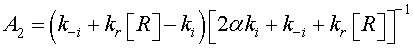
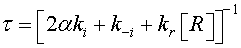
In the case of low CO concentrations and for a short time gas exposure, we can assume that 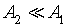.Then, the current density described by Eq. 2, can be expressed as:

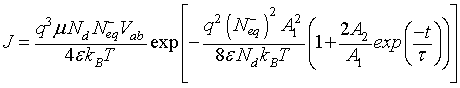(13)

It is worthy to note that for porous sensitive layers, the Pt electrodes do not affect the total resistance of sensitive layer [10]. However, the resistance would be influenced by typical morphology of the layer which includes the porosity, conduction channels for carriers transport and the layer dimensions (thickness, length…). The porosity and conduction channels can be described accurately by two morphological parameters: the contact area between neighboring grains and the density of grain boundary per unit area ρ_c. The contact area is assumed to be a circle with radius 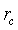The first parameter indicates the possibility of electrons to flow across the grain boundary. ρc represents the amount of conductive channels available for electrons. In this context, it is important for an accurate conduction model to consider the impact on these parameters in porous layers. For a single grain boundary, the surface seen by electrons when they drift from one grain to another is given by 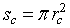. The total contact area in the plan perpendicular to current direction (Figure 2) is given by 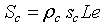, where L and e, are the length and the thickness of the sensitive layer respectively. For the sensitive layer S_c must be multiplied by n₁ the number of contacts in the current direction which can be determined using the mean grain size D and l, the width of sensitive layer. The total real contact area is given by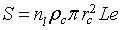

Thereby, the resistance for the whole sensitive layer is given by

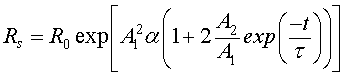(14)

where 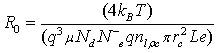denotes the initial resistance.

Results and Discussion

The responses of WO₃ gas sensor under CO were studied at 250°C. The morphology of WO₃ layer surface was studied. Figure 3 illustrates a SEM micrograph for the film surface, grain and contact width analysis.

Grain size analysis show that the mean size is about 165 nm. Considering the relative permittivity ε_r=5.24 and n_b=4 1021 m⁻³ for WO₃ thin films [24,25], the Debye length 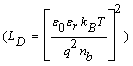at 250°C is 55 nm. In this case, the effect on the sensor resistance is dominated by the grain boundary potential barriers [10].

In the other hand, electrical measurements were carried under dry air and three concentrations of carbon monoxide 10, 30 and 90 ppm at 250°C. In a first step, I-V measurement were performed in the presence of dry air and carbon monoxide in order to verify that the electrodes do not affect the total resistance of the WO₃ sensitive layer. The sweep voltage was applied in the range of 0-4 V with step length 0.01 V/s.

The linear I-V curves of Figure 4 shows the Ohmic character between electrodes and sensitive layer. It should be noticed that linear I-V behavior was also observed for metal oxides and semiconductors [26,27].

The gas sensing properties of the WO₃ layer were observed by the resistance transients under different CO concentrations 10, 30 and 90 ppm with total flow rate 0.5 L/min. The time dependencies of electrical resistance were presented in Figures 5a-5c when the WO₃ sensitive layer was heated at 250°C. During the tests under carbon monoxide the bias voltage was kept constant at 0.1 V.

The analytical resistance (Eq. 14) was used to estimate N^–_eq. R₀ value and the contact radius r_c are obtained from Figures 5 and 3c respectively, the sensitive layer dimensions and associated calculated parameters such as the electron mobility (using the Einstein relation D = μk_bT/q. The other parameters were considered from values found in literature [15,24,28].

The set of parameters values used in the model can be summarized as follow (Table 1).

The calculated value of N^–_eq is found to be 1.4 10¹⁷m^-2. It should be noticed that N^–_eq must be less or equal to the total adsorption sites density which can be found in literature [15]. The obtained value of N^–_eq exhibited that the potential barrier V_b⁰ under dry air is 0.82 eV which is a typical value for metal oxide materials [29,30].

The others parameters, were estimated by fitting the experimental transients to Eq 14. The goodness of the fit was evaluated by minimizing the reduced chi-square value and minimize the difference between the simulated resistance R^s_si and the measured resistance R_si to obtain the optimal parameters values. The reduced chi-square is given by

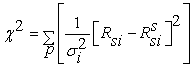
Where p is the number of data points and σ_i² is the variance related to the measurement error of R_si . The fitting process was achieved when the difference between two successive reduced chi-square values is less than a certain tolerance value. Thus the fit has been optimized when a value of 10^-9 of the chi-square tolerance was reached.

For the tested CO concentrations, the best estimated parameters are illustrated in Table 2.

Eq. 14 was fitted to the measured resistance transients (Figure 5) for different CO concentrations.

In the case of low gas concentration where [CO] =10 ppm and 30 ppm (Figures 5a and 5b), a good agreement between the fitted and measured resistances is observed, while for 90 ppm the agreement is less good. Since the present model is based on the assumption of low concentration, the disagreement seen in Figure 5c is probably due to the higher gas density at the sensor surface. In fact, when the CO molecules are introduced, they react with adsorbed oxygen according to Eq. 7 giving rise to a decrease in the potential barrier V_b which, in turn, causing the resistance to decrease. For high concentration this mechanism will continues; the density of electrons given in Eq. 6 increases which promotes the oxygen ionization process. The coexistence of these two processes will lead to a steady state which is limited by the presence of the CO molecules. Finally, when the reducing gas is removed then only the oxygen ionization process remains which increases the resistance of the sensitive layer.

Conclusions and Outlooks

The model proposed in this paper makes a convincingly results for transient modeling and gives an idea on how related parameters can influence the sensor response when exposed to the gas. These parameters can be estimated which allows us to predict some intrinsic properties of the sensitive layer. On the other hand, it should be noted that the good agreement of the fit with experimental results indicates that the model based assumptions are acceptable under the analyzed conditions. We show that fitting the presented analytical resistance to the experimental data allows calculation of several quantities that can be used for improving the sensor response. This model will serve as a base to explore and to interpret the recovery time after gas sensor exposure. Further work is in progress to extend its validity for more reducing gases (ethanol and acetone) and to show the effect of metallic additives on gas sensors responses to confirm the robustness of our model.

Acknowledgment

This work is partially supported by the French-Tunisian Cooperation PHC-Utique (Project 11/G 1301).

References

1. Simon I et al. Micromachined metal oxide gas sensors: opportunities to improve sensor performance. Sens. Actuators B 2001; 73: 1-26.
2. Korotcenkov G. Metal oxides for solid-state gas sensors: What determines our choice? Materials Science and Engineering B 2007; 139: 1-23.
3. Lee DD and Lee DS. Environmental gas sensors. IEEE Sensors Journal 2001; 1: 214-224.
4. Park CO and  Akbar SA. Ceramics for chemical sensing. Journal of Materials Science 2003; 38:  4611-4637.
5. Smith DJ et al. Wittman. Stability  sensitivity and selectivity of tungsten trioxide films for sensing applications. Sensors and Actuators B: Chemical 1993; 13: 264-268.
6. Penza M et al. Tungsten trioxide WO3 sputtered thin films for a NOx gas sensor. Sensors and Actuators B: Chemical 1998; 50: 9-18.
7. Nguyen T et al. Polycrystalline tungsten oxide nanofibers for gas-sensing applications. Sensors and Actuators B 2011; 160: 549-55.
8. Stoycheva T et al. Micromachined gas sensors based on tungsten oxide nanoneedles directly integrated via aerosol assisted CVD. Sensors and Actuators B  2014; 198: 210-218.
9. Orton JW and Powell MJ. Reports on Progress in Physics 1980; 43: 1263-1307.
10. Barsan N and. Weimar U. Conduction model of metal oxide gas sensors. Journal of Electroceramics 2001; 7: 143-167.
11. Blatter G and Greuter F. Carrier transport through grain boundaries in semiconductors. Phys Rev B 1986; 33: 3952-3966.
12. Taylor WE  et al. Grain boundary barriers in germanium. Phys Rev 1952; 88: 867-875.
13. Fort A  et al. Simplified models for SnO2 sensors during chemical and thermal transients in mixtures of inert. oxidizing and reducing gases. Sensors and Actuators B 2007; 124: 245-259.
14. Boudiba A et al. Sensing mechanism of hydrogen sensors based on palladium-loaded tungsten oxide Pd-WO3. Sensors and Actuators B. 2013;187: 84-93.
15. Guérin J, Bendahan M, Aguir K. A dynamic response model for the WO3-based ozone sensors. Sensors and Actuators B128 2008 462-467.
16. Chemical Sensors VI: Chemical and biological sensors and analytical methods: Proceedings of the International Symposium. The Electrochemical Society. 2004.
17. Yamazoe N and Shimanoe K. Theory of power laws for semiconductor gas sensors. Sensors. Actuators B 2008; 128: 566-573.
18. Hübner M et al. CO sensing mechanism with WO3 based gas sensors. Sensors and Actuators B 2010; 151: 103-106.
19.  Susanti D et al. Preparation of CO gas sensor from WO3 nanomaterial synthesized via sol-gel method followed by hydrothermal process. AIP Conf Proc 1586. 2014.
20. Fort A  et al. CO sensing with SnO2-based thick film sensors: Surface state model for conductance responses during thermal-modulation. Sens. Actuators B 2006; 116: 43-48.
21. Boudiba A et al.  Sensing mechanism of hydrogen sensors based on palladium-loaded tungsten oxide Pd-WO3. Sensors and Actuators B 2013; 187: 84-93.
22. Weltner  K et al. Mathematics for Physicists and Engineers. Fundamentals and Interactive Study Guide. Springer-Verlag Berlin Heidelberg. 2009.
23. Gajic Z. Linear Dynamic Systems and Signals. Prentice Hall 2003.
24. Labidi A et al. dc and ac characterizations of WO3 sensors under ethanol vapors. Sensors and Actuators B 2006; 116: 374-379.
25. D. Manno. A. Serra. M. Di Giulio. G. Micocci. A. Tepore. Physical and structural characterization of tungsten oxide thin films for NO gas detection. Thin Solid Films 324 1998 44-51.
26. Liu Z et al. Laser ablation synthesis and electron transport studies of tin oxide nanowires. Advanced Materials 20 2003 1754-1757.
27. Zhang D et al. Electronic transport studies of single-crystalline In2O3 nanowires. Applied Physics Letters 2003: 112-114.
28. Crandall RS and Faughnan BW. Measurement of the diffusion coefficient of electrons in WO3 films. Applied Physics Letters. 1975; 26:120.
29. Look DC et al. Electrical properties of bulk ZnO. Solid State Communications 1998; 6: 399-401.
30. Barsan N. Conduction models in gas-sensing SnO2 layers: grain-size effects and ambient atmosphere influence. Sensors and Actuators B: Chemical 1994; 6: 241-246.