ISSN ONLINE(2319-8753)PRINT(2347-6710)
ISSN ONLINE(2319-8753)PRINT(2347-6710)
| Usha Mittal1, Sanyam Anand2 M.Tech student, Dept. of CSE, Lovely Professional University, Phagwara, Punjab, India1 Assistant Professor, Dept. of CSE, Lovely Professional University, Phagwara, Punjab, India2 |
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology
De-noising and segmentation are fundamental steps in processing of images. They can be used as preprocessing and post-processing step. They are used to enhance the image quality. Various medical imaging that are used in these days are Magnetic Resonance Images (MRI), Ultrasound, X-Ray, CT Scan etc. Various types of noises affect the quality of images which may lead to unpredictable results. Various noises like speckle noise, Gaussian noise and Rician noise is present in ultrasound, MRI respectively. With the segmentation region required for analysis and diagnosis purpose is extracted. Various algorithm for segmentation like watershed, K-mean clustering, FCM, thresholding, region growing etc. exist. In this paper, we propose an improved watershed segmentation using denoising filter. First of all, image will be de-noised with morphological opening-closing technique then watershed transform using linear correlation and convolution operations is applied to improve efficiency, accuracy and complexity of the algorithm. In this paper, watershed segmentation and various techniques which are used to improve the performance of watershed segmentation are discussed and comparative analysis is done.
Keywords |
||||||
| De-noising, Segmentation, Watershed, Region merging, RAG, Morphological Operations. | ||||||
INTRODUCTION |
||||||
| Digital Image processing refers to processing of digital images by digital computers [1]. Now a day, in every field digital imaging is widely used. But image quality is major concern as various equipment errors, inefficiency and environmental factors degrade the quality of images by introducing noises in images. Noise is an unwanted signal present in the image but modifies the actual image content. But in most of areas like medical, satellite, pattern recognition etc. require images with zero tolerance to these noises. But it is not possibly to completely eliminate the noise but reduction can be done by applying various filters and then area which is needed for analysis purpose can be extracted from the image. Various filters that can be used for de-noising are median filter, wiener filter, hybrid filter, sobel operator etc. For segmentation watershed algorithm is discussed. But watershed algorithm suffers from over segmentation [5]. To remove over segmentation problem, various techniques are used i.e. marker controlled approach, region merging etc. The paper is organized as follows: first of all various de-noising techniques are discussed then Watershed algorithm combined with other approaches is discussed and after that Comparative analysis of various denoising and segmentation techniques is given. | ||||||
II. DE-NOISING OF IMAGES |
||||||
| De-noising refers to the process of eliminating unwanted signal from image. De-noising can be performed either in spatial domain or in frequency domain. Spatial domain refers to the image plane itself [1]. Image processing operations applied on image directly modify the pixels of image. Frequency domain refers to representation of image into various frequency bands. Various filters that are used for de-noising are mean filter, median filter, wiener filter, hybrid filter, modified hybrid filter. | ||||||
| A. Mean Filter | ||||||
| In this scheme, a 3*3, 5*5 or 7*7 kernel is used and scans over the whole image from left top corner to bottom right corner. Mean of all the pixels lying within window is calculated and then center pixel is replaced with calculated mean. Mean is calculated by adding all pixel values and divided by sum of kernel elements. Unpredictable results are produced at the boundary [1],[3]. To remove this problem either boundaries of image are appended with zero value or duplicate value as boundary value. But mean filter doesn’t produce acceptable results as it is not necessary all elements within window are close to each other. | ||||||
| B. Median Filter | ||||||
| In this filter, same 3*3, 5*5 or 7*7 mask is used. Center pixel is replaced with the median of pixels lying in kernel window [1][3]. Median is calculated by sorting all the pixel values and then taking the middle element. It is efficient than mean filter but boundary is preserved in same way as in mean filter. Median filter is efficient for reducing speckle noise and salt & pepper noise. | ||||||
| C. Wiener Filter | ||||||
| Wiener filtering is an inverse filtering technique which is used to recover blurred image and images corrupted with additive (Gaussian) noise [3]. It works in frequency domain. In this filter, it is assumed that signal and noise processes are second-order stationary. Wiener filter is slow as it is operated in frequency domain. But to increase the speed, inverse FFT of wiener filter is calculated to obtain the impulse response. Impulse response is truncated in spatial domain to generate convolution mask. Although performance of wiener filter is low in spatial domain as compared to frequency domain but speed is much higher. In wiener filtering, although MSE value is showing degrading results but visual representation of the image is better. | ||||||
| D. Hybrid Filter | ||||||
| In this filter, median and wiener filter are used. Noisy image is inputted to the median filter and output of median filter acts as input for wiener filter. This filter is used to reduce various noises like salt and pepper, Gaussian noise, impulse noise and blurring effect from images [4]. | ||||||
| E. Modified Hybrid Median Filter | ||||||
| In this filter, combination of mean and median filter is used. The way of calculating mean and median is as follows:Suppose for n*n kernel, following matrix is produced to calculate the value. | ||||||
 |
||||||
| First of all, find the mean of R (mean_r) values and mean of D (mean_d) values. Second, find the median (md) of pixels marked as D and central pixels C. Then calculate final median mm=median (mean_r, mean_d,md,C) and replace pixel Xi,j. This filter produces better results as compared to other filters [3]. | ||||||
| F. De-noising Using Morphology | ||||||
| For morphological operations, two types of images are required: the original image on which processing need to be done and a structuring element of a specific shape that will act as a parameter to operation. Most commonly used morphological operations are dilation and erosion. Basically erosion shrinks the image means decreases the pixel values of the image and dilation expands the image means increases the pixel values of image. Based on erosion and dilation, morphological opening and closing operations are performed. Morphological opening is erosion followed by dilation operation. Morphological closing is defined as dilation operation followed by erosion. Using morphological operations for de-noising, the main concern is to select the appropriate structuring element. Structuring element should be large for removing noise [2]. | ||||||
III. SEGMENTATION OF IMAGES |
||||||
| A. Watershed Algorithm | ||||||
| Watershed segmentation is region-based segmentation whose idea comes from geography. Watershed algorithm is based on the image representation in three dimensions: two spatial coordinates and intensity. For topographic interpretation, three types of points are considered: A) points which belongs to regional minima. B) Points where if water drop is placed, it will fall with certainty to single minima. C) Points at which water is likely to fall to more than one minimum [1]. Imagine the landscape is submerged in a lake, with holes pierced in local minima. Watershed lines are divide lines of the domains of attraction of rain falling over the region. Watershed algorithm provides the complete division of the image [6]. It shows the connected regions with enclosed boundaries of single pixel wide. Main disadvantage of this algorithm is over-segmentation. Due to over-segmentation, regions are not clearly visible and it is sensible to noise. Various approaches are used to eliminate over segmentation like marker controlled approach, region merging etc. | ||||||
| B. Approaches to Remove Over Segmentation | ||||||
| 1) Region Merging: Region merging depends upon two criteria: a) region model, describing each region with a set of features. b) Dis-similarity measure, difference in the intensity values of two regions or dis-similarity between pixels along the boundaries. Merging on the basis of intensity is done by Region Adjacency Graph (RAG). Merging on the basis of features is done by computing texture features of regions. | ||||||
| 2) Region Adjacency Graph (RAG): In this, graph structures are considered for implementation. Different regions are represented by nodes. Adjacency between regions is represented by drawing an arc. Dual RAGs are also commonly used in which nodes represent boundaries and regions are represented by arcs separating the boundaries. | ||||||
| Figure 1 shows the image consisting of 5 regions. Figure 2 shows the region adjacency graph of image shown in figure 1. This has 5 nodes representing 5 different regions and 12 arcs showing adjacency between 5 regions. Figure 3 shows Dual RAG of the same image. | ||||||
| Algorithm of RAG based on boundary pixels: | ||||||
| 1. Input an image and create its RAG. | ||||||
| 2. For each region Ri | ||||||
| a. Consider its neighbor region Rj. | ||||||
| b. If Ri and Rj are similar, merge them to one region and update RAG. | ||||||
| 3. Steps 2 and 3 will be repeated until no region will merge. | ||||||
| Similarity criteria: Two regions will be merged if boundary between them is weak [8]. | ||||||
| Algorithm for region merging based on intensity values: | ||||||
| 1. Calculate the size of each region say Ni. | ||||||
| 2. Calculate the mean intensity of each region Ri and and denote this by: | ||||||
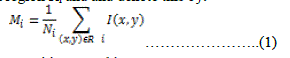 |
||||||
| 3. Define the criteria for two neighboring partitions I and j. | ||||||
| a. Calculate the difference in the mean intensities between two partitions say i and j: | ||||||
 |
||||||
| b. Calculate the difference in the intensities between two partitions: | ||||||
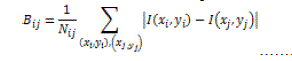 (3) (3) |
||||||
| 4. Calculate Cij for similarity measurement in intensity values between two partitions: | ||||||
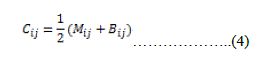 |
||||||
| Choose the threshold value Tc. If Cij is less than Tc then regions will be merged otherwise not [7]. | ||||||
| 3) Marker-Controlled Approach | ||||||
| In this approach, foreground and background markers are extracted. For foreground markers, morphological operations, “opening by reconstruction and closing by reconstruction” is used. In this erosion followed by dilation operation is performed. For finding good foreground markers regional maxima is calculated. For marking the background pixels, thresholding operation is performed which results the binary image. Then watershed ridge lines are calculated. After that we find regional minima in certain locations to modify gradient magnitude image so that regional minima occur at foreground and background pixels [5]. | ||||||
| 4) Modified Marker-Controlled Approach | ||||||
| In this rather than using morphological operations, simple convolution and correlation operations are used for finding the foreground and background markers [5]. In convolution, two arrays of different sizes are multiplied to get the third array. One mask or kernel is used to calculate the convolution. The mask is scanned over the whole image and the output pixel value is weighted sum of input array within the mask where weights are the values assigned in mask to each pixel of the window. Mathematically convolution can be defined as: | ||||||
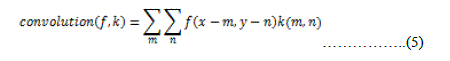 |
||||||
| Where f is the input image and k is the kernel of m*n size. | ||||||
| Convolution is equivalent to dilation in morphological operations | ||||||
| Correlation is almost similar to convolution, it is computed as a weighted sum of neighboring pixels. Weight matrix is known as correlation kernel which is 180 degree rotation of convolution kernel. Mathematically, it is defined as: | ||||||
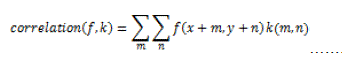 (6) (6) |
||||||
| Where f is input image and k is correlation kernel of mXn size. | ||||||
| Correlation is equivalent to erosion in morphological operations.. | ||||||
| This modified marker-controlled algorithm is much faster than morphological based algorithm. Speed and accuracy of this algorithm is more as compared to old algorithm [5] | ||||||
IV. COMPARISON OF VARIOUS DE-NOISING FILTERS |
||||||
V. COMPARISON OF VARIOUS SEGMENTATION ALGORITHMS |
||||||
VI. CONCLUSION AND FUTURE SCOPE |
||||||
| In this paper, we discussed about de-noising and segmentation techniques. As if segmentation alone is performed on the image, it does not produce acceptable results. So, to achieve better visualization of segmentation map, it should be pre-processed first to remove unwanted signals. It improves accuracy and helps in better interpretation. Final results obtained after segmentation depends upon the techniques applied for pre-processing of image, segmentation and postprocessing technique. | ||||||
ACKNOWLEDGMENTS |
||||||
| I would like to express my greatest gratitude to Mr. Sanyam Anand for his continuous support for the paper. | ||||||
Tables at a glance |
||||||
|
||||||
Figures at a glance |
||||||
|
||||||
References |
||||||
|