Moving Object Tracking in Video Sequence
Using Dynamic Threshold

V.Elavarasi; S.Ringiya; M.Karthiga

Moving Object Tracking in Video Sequence Using Dynamic Threshold

V.Elavarasi¹, S.Ringiya², M.Karthiga³

Assistant professor, Dept. of ECE, E.G.S.pillay Engineering College, Nagapattinam, Tamilnadu, India
UG Student, Dept. of ECE, E.G.S.pillay Engineering College, Nagapattinam, Tamilnadu, India
UG Student, Dept. of ECE, E.G.S.pillay Engineering College, Nagapattinam, Tamilnadu, India

Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Abstract

Most tracking-by-detection algorithms train dis-criminative classifiers to separate target objects from their surrounding background. In this setting, noisy samples are likely to be included when they are not properly sampled, thereby causing visual drift the multiple instance learning (MIL) paradigm has been recently applied to alleviate this problem However, important prior information of instance labels and the most correct positive instance (i.e., the tracking result in the current frame) can be exploited using a novel formulation much simpler than an MIL approach. In this paper, we show that integrating such prior information into a supervised learning algorithm can handle visual drift more effectively and efficiently than the existing MIL tracker. We present an online discriminative feature selection algorithm that optimizes the objective function in the steepest ascent direction with respect to the positive samples while in the steepest descent direction with respect to the negative ones. Therefore, the trained classifier directly couples its score with the importance of samples, leading to a more robust and efficient tracker. Numerous experimental evaluations with state-of-the-art algorithms on challenging sequences demonstrate the merits of the proposed algorithm.

Keywords

Object tracking, multiple instance learning supervised learning, online boosting.

INTRODUCTION

Object tracking has been extensively studied in computer vision due to its importance in applications such as automated surveillance, video indexing, traffic monitoring, and human-computer interaction, to name a few. While numerous algorithms have been proposed during the past decades it is still a challenging task to build a robust and efficient tracking system to deal with appearance change typically learn an appearance model and use it to search for image regions with minimal reconstruction errors as tracking results. To deal with appearance variation, adaptive models such as the WSL tracker and IVT method have been proposed.utilizen Several fragments to design appearance model to handle pose change and partial occlusion. Recently,sparse representation methods have been used to represent the object by a set of Target and trivial templates to deal with partial occlusion, illumination change and pose variation However, these generative models do not take surrounding visual context into account and discard useful information that can be exploited to better separate target object from the background. Discriminative models pose object tracking as detection problem in which A classifier is learned to separate the target object from its surrounding background within A local region. Collins demon state that selecting discriminative features in an online manner Improves tracking performance Boosting method has been used for object tracking by Weak classifiers with pixel based features within the target and background regions with the on-center off-surround principle.Grabner propose an online boosting feature selection method for object tracking. However, the above-mentioned discriminative algorithms utilize only one positive sample (i.e., the tracking result combing in the current frame and) multiple negative samples when updating the classifier. If the object location detected by the current classifier is not caused by abrupt motion, illumination variation, shape deformation, and occlusion (See Fig. 1). It has been demonstrated that an effective adaptive appearance model plays an important role for object tracking. In general, tracking can be categorized into two classes based on their representation schemes generative and discriminative models Generative algorithms precise, the positive sample noisy and result inupdate Consequently, errors will suboptimal be classifier accumulated be and cause tracking drift or failure [15]. To alleviate the drifting prob- lem, an online semi-supervised approach [10] is proposed to train the classifier by only labeling the samples in the first frame while considering the samples in the other frames as unlabeled. Recently, an efficient tracking algorithm [17] based on compressive sensing theories [19], [20] is proposed. It demonstrates that the low dimensional features randomly extracted from the high dimensional multiscale image fea-tures preserve the intrinsic discriminative capability, thereby facilitating object tracking.

PROPOSED METHOD

BLOCK DIAGRAM:

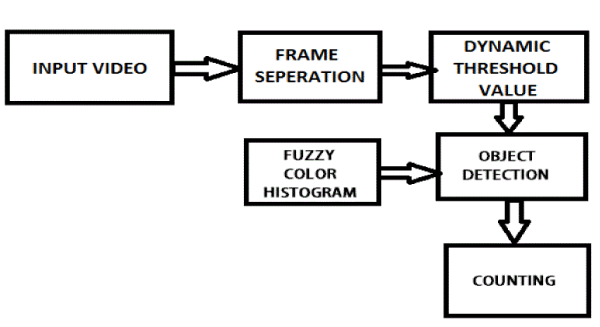We propose a simple and robust method for object detection in dynamic texture scenes. The underlying principle behind our model is that colour variations generated by background motions are greatly attenuated in a fuzzy manner. Therefore, compared to preceding methods using local kernels, the future method does not require estimation of any parameters (i.e.,nonparametric). This is quite advantageous for achieving the robust background subtraction in a wide range of scenes with spatiotemporal dynamics. Specifically, we propose to get the local features from the fuzzy colour histogram (FCH) . Then, the background model is dependably constructed by computing the similarity between local FCH features with an online update procedure. To verify the advantage of the proposed method, we finally compare ours with competitive background subtraction models proposed in the literature using various dynamic texture scenes.

FUZZY COLOR HISTOGRAM

In this paper, the colour histogram is viewed as a color distribution from the probability viewpoint. Given a color space containing color bins, the color histogram of image containing pixels is represented as , where is the probability of a pixel in the image belonging to the thcolor bin, and is the total number of pixels in the thcolor bin.According to the total probability theory,can be defined as follows:

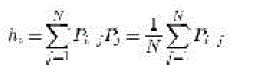Where Pj is the probability of a pixel selected from image I being the jth pixel, which is 1/N and Pi/j is the conditional probability of the selected th pixel belonging to the ithcolor bin. In the context of CCH, is defined as In the context of CCH, is defined as

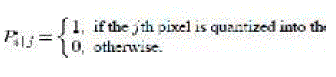This definition leads to the boundary issue of CCH such that the histogram may undergo abrupt changes even though colour variations are actually small. This reveals the reason why the CCH is sensitive to noisy interference such as illumination changes and quantization errors. The proposed FCH essentially modifies probability Pi|j as follows. Instead of using the probability Pi|j, we consider each of the N pixels in image I being related to all the color bins via fuzzy-set membership function such that the degree of “belongingness” or “association” of the th pixel to the ith color bin is determined by distributing the membership value of the jth pixel, , μij to the ith color bin.

DEFINITION (FUZZY COLOR HISTOGRAM):

The fuzzy color histogram (FCH) of image I can be expressed asF(I)=[f1,f2, f3,...... fn], where

ALGORITHM (FUZZY -MEANS):

Step-1: Input the number of clustersc, the wightingexponent,and error tolerance

Step-2: Initialisze the cluster centers vi, for 1 ≤i≤ c

Step – 3: Input data X= {x1, x2, .... xn} Step-4: Calculate the c cluster centers {vi(l)} by (6)

Step-5: Update U(l) by (7)

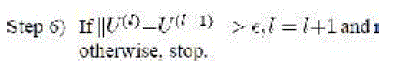In our work, we need to classify the fine colors in CCH into clusters for FCH. Due to the perceptual uniformity of CIELAB color space, the inner product can be simply replaced by , which is the Euclidean distance between the fine color and the cluster center . The fuzzy clustering result of FCM algorithm is represented by matrix , and is referred to as the grade of membership of color with respect to cluster center . Thus, the obtained matrix can be viewed as the desired membership matrix for computing FCH, i.e., . Moreover, the weighting exponent in FCM algorithm controls the extent or “spread” of membership shared among the fuzzy clusters. Therefore, we can use the parameter to control the extent of similarity sharing among different color bins in FCH. The membership matrix can be thus adjusted according to different image retrieval applications. In general, if higher noisy interference is involved, larger value should be used.

FUZZY MEMBERSHIP BASED LOCAL HISTOGRAM FEATURES

Fuzzy Membership Based Local Histogram Features The idea of using FCH in a local manner to obtain the reliable background model in dynamic texture scenes is motivated by the observation that background motions do not make severe alterations of the scene structure even though they are widely distributed or occur abruptly in the spatiotemporal domain, and color variations yielded by such irrelevant motions can thus be efficiently attenuated by considering local statist ics defined in a fuzzy manner, i.e., regarding the effect of each. Therefore, it is thought that fuzzy membership based local histograms pave a way for robust background subtraction in dynamic texture scenes. In this subsection, we summarize the FCH model and analyze the properties related to background subtraction in dynamic texture scenes.

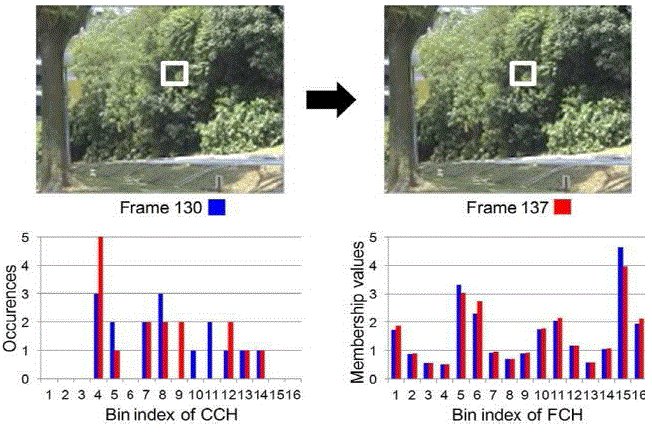First of all, in a probability view, the conventional colour histogram (CCH) can be regarded as the probability density function. Thus, the probability for pixels in the image to belong to the ith colour bin wi can be defined as follows:

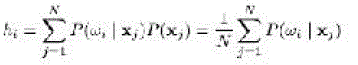where N denotes the total number of pixels. P(Xj) is the probability ofcolour features selected from a given image being those of the jth pixel, which is determined as

P(wi / Xj).

FCH bins. More specifically, the FCM algorithm finds a minimum of a heuristic global cost function defined as follows

LOCAL FCH FEATURES

In this subsection, we describe the procedure of background subtraction based on our local FCH features. To classify a given pixel into either background or moving objects in the current frame, we first compare the observed FCH vector with the model FCH vector renewed by the online update as expressed in (6):

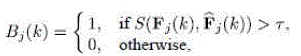Where Bj(k)=1 denotes that the th pixel in the th video frame is determined as the background whereas the corresponding pixel belongs to moving objects if.

B(j,k)= 0. τ is a thresholding value ranging from 0 to 1. The similarity measure used in (6), which adopts normalized histogram intersection for simple computation, is defined as follows:

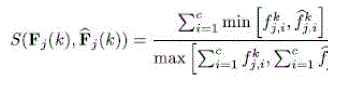Where denotes the background model of the th pixel position in the th video frame, defined in (8). Note that any other metric (e.g., cosine similarity, Chi-square, etc.) can be employed for this similarity measure without significant performance drop. In order to maintain the reliable background model in dynamic texture scenes, we need to update it at each pixel position in an online manner as follows:

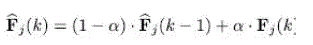Where is the learning rate. Note that the larger denotes that local FCH features currently observed strongly affect to build the background model. By doing this, the background model is adaptively updated. For the sake of completeness, the main steps of the proposed method are summarized in Algorithm

THRESHOLDING

A simple segmentation technique that is very useful for scenes with solid objects resting on a contrasting background. All pixels above a determined (threshold) grey level are assumed to belong to the object, and all pixels below that level are assumed to be outside the object. The selection of the threshold level is very important, as it will affect any measurements of parameters concerning the object (the exact object boundary is very sensitive to the grey threshold level chosen). Thresholding is often carried out on images with bimodal distributions. This is explained below. The best threshold level is normally taken as the lowest point in the trough between the two peaks (as above) alternatively, the mid-point between the two peaks may be chosen.

Figure 4 below illustrates the application of a thresholding algorithm on a sample image. It clearly identifies the objects of interest in the image, and removes any noise present.

MORPHOLOGICAL FILTERING

Morphological image processing is a collection of non-linear operations related to the shape or morphology of features in an image. Morphological operations rely only on the relative ordering of pixel values, not on their numerical values, and therefore are especially suited to the processing of binary images. Morphological operations can also be applied to grey scale images such that their light transfer functions are unknown and therefore their absolute pixel values are of no or minor interest.

Morphological techniques probe an image with a small shape or template called a structuring element. The structuring element is positioned at all possible locations in the image

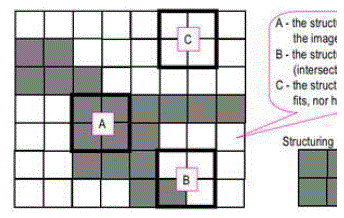and it is compared with the corresponding neighbourhood of pixels. Some operations test whether the element "fits" within the neighbourhood, while others test whether it "hits" or intersects

A morphological operation on a binary image creates a new binary image in which the pixel has a non-zero value only if the test is successful at that location in the input image.

The structuring element is a small binary image, i.e. a small matrix of pixels, each with a value of zero or one:

The matrix dimensions specify the size of the structuring element.

The pattern of ones and zeros specifies the shape of the structuring element. An origin of the structuring element is usually one of its pixels, although generally the origin can be outside the structuring element.

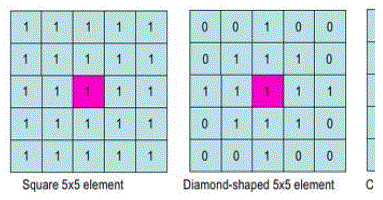A common practice is to have odd dimensions of the structuring matrix and the origin defined as the centre of the matrix. Stucturing elements play in moprphological image processing the same role as convolution kernels in linear image filtering.

When a structuring element is placed in a binary image, each of its pixels is associated with the corresponding pixel of the neighbourhood under the structuring element. The structuring element is said to fit the image if, for each of its pixels set to 1, the corresponding image pixel is also 1.Similarly, a structuring element is said to hit, or intersect, an image if, at least for image pixel is also 1.

SOFTWARE DETAIL MATLAB GUI

A graphical user interface (GUI) is a user interface built with graphical objects, such as buttons, text fields, sliders, and menus. In general, these objects already have meanings to most computer users. For example, when you move a slider, a value changes; when you press an OK button, your settings are applied and the dialog box is dismissed. Of course, to leverage this built-in familiarity, you must be consistent in how you use the various GUI-building components.

Applications that provide GUIs are generally easier to learn and use since the person using the application does not need to know what commands are available or how they work. the action that results from a particular user action can be made clear by the design of the interface the sections that follow describe how to create GUIs with MATLAB. This includeslaying out the components, programming them to do specific things in response to user actions, and saving and launching the GUI.

LITERATURE SURVEY

Background subtraction is a computational vision process of extracting foreground objects in a particular scene. A foreground object can be described as an object of attention which helps in reducing the amount of data to be processed as well as provide important information to the task under consideration. Often, the foreground object can be thought of as a coherently moving object in a scene.

There are many challenges in developing a good background subtraction algorithm. First, it must be robust against changes in illumination. Second, it should avoid detecting non-stationary background objects and shadows cast by moving objects.

CONCLUSION

In this paper we present a dynamic threshold optimization method for object tracking which couples the classifier score explicitly with the importance performance when compared with several state-of-the-art – algorithms.

References

M. Black and A. Jepson, “EigenTracking:Robust matching and tracking of articulated objects using a view-based representation,” inProc. Eur.Conf. Comput. Vis., Apr. 1996, pp. 329– 342.

Jepson, D. Fleet, and T. El-Maraghi, “Robust online appearance models for visual tracking,” IEEE Trans. Pattern Anal. Mach. Intell., vol.25, no. 10, pp. 1296–1311, Oct. 2003.

S. Avidan, “Support vector tracking,” IEEE Trans. Pattern Anal. Mach. Intell., vol. 29, no. 8, pp. 1064–1072, Aug. 2004.

R. Collins, Y. Liu, and M. Leordeanu, “Online selection of discriminative tracking features,” IEEE Trans. Pattern Anal. Mach. Intell., vol. 27, no.10, pp. 1631–1643, Oct. 2005.

M. Yang and Y. Wu, “Tracking non-stationary appearances and dynamic feature selection,” in Proc. IEEE Conf. Soc. Conf. CVPR, Jun. 2005, pp.1059–1066.

Adam, E. Rivlin, and I. Shimshoni, “Robust fragments-based tracking using the integral histogram,” in Proc. Comput. Soc. Conf. IEEE CVPR,Jun. 2006, pp. 789–805.