Research and Reviews - International Journals

International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Menu

ISSN ONLINE(2278-8875) PRINT (2320-3765)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

Multiple Cell Upsets Correction for OLS Codes

K.Michael Angelo1, P.Soundarya Mala2
  1. Student, Dept of Electronics and Communication Engineering, Godavari Institute of Engineering and Technology, A.P, India
  2. Assistant Professor, Dept of Electronics and Communication Engineering, Godavari Institute of Engineering and Technology A.P, India
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Abstract

An Error Correction code with Parity check matrix is implemented which is other type of the One Step Majority Logic Decodable (OS-MLD) called as Orthogonal Latin Squares (OLS) codes. It is a concurrent error detection technique for OLS codes encoders and syndrome computation because of the fact that when ECCs are used, the encoder and decoder circuits can also suffer errors.These OLS codes are used to correct the memories and caches. This can be achieved due to their modularity such that the error correction capabilities can be easily adapted to the error rate or to the mode of the operation.OLS codes typically require more parity bits than other codes to correct the same number of errors. However, due to their modularity and the simple low delay decoding implementation these are widely used in Error Correction. All the errors that affect a single circuit node are detected by the parity prediction scheme. The area and latency values are monitored.

Keywords
Concurrent error detection, error correction codes (ECC), Latin squares, majority logic decoding (MLD), parity, memory.

INTRODUCTION
The general idea for achieving error detection and correction is to add some redundancy which means to add some extra data to a message, which receiver can use to check uniformity of the delivered message, and to pick up data determined to be corrupt. Error-detection and correction scheme may be systematic or it may be non-systematic. In the system of the module non-systematic code, an encoded is achieved by transformation of the message which has least possibility of number of bits present in the message which is being converted. Another classification is the type of systematic module unique data is sent by the transmitter which is attached by a fixed number of parity data like check bits that obtained from the data bits. The receiver applies the same algorithm when only detection of the error is required to the received data bits which is then compared with its output with the receive check bits if the values does not match, there we conclude that an error has crept at some point in the process of transmission. Error correcting codes are regularly used in lower-layer communication, as well as for reliable storage in media such as CDs, DVDs, hard disks and RAM.
Provision against soft errors that apparent they as the bit-flips in memory is the main motto of error detection and correction. Several techniques are used present to midi gate upsets in memories. For example, the Bose–Chaudhuri– Hocquenghem codes, Reed–Solomon codes, punctured difference set codes, and matrix codes has been used to contact with MCUs in memories. But the above codes mentioned requires more area, power, and delay overheads since the encoding and decoding circuits are more complex in these complicated codes. Reed-Muller code is another protection code that is able to detect and correct additional error besides a Hamming code. But the major drawback of this protection code is the more area it requires and the power penalties.
Hamming Codes are mostly used to correct Single Error Upsets (SEU‟s) in memory due to their ability to correct single errors through reduced area and performance overhead. Although it is brilliant for correction of single errors in a data word, but they cannot correct double bit errors caused by single event upset. An extension of the basic SEC-DED Hamming Code has been proposed to form a special class of codes known as Hsiao Codes to increase the speed, cost and reliability of the decoding logic. One more class of SEC-DED codes known as Single-error-correcting, Doubleerror- detecting Single-byte-error-detecting SEC-DED-SBD codes be proposed to detect any number of errors disturbing a single byte. These codes are additional suitable than the conventional SEC-DED codes for protecting the byte-organized memories. Though they operate through lesser overhead and are good for multiple error detection, they cannot correct multiple errors. There are additional codes such as the single-byte-error-correcting, double-byte-errordetecting (SBC-DBD) codes, double-error-correcting, triple error-detecting (DEC-TED) codes that can correct multiple errors. The Single-error-correcting, Double-error-detecting and Double-adjacent-error-correcting (SEC-DED-DAEC) code provides a low cost ECC methodology to correct adjacent errors as proposed in. The only drawback through this code is the possibility of miss-correction for a small subset of many errors.
Error correction codes (ECCs) have been used to protect memories for many years. There are wide ranges of codes that used or proposed for the applications in the memory. The codes that can correct one bit per word called the Single error correction are commonly used known as SEC. More sophisticated studies are carried on the codes that correct the double adjacent errors or the double errors. Further the use of more complex codes that corrects more errors is limited by their impact on delay and power, which limits their applicability to the design of memory. To surmount the issues, the use of codes that are one step majority logic decodable (OS-MLD) has been proposed recently. OS-MLD codes can be decoded with low latency and so they are used for the protection of memories. Among the codes that are OS-MLD, a type of Euclidean geometry (EG) code has been proposed to protect memories. The use of difference set code has also been recently analyzed in. Another type of code that is OS-MLD is orthogonal Latin squares called the OLS codes. These got vast interest in memoires, caches and in interconnections. These require more parity bits than other codes even then these are widely used due to the fact that they are very modular which means the error correction capabilities can be adapted to the error rate without any difficulty or can also be tailored to the mode of operation. On the basis of specific properties of these codes, it is vivid that the parity prediction is an effective technique to detect errors in the encoder and syndrome computation. This is not the case for most other block codes for which parity prediction not able to endow with any efficient protection. Hence, this also adds as an benefit of OLS codes in addition to their modularity and the simple decoding.

OLS CODES
These are framed up on the perception of Latin squares. It is a matrix of the order „m‟ and have up to the permutations „m-1‟. When we super impose each diagonal pair elements they will show one time such a kind of squares are called the orthogonal ones. OLS codes we use in our scheme have data bits of number „m2‟. They have check bits of number “2tm” in which, „t‟ stands for numeral of errors such that code corrects. If we wanted to correct a double bit then we have „2‟ as the value of t and thereby the check bits required are 4m.By the knowledge of the construction which is quite modularity, we want to achieve which corrects „t+1‟ we can get by addition of 2m check bits to our code. By that property we can select the capability in order to correct the error for a desired word sizes. We can decode it by using MLD because 2t check bits involve. Hence the process is made easy when below„t‟. More or less t-1 check bits are required when utmost the digit of errors will be t or less. At any later case we could decode by the recompilation of parity check bits and could be checked together with the store parity bits.
The „H‟ matrix for OLS codes is build from their properties. The matrix is capable of correcting single type error. By the fact that in direction of the modular structure it might be able to correct many erros. They have check bits of number “2tm” in which, „t‟ stands for numeral of errors such that code corrects. If we wanted to correct a double bit then we have „2‟ as the value of t and thereby the check bits required are 4m.
the H matrix , of Single Error Code „OLS‟ code is construct as :
a. In the above, I2m is the identity matrix of size 2m.
b. M1, M2 are the matrices of given size m × m2.
„‟The matrix M1 have m ones in respective rows. For the r th row, the 1‟s are at the position (r − 1) × m + 1,(r − 1)× m + 2,………….(r − 1) × m+ m − 1, (r − 1) × m + m”
. The matrix M2 is structured as:
For the given value 4 for m, the matrices M1 and M2 can be evidently experiential in Figure 1.
H Matrix in the check bits we remove is evidently the G Matrix.
On concluding the above mentioned, it is evident that the encoder is intriguing m2 data bits and computing 2tm parity check bits by using G matrix . These resulted from the Latin Squares have the below properties:
a. Exactly in 2t parity checks each info bit is involved.
b. Utmost one in parity check bits info bits takes participation.
We use the above properties in the later section to examine our proposed technique.

PROPOSED TECHNIQUE
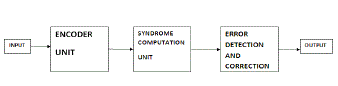
A self checking circuit is the foremost one we use in our proposed module. The circuit receives only a severance of the input space which may be called input code space in then produces output space named as output code space.
Assuming to be fault set we intend it as a self or auto checked. Lets assume F represents stuck-at fault model. If both the properties of (a)self-testing and (b)fault secure any circuit meets the both conditions we call them as self-testing. „F‟ is such a type when it meets the criteria that are all the fault f should be present in the sets of F in which even one of the input must be from the input code which is a prerequisite condition for freedom, for which the circuit is providing a production of output spaces.
If any circuit gives the correct output in spite of any given codes of the F then we call it as a fault-secure set it produces a perfect output which is of the o/p error spaces. It guarantee that the response that obtained is true. Else signals the existence of a fault. These can be identified every time as the i/p is present which yields o/p that will help in identifying their existence. The circuit receives only a severance of the input space which may be called input code space in then produces output space named as output code space. The gap among their occurring of faults is sufficient for permitting every element belonging to the input the modularity is related to this. Hence an error space belonging to the output will be seen near the circuit former to the incidence of the 2nd fault. The famous technique and sophisticated for noticing errors in simple common logic circuit is the addition of bits called the parity by the name parity prediction. The trouble we face is not complex forth encoder. The ci bits are compared with all of the checking equations which we got from the computational analysis. Hence CED system can be checked by c1 ^ c2 ^ c3 ^・ ・ ・^c2tm = 0. By the advantage we could implement proficiently compared with the rest techniques. If we see in Haming codes has the odds weight the required number is large since it has the odd weights. In our proposed the input code spaces replicas to their spaces, due to the fact that encoder takes deliveries of every 2k configurations. Further liability that occurring in a gate adjusts utmost the other check bits ci . If this happens with the alteration the provision of the output that won‟t gratify which means belonging to the output error space. Fault security chattels are guaranteed. The gap among their occurring of faults is sufficient for permitting every element belonging to the input the modularity is related to this. The r1,r2 outs are of the parities two disjoint subsets. If we give the right uniformity the code we get will take 00 or 11.The method we used could detects all the erroe that might effects the odd figure containing ci bits. We share at the centre or in between working out of ci bits. The promulgation considering for grater to ci bits also if it is even we might not find errors only in that situation. For overcoming this situation the area required for the circuit is being increased further no judgment share can be allow. Alternatively controlling common sense error may promulgate to odd ones. It reflects by sustained increase of expense and also unexpected completion. In add on if the error propagate impediment for every path might be diverse. By leading to these situations we might get few outputs with error near the clk. These facts guarantee the presence of the non share in the midst. In advancement of the technique might be able in finding every error that can be on circuit node. To revise the syndrome computation, the similar prediction implants as following
si---- computed syndrome bits.
Self checking Syndrome Computation;
It is for the code with k=16 also t as 1. The input coded spaces is the separation of probable 2k+2tm arrangements. In these situations we calculate utmost till t. Beyond that any deflection or errors might be crept in the circuit so we us the generated till the value of t. We pre arrange with OLS code word of valid and non valid type which will be to far at t or even lesser words. These all commune with input that is in which either no even a error or utmost t are able to being rectified. The space of the obtained calculation might compose on the requirement that both r1, r2 must be equal from the above two equations running at a condition go together output space. We use XOR gates in calculation of r1,r2 and not allocation any gates but comprising of the circuits. And hence one fault might proliferate to an out and yield in the error output spaces dividedly. We can show that it is a auto-testing possessions for sync calculations we should assume that an error might have crept in any one among all other gates from the working outs. We get all the conditions bits reflecting of the value 0 for a given valid OLS word we took then it shows there is a stuck-at fault 1 in our exclusions. If we take the similar condition but with a non of the type code word will exaggerates of the value or even it may be less while the sync nits are 1 which there by leads to sa0 faults which is clearly seen. We check 2tm bits further any of the fault might occur or be active the propagation to r2 is done quicker when compared to all of the situations. This enables a proficient implementation that is not probable in other codes. For example, in a Hamming code a important part of the columns in G has an odd weight and for a number of codes the number is even larger as they are intended to have odd weights. The input code spaces of the OLS encoder correspond to the input space, since the encoder can take delivery of all the possible 2k input configurations. The output code space of the OLS encoder is collected by the outputs satisfying (4), while the output error space is the balance of the output code space.
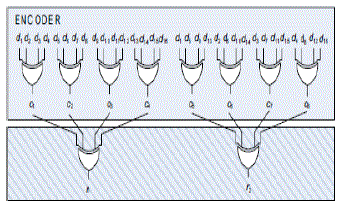
We have 2tm parity check bits to calculate the coded with k as m2 which has m-1 2 input XOR gates further preceding. Encoder needs 2tm(m-1) similar gates for the obtaining of the sync. Further calculation requires one add on XOR gate for every parity check bits.
For implanting our method we need overhead:
a. Encoder
b. Syndrome computation is

Detection of errors
In the propose method we are detect the errors by using syndrome computation bits.
Here we are checking the syndrome bits
All syndrome bits from S1 to S8 are zeros in our output do not have any errors.
Otherwise we are checking in syndrome computation bits having one or more number of one‟s in our output having errors.

Error Correction
In the proposed technique we are correct the single bit error
For example S1, S5 syndrome computation bits are one‟s remaining all syndrome bits are zeros in this case the d1 value is error to correct the d1 value to invert the d1 value.
For example S1, S6 syndrome computation bits are one‟s remaining all syndrome bits are zeros in this case the d2 value is error to correct the d2 value to invert the d2 value.
For example S1, S7 syndrome computation bits are one‟s remaining all syndrome bits are zeros in this case the d3 value is error to correct the d3 value to invert the d3 value.
For example S1, S8 syndrome computation bits are one‟s remaining all syndrome bits are zeros in this case the d4 value is error to correct the d4 value to invert the d4 value.
For example S2, S5 syndrome computation bits are one‟s remaining all syndrome bits are zeros in this case the d5 value is error to correct the d5 value to invert the d5 value.
For example S2, S6 syndrome computation bits are one‟s remaining all syndrome bits are zeros in this case the d6 value is error to correct the d6 value to invert the d6 value.
The remaining bits are also same procedure to correct the error bit.

SIMULATION RESULTS
Block diagram RTL schematic
Technology schematic
Design summary
Simulation output

CONCLUSION
By the vivid conclusion, an CED method to serve OLS codes encoders and their calculation was projected. This projected method had from the properties of OLS codes for designing a parity prediction scheme which is able to professionally implement and also could detect every errors that will have effect an only circuit nodes. In this brief, a CED method for OLS codes encoders and syndrome calculation was proposed. The proposed method took advantage of the property of OLS codes to design a parity prediction scheme that could be professionally implement and detects all errors that affect an only circuit node. Here proposed scheme to detect the one or extra errors and to correct the single bit errors by using Orthogonal Latin square error correcting technique. The method is applied for different word sizes there by resulted that the overhead will be small irrespective of how larger words we take. It is attractive even if very are being used say for instance in case of the caches the OLS code has sophisticatedly used in coming times. In the future to check error we need a momentous delay even though their brunt on access point in time can be shortened.

Figures at a glance
Figure Figure Figure
Figure 1 Figure 2 Figure 3
 

References