International Journal of Innovative Research in Science, Engineering and Technology

International Journal of Innovative Research in Science, Engineering and Technology

Menu

ISSN ONLINE(2319-8753)PRINT(2347-6710)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

N Policy For Repairable Bulk Arrival Queueing Model With Setup, Second Multi Optional Service Facility Under Restricted Number Of Server Vacations

M.I,Afthab Begum,k1 , Fijy Jose P2, ShanthiE3
  1. Professor, Department of Mathematics, Avinashilingam University, Coimbatore, Tamil Nadu, India
  2. Research Scholar, Department of Mathematics, Avinashilingam University, Coimbatore, Tamil Nadu, India
  3. Research Scholar, Department of Mathematics, Avinashilingam University, Coimbatore, Tamil Nadu, India
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology

International Journal of Innovative Research in Science, Engineering and Technology

Abstract

This paper analyses a repairable batch arrival queueing model with a second multi optional service(SOS) channel under N policy in which the server takes restricted number of multiple vacations during his idle period.The server leaves the system for vacation as soon as the system empties and after returning from vacation if the server finds N or more customers in the system then he immediately starts the setup work. Otherwise he repeats his vacation until he finally finds at least N customers or returns to the system after taking L vacations.ie At the end of Lth vacation if the server finds less than N customers he joins the system and stays idle until the queue length reaches at least N to start the setup work. After the completion of setup work, busy period initiates.The server may undergo unpredictable breakdowns during the service and sent for repair immediately.As soon as the repair is completed, the server returns to the customer whose service was interrupted. The system size distribution at a random epoch and mean system length are calculated and the corresponding results for the classical single and multiple vacation models are obtained as special case.

Keywords
Npolicy, Bulkarrival, Second multi optional Service, Restricted Vacation.

INTRODUCTION
The single and multiple vacation N-policy queueing models allow the server to take vacations whenever the system becomes empty.In the case of single vacation model the server after returning from the vacation joins the system even if the required number of customers are not present.That is ,the server stays idle in the system after returning from vacation until atleast N customers accumulate.In the case of classical multiple vacation the server may take unlimited number of vacations before joining the system.In the present paper a modified multiple vacation policy is considered,where the server takes atmost J vacations repeatedly until atleast N customers accumulate for service.If the number of arrivals does not reach N at the end of Jth vacation,then the server joins the system and remains idle until the number of arrivals in the queue reaches N.Thus the present paper is a generalization of the classical single and multiple vacation models.Also the second optional service considered in the present model consists of multi c-optional services so that the customer who completes the First Essential Service (FES) may choose the ith optional service with probability ri (or) leaves the system with probability (1-r) where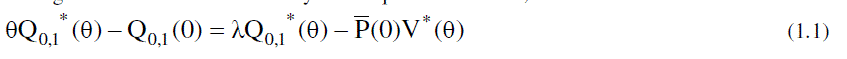image The server undergoes unpredictable breakdown during service and resumes his work after undergoing the repairwork.It is also assumed that the server does some preparatory work before starting the FES of each cycle.

II. RELATED WORK
In classical single server queueing models an idle server will start the service as soon as a customer enters to the empty system. But in many situations it is important to decide when the server should start his service ,as frequent setup inevitably make the operating cost too high. The N policy introduced by Yadin and Naor (1963) is the most general control policy in which the server does not start his service until there are N customers in the queue. This minimizes server switch overs and avoids excessive frequent use of setups. The N policy queue have been widely used to provide stochastic modelling of many problems arising in production inventory system, in telephone switching system and in quality control problems. The study of the N policy M/G/1 queueing system was first analysed by Heyman(1968) and was developed by several researchers such as Wang and Ke(2002) .In recent years,queues due to server vacations have emerged as an important area of queueing theory and have been studied exhaustively and successfully, in various applications. At present most of the studies are developed for batch arrival vacation models under various vacation policies. The first study of vacation models with N policy was done by Kella(1989).The various extensions of the vacation models under N policy can be referred to Lee et al.(1994,1995),Ke(2001) and others. Later Ke et al.(2010) studied the operating characteristics of an M/G/1 queueing system with a randomized control policy and at most J vacations.Queueing models with server breakdowns are more realistic representation of systems.The server may undergo unpredictable breakdowns during the service and sent for repair immediately.As soon as the repair is completed, the server returns to the customer whose service was interrupted. Discussing queueing systems with N policy and server breakdowns,Wang(1995) first proposed Markovianqueueing system under N policy and server breakdowns and derived analytical steady-state solutions of the N policy M/M/1 queue.Wang and Ke(2002) analysed the control policy for M/G/1 queueing system with an unreliable server.The N policy Markovian system with finite capacity and a non-reliable server was proposed by Wang and Hisch(1995).Recently Ke,Huang,Pearn(2010) has studied randomized policy of a poisson input queue with J vacations.Further Ke,Huang,Pearn(2010) discussed the randomized vacation policy for a batch arrival queue.Later Huang,Pearn(2011) analysed performance measures and randomized optimization of unreliable server MX/G/1 vacation system.In classical repeated vacation, the server takes infinite vacations which is unrealistic.Thus the server can be restricted to have atmost L vacations in one cycle.The L vacation queueing system can be considered as generalization of single and multiple vacation when L=1 and L=  . In the present paper the authorsanalyse the N policy of repairable batch arrival queueing system with general setup time in which the service discipline involves more than one service, of which one is essential and the other is multi optional .The server takes at most L vacations whenever the system becomes empty. The PGF of the steady state system size probabilities is obtained in a closed form so that various performance measures can be calculated easily.

III. MATHEMATICAL ANALYSIS OF THE SYSTEM

MODEL DESCRIPTION:
Arrival Pattern: Present Paper considers an Mx/G/1 queueing system where the arrivals occur in batches according to a compound Poisson process with random batch size X, group arrival rate λ and probability distribution gk=Pr(X=k) k=1,2,3,...Arriving customers form a single waiting line and the service is done one by one.
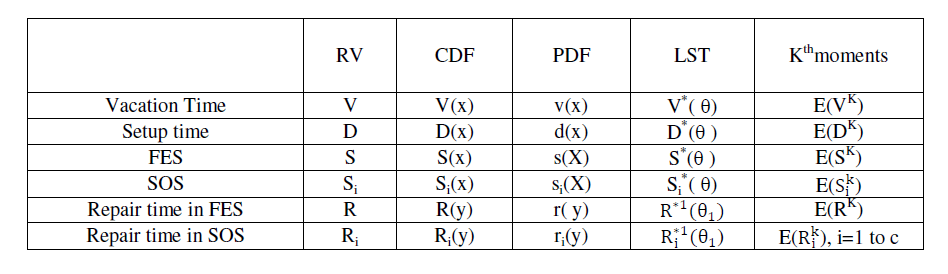
Vacation Policy: The server is turned off and leaves the system for vacation of random length V as soon as the system empties. After returning from the vacation if the server finds less than N customers he repeats his vacation until he finds at least N customers or returns to the system after taking L vacations. The vacation times are assumed to be iid with general distribution V (t).At the end of Lth vacation if the server finds less than N customers he joins the system and stays idle until the queue length reaches at least N.On the other hand if on returning from vacation the server finds N or more customers in the system, he immediately starts preparatory work which corresponds to the setup time. Setup time follows general distribution D(t).At the end of the setup operation the server begins to serve the customers exhaustively.
Busy Period: During busy period, the server provides single First Essential Service(FES) to all the arriving customers in the first phase and “multi-optional “service in the second phase. The multi-optional service consists of c types of heterogeneous service. As soon as the FES is completed, the customers may either leave the system or opt for any of the c services in the second phase . It is assumed that, the probability that the customer opts the ith type(1 ≤i≤c) of 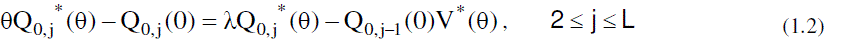image
Breakdown and Repair Period: It is assumed that the breakdowns occur during the services and the server’s life times are assumed to follow exponential distributions with mean1/a in FES and 1/aiinith SOS service. Whenever the breakdowns occur, the server issent for repair immediately and the customer just being served, waits in the service facility for the server to return from repair facility to complete the remaining service. The repair timesRandRi (i = 1toc) are arbitrarily distributed with probability distribution functionsR(y) andRi(y), density functions r(y) andri(y) and the first and second moments E(Ri k), k = 1, 2 and i=1 to c are the breakdowns occur in FES and SOS .Immediately after the server is fixed, the customer waiting in the service facility is taken up for service. Further, it is assumed that the service time for a customer is cumulative and after repair, the server is as good as new.
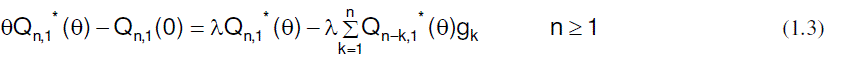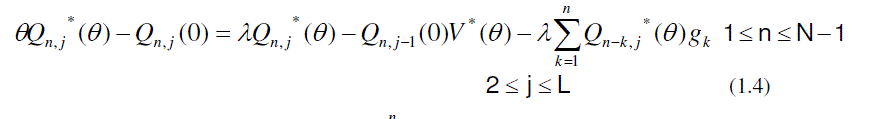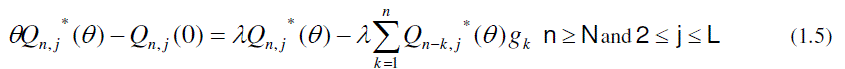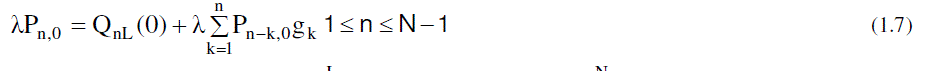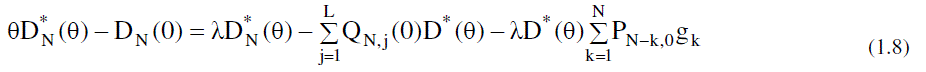image
image
image
image
image
image
image

Probability Generating Function
Now to obtain the partial PGFs of the number of customers in the system, the following partial PGFs are defined.
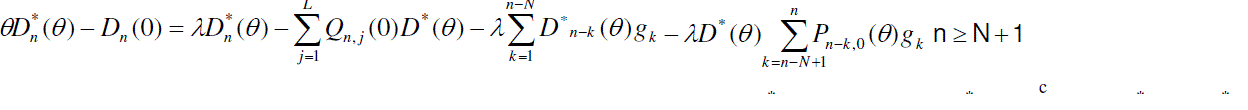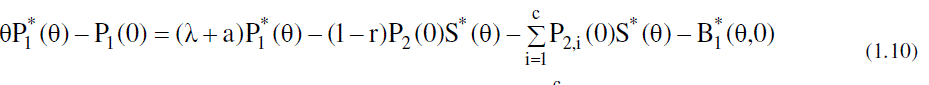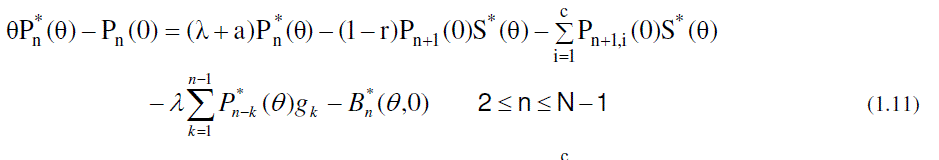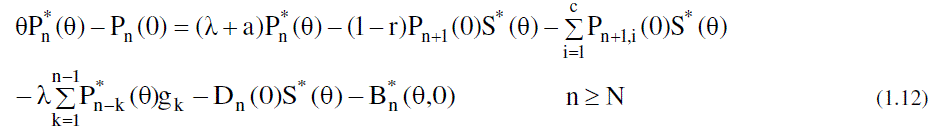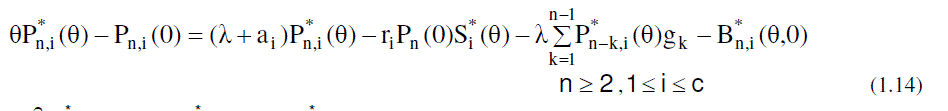image
image
image
image
image
image

V. CONCLUSION
It is verified that the model under consideration is the most generalization of N policy queueing models with server single and multiple vacation.It is noted that L=1 and L→∞ the re`sults of the proposed model coincide with thecorresponding results of the classical vacation N policy queueing models of Lee et al.(1995) and Lee et al.(1994) respectively.

References
  1. Cox.D.R1955The analysis of Non-Markovian stochastic process by the inclusion of supplementary variables Proceedings Cambridge Philosophical Society51433-441
  2. G, Choudhury, & M, P. (2006). A batch arrival queue with a second optional service channel under N policy. Stochastic Analysis and Applications, 24, 1-21.
  3. Gross, D., & C.M., H. (1998). Fundamentals of queueing theory. John Wiley,Newyork .
  4. Heyman, D. (1968). Optimal operating policies for M/G/1 queueing system. Oper.Res., 16, 362-382.
  5. Ke, J. (2001). The control policy of an Mx/G/1 queueing system with server startup and two vacation types. Math.Meth.of Oper.Reser., 54, 471- 490.
  6. Ke, J., & K.H., W. (2002). A recursive method for the N policy G/M/1 queueing system with finite capacity. European journal of Operations Research, 142, 577-594.
  7. Ke, J., K.B., H., & W.L., P. (2010). Randomized policy of a poisson input queue with J vacations. J Syst Sci Syst Eng, 19 (1), 050-071.
  8. Kella, O. (1989). The threshold policy in the M/G/1 queue with server vacations. Naval Research Logistics, 36, 111-123.
  9. Lee, H., S.S, L., & K.C., C. (1994(a)). Operating characteristics of Mx/G/1 queue with N policy. Queueing system, 15, 387-399.
  10. Lee, H., S.S., L., J.O., P., & K.C., C. (1994(b)). Analysis of Mx/G/1 queue with N policy and multiple vacations. J.aappl.Prob, 31, 467-496.
  11. S.S, L., H.W, L., S.H, Y., & K.C, C. (1995). Batch arrival queue with N policy and single vacation. computers and Operations Research, 22, 173-189.
  12. Wang, K., & J.C., K. (2002). Control policies of an M/G/1 queueing system with a removable and non reliable server. Int.Trans.Oper.res., 9, 195-212.
  13. Yadin, M., & P, N. (1963). Queueing system with a removable service station. Oper.Res., 14, 393-405.
  14. Wang, & K. H (1995). Optimal operation of a Markovian queueing system with a removable and non reliable server. Micro electronics Reliability, 35, 1131-1136.
  15. Wang, K .H, Hisch, & W.F. (1995). Optimal control of a removable and non-reliable server in a Markovian queueing system with finite capacity. Micro electronics Reliability, 35(2), 189-196.
  16. Wang, K., & J.C., K. (2002). Control policies of an M/G/1 queueing system with a removable and non reliable server. Int.Trans.Oper.res., 9, 195-212.
  17. Jau-Chuan, K., Kai-Bin, H., & Wen Lea, P. (2011). The performance measures and randomized optimization of unreliable server Mx/G/1 vacation system. Applied Mathematics and Computation , 217, 8277-8290.
  18. Ke, J.-C., Kai-Bin, H., & Wen Lea, P. (2010). The randomized vacation policy for a batch arrival queue. Applied Mathematical Modelling , 34, 1524-1538.