International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Menu

ISSN ONLINE(2278-8875) PRINT (2320-3765)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

Network Data Security Using FPGA

Ms.P.Thamarai #1, Mr.B.Karthik #2
  1. Assistant Professor, Dept of ECE, Bharath University, Chennai.,Tamil Nadu, India
  2. Assistant Professor, Dept of ECE, Bharath University, Chennai.,Tamil Nadu, India
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Abstract

This paper approaches a new and simple technique to develop the RSA algorithm using FPGA that can be used as a standard device in the secured communication system. This RSA algorithm is implemented in the FPGA with the help of VHDL. A simple nested loop addition and subtraction have been used in order to implement the RSA operation. This results in very low frequency requirement to perform this operation with consideration of high speed by reducing the gate counts with low power consumption of whole circuit, multiple key size support and low cost compared to earlier methods. The information to RSA encryption side is in the form of statement and the same will appear in the decryption side and its real time input/output also achieved effectively. The hardware design is targeted on Xilinx Spartan 3E device and it supports lower versions as well. The RSA algorithm design has made use of 951 total equivalent gate counts and achieved a clock frequency of 35.00MHz.

Keywords
Cryptography, FPGA, VHDL, Security, Communication.

INTRODUCTION
The immense advancement in network technology has resulted in great potential for changing the way we communicate and do huge business over the internet. But, for handling confidential data, the cost-effectiveness and globalism provided by the internet are reduced slowly by the main disadvantage of public networks. The expressively increasing growth in the confidential data traffic over the internet makes the security issue a fundamental problem. With this increasing demand of security in the communication channel, the development of a new, simple and efficient hardware security module has become the primary preference.
Wide varieties of works have been done on this particular field of hardware implementation of RSA algorithm to secure the data in different formats so far but not ended. A hardware implementation of RSA scheme has been proposed by Hani, et al. where they use Montgomery algorithm. A similar way has been taken by Kim, et al. This design scheme targets on the implementation of a 1024-bit RSA cryptographic processor. But both these designs have the drawbacks of slower processing time, though they use a faster clock and data handled only in binary or hex formats. An altered approach has been taken by Chris, et al. But, it does not provide the flexibility of using many practical applications as it can only be implemented with a fixed key size. Ibrahimy, et al. have proposed to implement RSA algorithm with flexible key size along with low clock frequency. But they also handled data in binary or hex format i.e. no real time output achieved and number of gates also high and in turn increase the power consumption.
This work approaches hardware implementation of RSA algorithm scheme using the modular exponentiation operation. Simple nested loop addition and subtraction have been used to implement the modular exponentiation operation. And to implement this, only shift registers, XORs and LUTs are used. The usage of NAND gate is avoided to reduce the complexity of the circuit by employing with reusability characteristics of XORs. Here, it supports multiple key sizes for RSA according to the application requirement. This new approach helps to reduce the system processing time, gate counts, frequency requirement and power consumption. And also the system could take the information in the form of statement say word format (real time input/output) not in binary or hex format as the earlier approaches handled.

DESIGN OVERVIEW
A distinct feature that can be found in the RSA algorithm [6] is that it concedes most of the integral part used in encryption to be re-used in the decryption process, which can decrease the resulting hardware area. In RSA, a plaintext block M is encrypted to a cipher text block C by:
The plaintext block is recovered by:
RSA encryption and decryption are mutual inverses and commutative as shown in equation (1) and (2), due to symmetry in modular arithmetic. One of the potential applications for which this design of RSA has been targeted is the secured data communication. In this application, the data input could be a statement which is fed into FPGA board directly via serial communication. The encryption module takes care of the security. The process at the receiving end is same as the process that has been followed at the sending end except that the sequence of the module is reverse. The RSA covers both the operation of encryption and decryption.
A. Fundamental RSA process
The RSA algorithm needs estimation of the modular exponentiation, which is separated into a series of modular multiplications by the application of exponentiation inquiring. The RSA encryption process is the mathematical operation, c = me mod n [6]. This mathematical operation has involved a few modular operations like modular-exponentiation, multiplication, addition and subtraction process on large integers [7]. Detail algorithms of the above operations for hardware implementation have been discussed in the following sections.
B. Modulus Exponentiation Process
The modular exponentiation operation is simply an exponentiation operation where multiplication and squaring operations are modular. The exponentiation operation developed for computing Me are applicable for computing Me(mod n). In the concern of hardware implementation, a clever algorithm is required in order to extent a superior efficiency. Hence, exponentiation is acquired by doing a number of squaring and multiplications.
C. Modular Multiplication Process
The modular multiplication problem is defined as the computation of P =(A x B) (mod n), given the integers A, B, and n. It is usually assumed that A and B are positive integers with 0 ≤ A, B < n.
The modulus multiplication operation is required after the separation of exponentiation into a number of squaring and multiplication. There are basically four general approaches for computing the product. Multiply and then divide, Interleaving multiplication and reduction, Brick ell’s method and Montgomery’s method.
All the above approaches have a common disadvantage that it doubles up the number of bits for each multiplication. For example, when two 32-bit numbers are multiplied together will cost a 64-bit result and hence a large register is needed to store this result.
A modified algorithm is used in this design which will be discussed later. The modified algorithm overcomes the problem by separating the multiplication operation into a number of modular addition operations.
D. Modulus Addition Process
The modular addition problem is defined as the computation of S = (A + B) (mod n) given the integers A, B, and n. It is usually assumed that A and B are positive integers with 0 ≤ A, B < n. The most common method of computing S is as follows:
1. Compute S = A + B.
2. Then S = S - n.
3. If S ≥ 0, then repeat step 2, else S = S.
Note that modular addition involves subtraction operation in step 2.
E. Complete Algorithm
The difficult part of RSA encryption/decryption lies on the modulus calculation of c = me mod n, to get the encrypted message “c”. To calculate the encrypted message “c”, it involves exponentiation that requires large amount of combinational logic, which increases exponentially with the number of bits being multiplied.
The possible way to accomplish this is by using a sequential circuit, which implements the exponentiation as a series of multiplications, and multiplication could also be implemented as a series of shifts and conditional additions [5] which has already been discussed in Section B and C where an exponentiation is separated into a number of multiplications and squaring. Each multiplication can be realized by a series of additions which has been discussed in Section D. To reduce the hardware size, modulus (mod n) is performed as a number of subtractions inside the multiplication loops. i.e. for each loop in addition, the divisor or modulus is subtracted from the engaged result whenever the engaged result becomes bigger than the divisor, and leaving the modulus when encryption is done. Then, the VHDL code for RSA design has been developed based on the new and simple technique. The VHDL code for data control, UART and device drivers are also developed to feed the data to FPGA.
F. Steps for RSA Algorithm Implementation

VHDL MODELING
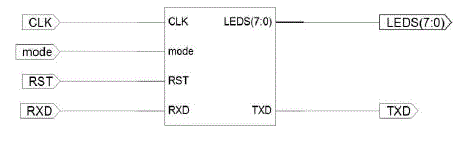
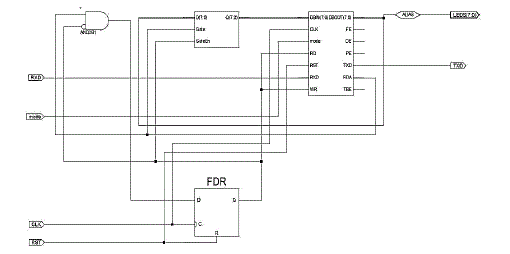
VHDL (VHSIC hardware description language) is a hardware description language used in electronic design automation to describe digital and mixed-signal systems such as field-programmable gate arrays and integrated circuits. This language is fully based on the IEEE 1164 Standards. Here, the whole system is designed with the help of VHDL. The RTL models of this approach are shown in the Fig.3 and 4.
A. Overall RSA RTL model in FPGA
B. UART RTL model in FPGA

SIMULATION, SYNTHESIS AND DISCUSSION
VHDL is commonly used to write text models that describe a logic circuit. Such a model is processed by a synthesis program, only if it is part of the logic design. A simulation program is used to test the logic design using simulation models to represent the logic circuits that interface to the design. This collection of simulation models is commonly called a test bench. VHDL has file input and output capabilities, and can be used as a general-purpose language for text processing, but files are more commonly used by a simulation test bench for stimulus or verification of data. There are some VHDL compilers which build executable binaries. Here, VHDL program is used for RSA, data control, UART and device drivers to write a test bench, to verify the functionality of the design using files on the host computer to define stimuli, to interact with the user, and to compare results with those expected. After the generation of codes that simulates successfully, it may not be synthesized into a real device or is too large to be practical.
So, a step has been taken to design hardware in a VHDL IDE for FPGA implementation using Xilinx ISE to produce the RTL schematic of the desired circuit. After that, the generated schematic can be verified using simulation software which shows the waveforms of inputs and outputs of the circuit after generating the appropriate test bench. Finally, the VHDL model is translated into the gates and wires that are mapped onto a programmable logic device FPGA. Hence it is the actual hardware which is configured as processor chip rather than the VHDL code which is used for implementing the RSA Algorithm.
Once synthesis is over, the input message is in the form of data can be given as input to FPGA from computer via Hyper Terminal or Ethernet in serial communication media. This message is moved to FPGA in binary form with selected bit values one by one. Now, RSA algorithm which is implemented using VHDL program in FPGA processes this message and produces encrypted data as output in the hyper terminal screen. So, the output, which is not in readable format, can be saved in note pad. Now, the encrypted file can be sent for the decryption process to get the original message. All these operations have been carried out in the Spartan 3E FPGA electronic module and its real time output could be seen through hyper terminal screen and not in the form of binary or hex formats. Hence, this FPGA module can be used as a standard device in the secured closed network data communication system.
A. Device Utilization Summary
From device utilization summary, it is clear that total equivalent gates used for the approach is 951 only. And apart from the number of slices, all other components utilized percentile is less than 10 which includes XORs, LUTs and shift registers. Because of total equivalent gate count is very low that results in very low frequency requirement to perform this operation, low power consumption and low cost compared to earlier methods.
B. Simulated Real Time Result
The above figure shows the output of Xilinx Spartan 3E FPGA device. At first the input fed to the FPGA device under normal mode. Then, the same input can be given under encryption mode to get encrypted data. This encrypted data can be saved in note pad to transmit to the receiver side. Now, the encrypted data can be given under decryption mode in the receiver side to get original data.

CONCLUSION
The primary goal of this research project is to develop RSA algorithm on FPGA which can provide a significant level of security as well as can provide a faster processing time. The maximum bit length for both the public and private key is 1024-bit. Beside the security issue, another major concern of this research project is to process the data or file as input.. The VHDL implementation has shown that the language provides a useful tool of practicing the algorithms without drawings of large amounts of logic gates. Although the current key size of this RSA algorithm can provide a sufficient amount of security, a larger key size can always ensure a better security. However, this results in slower processing time.

Figures at a glance
Figure Figure
Figure 1 Figure 2
 

References