Network Topology Based Back/Forward
Sweeping for Load Flow of Radial
Distribution Systems

Soumitri Jena; Abhisek Mishra; Vivek Rastogi

Network Topology Based Back/Forward Sweeping for Load Flow of Radial Distribution Systems

Soumitri Jena¹, Abhisek Mishra², Vivek Rastogi³

P.G Scholar [Power System], Dept. of EE, National Institute of Technology, Hamirpur, India
P.G Scholar [Power System], Dept. of EE, National Institute of Technology, Hamirpur, India
P.G Scholar [Power System], Dept. of EE, National Institute of Technology, Hamirpur, India

Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Abstract

This paper presents a simple network topology based back/forward sweeping method for radial distribution systems. This method uses networktopology based matrices and KCL , KVL based equations. The data are stored in matrix form, then the memory requirement is very less.The current and voltage values have been updated in two subsequent sweeps (Backward and Forward). The requirement of sequential branch numbering has been averted. This method has been tested to IEEE 33 and 69 test systems and time required and accuracy has been found satisfying.

Keywords

Radial distribution system, load flow, Network topology, Back/forward sweep.

INTRODUCTION

Referable to the high R/X ratio and ill conditioned radial structure of distribution systems, conventional methods that has been utilized for load flow of transmission systems fail to converge in distribution network.However modified NR method can be employed for the design, but the size of the Jacobian of a real distribution would be largely sparse for the role.A set of methods has been previously suggested in literature for load flow of the radial distribution network as analysis of distributed systems is very necessary as the connection between power system and consumer.

RELATED WORKS

The conventional methods of load flow presented in[1] and [2] were later found to be very complex and time consuming.Kersting and Mendive[3] and kersting [4] proposed load flow of radial distribution system by using laddernetwork theory but stevens [5] showed that the proposed method become fastest but does not converge in five out of twelve cases it studied.Shirmohammadi [6]presented a new method by using KCL and KVL laws and proposed a new branch numbering scheme, but the memory requirement became very high. Baran and Wu [7] prepared a load flow method by iterating fundamental equations for real, reactive and voltage magnitude. Goswami and Basu[8] proposed a new method but with conditions of no branch is a junction of more than three branches. Daset.al [9] proposed a method of coding at each lateral and sub laterals but with larger systems the coding became more complex.Ghosh and Dash [10] solved load flow equations by considering nodes beyond a node, they have alsoincorporated charging admittances.Aravindhababu [11] has proposed a method based on branch-node power flow (BNPF) but it also added complexity. Ranjanet.al[12] proposed a technique by calculating the voltage at each bus by forward sweeping but it required calculation of real and reactive load at the receiving end node and all branch losses and loads beyond the receiving node.

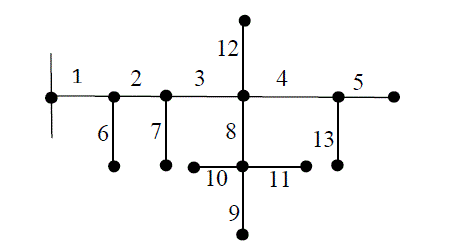
The main objective of this paper is to solve load flow problems for radial systems by using simple KVL and KCL equations with no trigonometric functions used. This method requires a branch and node identification scheme beyond a node, which is required to find out branch current flows and power losses. Based on the topology of the network, the number of laterals (paths) is found out.

Initial voltage of 1p.u across the network assumed and initial power losses in the branches are assumed to be zero.Again, it is assumed that the three phase radial distribution system is balanced and represented by the single line diagram. Charging capacitances are neglected at distribution levels.

METHODOLOGY

The following are steps are to be studied to find out some network based matrices:

Step-1: The system data like branch impedance, load real and reactive power are converted to p.u.

Step-2: Matrix A (Branch-node incidence matrix) is formed by considering branches as rows and nodes as columns, hence the dimensions of the matrix would be (n-1 ×n), where n is the no of nodes of the matrix.

For i th node

Step-3: The number of laterals or the possible paths (ÃÂ¯ÃÂ¿ÃÂ½ÃÂ¯ÃÂ¿ÃÂ½) are found out by calculating the number of end nodes.

Step-4:The next step would be to get the nodes on each lateral. The lateral having maximum number of nodes say (m) is found. Then the matrix say B is supposed to have dimensions of (l ×m).

Step-5:In a radial distribution system, itfinds necessary the branches beyond a branch. Hence a next-linked branch matrix (C) is formed. In the above lateral the number of possible paths is8. Hence the size of C would be13 × 8.However, to reduce memory space up to 4 columnsin this case has to be considered as no branch is connected to more than 3 branches. Here the row number shows the branch number and column denotes the connected branches.

The following steps are then to be considered for load flow calculations:

Step-10: Display Results.

The detailed flow chart of the procedure is shown in APPENDIX.

EXAMPLES

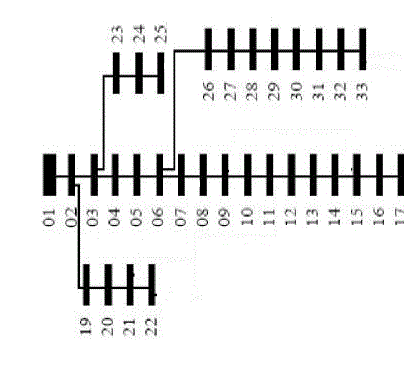
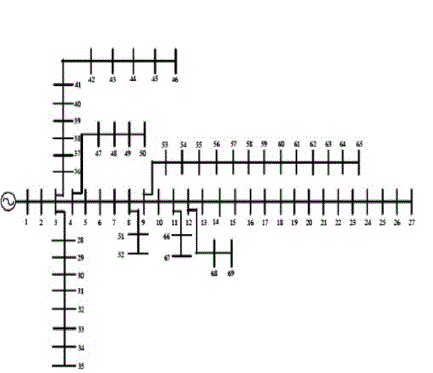
The algorithm is tested on two IEEE test systems. For IEEE 33 bus system data are obtained from [13] and for IEEE 69 bus system data are obtained from [7].Base KV for the systems are 12.66 and base MVA is 100.

For the IEEE 33 bus system total real power load is 3715 KW and total reactive power is 2300 KVAR. Voltage profile across the network is shown in table.1.

Total real power loss is found out to be 202.68 KW and total reactive power loss is 135.14 KVAR.

For IEEE 69 bus system total real power load 3801.9 KW and total reactive power load is 2694.1 KVAR. Voltage profile across the network is shown in table. 2.

Total real power loss is found out to be 224.95 KW and total reactive power loss is 102.15 KVAR.

CONCLUSION

This paper, presents a network topology based load flow for radial distribution system.The data are stored in matrix form, hence the memory requirement is very low.The numbering pattern for the elements is not a concern, for the algorithm. However, the proposed algorithm takes zero initial loss approximation and flat voltage profile across the network. The efficiency of the method tests with satisfying results.

Tables at a glance


Table 1	Table 2

Figures at a glance


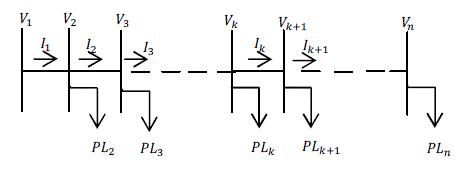Figure 1	Figure 2	Figure 3	Figure 4

References

S.Iwamoto, Y.A.Tamura,“ Load flow calculation method for ill-conditioned power systems,” IEEE Transactions Power Apparatusand Systems,vol. PAS-100, No. 4, pp.1706-1713,1981.

D. Rajicic, Y. Tamura, “ A modification to fast decoupled load flow fornetworks with high R/X ratios,” IEEE Transactionson Power Systems;vol. 3, no.2, pp.743-746,1988.

W.H.Kersting, D.L. Mendive, “ An Application of Ladder Theory to the Solution of Three-Phase Radial Load-Flow Problem,”IEEETransactions on Power Apparatus and Systems; vol. PAS-98 no.7, pp.1060 – 1067, 1976.

W.H.Kersting, “ A Method to Teach the Design and Operation of a Distribution System,” IEEE Transactions on Power Apparatus and Systems;vol. PAS-103, no.7, pp.1945 – 1952, 1984.

R.A. Stevens ,et al., “ Performance of Conventional Power Flow Routines for Real Time Distribution Automation Application,”Proceedings18th Southeastern Symposium on Systems Theory: IEEE Computer Society: 196 – 200, 1986.

D, Shirmohammadi, H.W. Hong, A. Semlyn, G.X. Luo, “ A Compensation Based Power Flow Method for Weakly Meshed Distribution andTransmission Network,” IEEE Transactions on PowerSystems, vol. 3, no.2, pp. 753 762,1988.

M.E. Baran ME and F.F. Wu , “ Optimal Sizing of Capacitors Placed on a Radial Distribution System,” IEEE Transactions on Power Delivery;vol. 4, no. 1, pp. 735 – 743, 1989.

S.K. Goswami and S.K. Basu, “Direct Solutions of Distribution Systems,” IEE Part C (GTD), vol.138, no.1, pp.78 – 88,1991.

D. Das, H.S.Nagi and D.P. Kothari , “Novel Method for solving radial distribution networks,” Proceedings IEE Part C (GTD), vol.141, no.4,pp. 291 – 298, 1991

S. Ghosh and D. Das, “Method for Load-Flow Solution of RadialDistribution Networks,” Proceedings IEE Part C (GTD), vol.146, no.6,pp.641– 648, 1999.

P. Aravindhababu, S. Ganapathy and K.R. Nayar, “ A novel technique for the analysis of radial distribution systems,” International Journal ofElectric Power and Energy Systems, vol. 23, pp. 167–171, 2001.

R. Ranjan and, D. Das , “ Simple and Efficient Computer Algorithm to Solve Radial Distribution Networks,” International Journal ofElectricPower Components and Systems, vol.31, no. 1,: pp.95 -107, 2003.

M.E.Baran and F.F. Wu, “ Network Reconfiguration in Distribution Systems for Loss Reduction and Load Balancing,” IEEE TransactionsonPower Delivery; vol.4, no.2, pp.1401 – 1407, 1989.