Mathematics Department, Foundation Program, Qatar University, P.O Box 2713, Doha, Qatar
Received date: 10/05/16 Accepted date: 24/05/16 Published date: 28/05/16
Visit for more related articles at Research & Reviews: Journal of Statistics and Mathematical Sciences
We establish a functional central limit theorem for the empirical pro-cess of long range dependent stationary multivariate sequences under Gaussian subordination conditions. The proof is based upon a convergence result for cross-products of Hermite polynomials and a multivariate uniform reduction principle, as in Marinucci for bivariate sequences.
Extensive, Inextensive, Bipartite graphs
The problem of faithful extension among infinite chains or linearly ordered sets has been studied in [1,2] and some relevant results have been mentioned in [3]. Moreover, faithful extension between bipartite graphs, alias bivalent tableaux, and faithful extension between posets with constant height have been studied in [4-13]. Here, some theorems of extension and a counter-example of inextensive of finite bipartite graphs are given and a generalization of this example for many bipartite graphs is introduced.
In this section, some important and useful definitions together with notations are used throughout the presented paper.
Definition 1: A simple graph G consist of a non-empty finite set V(G) of elements called vertices and a finite set E(G) of distinct unordered pairs of distinct elements of V(G) called edges. We call V(G) vertex set and E(G) the edge set of G.
Definition 2: If the vertex set of a graph G can be split into two disjoint vertex sets V1 (rank 1) and V2 (rank 2) so that each edge of G joins a vertex of V1 and a vertex of V2, then G is a bipartite graph.
Definition 3: The simple graph G1= (V1, E1) and G2 = (V2, E2) are isomorphic if there is a one-to-one and onto function F from V1 to V2 with the property that a and b are adjacent in G1 if and only if F(a) and F(b) are adjacent in G2, for all a and b in V1. Such a function F is called an isomorphism, [12].
Definition 4: For Two bipartite graphs G and H, G is embedding in H if there exists an isomorphism from G onto restriction of H.
Definition 5: We say that a bipartite graph G extensive if for every bipartite graph H so that G is not embedding in H there exists an extension H* of H by adding a vertex (of rank 1 or 2) and such that G is not embedding in H*. We say that a bipartite graph G inextensive for H if G is not embedding in H but G is mapped into every bipartite H* extension of H by adding a vertex to rank 1or to rank 2.
Definition 6: Two vertices u and v of a graph G are called adjacent if there is an edge {u, v} joining them, and the vertices u and v are then incident with such an edge.
Definition 7: The degree of a vertex v of graph G is the number of edges incident with v.
Definition 8: A vertex of degree 0 is an isolated vertex.
Definition 4 and 5 are found in [14] while definitions 1, 2, 3, 6, 7 and 8 above are found in [12] and for more details, the reader is referred to these references.
For any finite bipartite graph G, call I the set of isolated vertices in G which are incomparable (not adjacent to any one) with all other ones (Throughout this paper we can put this vertices in the vertex set of rank 1 in G). Let G-I be the restriction of G to the complement of I.
The main problem in this part see [14] is that: Does there exist a finite bipartite graphs which is inextensive for infinitely many finite bipartite graphs H considered up to isomorphism or equivalently having unlimited finite cardinals.
Theorem 1: Let G be any bipartite graph without isolated vertices which is incomparable with all the other ones, then G is extensive.
Proof: If G is not embedding in H, it is enough to add a G an isolated vertex.
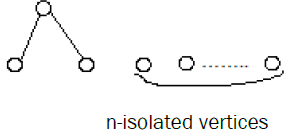
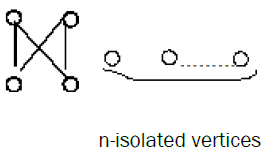
Theorem 2: If G is the graph of the following form with n-isolated vertices, then G is extensive.
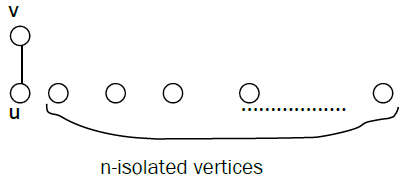
Proof: Let H* be the graph H by adding a vertex μ (in rank 1) which is adjacent to every vertex in rank 2 and not adjacent to all vertices in rank 1. Then u cannot be the image of any isolated vertices in G (if not G it will be not a bipartite graph). Therefore in the image of G there exist a vertex v adjacent to u and of rank 2, but v accept in H a vertex v0 adjacent v and of rank 1, different of the n-isolated vertices, then G is isomorphic to the restriction of H in v0, v; so that G is embedding in H, a contradiction. Therefore G is extensive.
Theorem 3: The bipartite graph G of the following form with one isolated vertex is extensive.
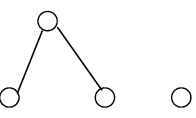
Proof: We have two cases:
Case (i): Either G-I is not embedding in H, then construct H* by adding to H an isolated vertex. Then G-I is not embedding in H*, then G too.
Case (ii): Or G-I is embedding in H but G is not embedding in H. Choose in H a vertex v of rank 2 which is adjacent to at least two vertices of rank 1, after that construct H* by adding a vertex λ which is admit with those in H the same connection as v (with λ not adjacent to v). Suppose that G is embedding in H*. Then there exist an isomorphism F from G to H* and λ belong to F(G). Either v is not belong to F(G): then replace λ by v, there exist an isomorphism from G in H: contradiction. Or v belong to F(G), then neither v nor λ can’t be the top of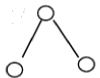 
(and it cannot be two vertices not adjacent to at 
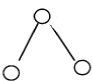): least one of them must be of rank 1 therefore admit in H a vertex of rank 2 adjacent to it: contradiction.
Theorem 4: The bipartite graph G of the following form with one isolated vertex is extensive.
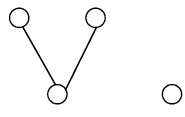
The proof is similar to Theorem 3.
Theorem 5: The following bipartite graph G is extensive
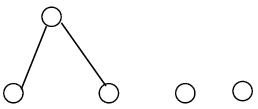
Proof: The same proof stated in Theorem 3 until the case of v belong to F(G); here also neither λ nor v can be the top or foot of the following graph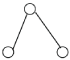 
Necessarily there exists in H et in F(G) a vertex u of rank 2 and two vertices c, d of rank 1 which is adjacent to u, with v and λ every one of them is not adjacent to u, c, d. By hypothesis there exists two vertices a, b of rank 1 which is adjacent to v (of rank 2) and not belong to F(G). These vertices are distinct to c, d and these vertices are not adjacent (one to other) since c and d of rank 1 (on the same set of vertices). Therefore G is embedding in H by the verticesv, a, b, c, d: contradiction.
Theorem 6: The following bipartite graph is extensive.
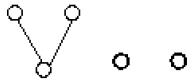
The proof is similar to Theorem 5.
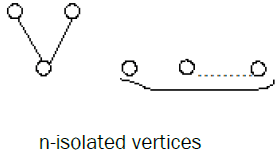
Remark: In general the following bipartite graph with n isolate vertices is extensive.
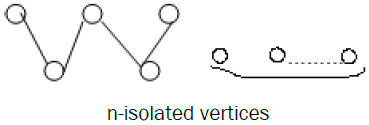
Similarly for the following bipartite graph with n isolated vertices is extensive.
Theorem 7: If any bipartite graph G contains at least one isolated vertex and if G-I nonempty bipartite graph and not admit any vertex of rank 1 adjacent to all the vertices in rank 2, then G is extensive.
Proof: Suppose that G-I is not embedding in H. Then it is enough to define H* by adding an isolated vertex λ. Now suppose that G-I (but not G) is embedding in H. Define the graph H* by adding a vertex λ (of rank 1) adjacent to all the vertices of rank 2 in H. The vertex λ cannot be the image of an isolated vertex in G, because G it will be not a bipartite graph (since the entire vertex in G it will be an isolated vertices). Also λ it will be the image of a vertex in G-I which is adjacent to all vertices of rank 2 in G: contradiction.
Corollary of Theorem 7: The bipartite graph G of the following form with n isolated vertices is extensive.
The proof is similar to Theorem 7.
Theorem 8: If any bipartite graph G contains at least one isolated vertex and if G-I nonempty bipartite graph and not admit any vertex of rank 2 adjacent to all the vertices in rank 1, then G is extensive.
Proof: Suppose that G-I is not embedding in H. Then add an isolated vertex in H.
Now if G-I (but not G) is embedding in H. Define the graph H* by adding a vertex λ (of rank 2) adjacent to all the vertices of rank 1 in H. The vertex λ cannot be the image of an isolated vertex in G, because G it will be not a bipartite graph. Also λ is the image of a vertex in G-I. If λ is the image of a vertex of rank 1 in G-I then all the vertices in the isomorphism of G are isolated vertices or adjacent to λ therefore all it will be of rank 2 in H: therefore G it will be not a bipartite graph: contradiction. Thus λ is the image of a vertex of rank 2 in G-I. Moreover λ is adjacent to all the vertices of rank 1 in G-I; if not a vertex u of rank 1 in G-I and not adjacent to λ it will be of rank 2 in H therefore it will be not adjacent to every vertex of G-I then u belong to I (an isolated vertex): contradiction.
Corollary of Theorem 8: The bipartite graph G of the following form with n isolated vertices is extensive.
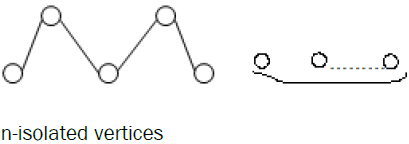
The proof is similar to Theorem 8.
Theorem 9: The bipartite graph G of the following form with one isolated vertex is extensive.
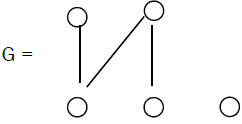
Proof: We have two cases:
Case (i): Either G-I is not embedding in a bipartite graph H, then construct H* by adding to H an isolated vertex. Then G-I is not embedding in H*, then G too.
Case (ii): Or G-I is embedding in bipartite graph H but G is not embedding in H. Choose in H a vertex v of rank 2 which is adjacent to at least two vertices of rank 1, after that construct H* by adding a vertex λ which is admit with those in H the same connection as v (with λ not adjacent to v). Suppose that G is embedding in H*. Then there exist an isomorphism F from G to H* and λ belong to F(G). Either v is not belong to F(G): then replace λ by v, there exist an isomorphism from G in H: contradiction.
Theorem 10: The bipartite graph G with one and only one isolated vertex is extensive.
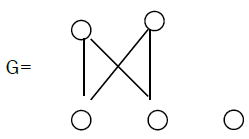
Proof. We have two cases
If G-I is not embedding in H, add an isolated vertex to H.
Now if G-I is embedding in H (but not G), either there exist in H a vertex α which is not belong to any restriction isomorphic to G-I; then add to H a vertex λ which admit the same connections as α (λ is not adjacent to α). Then G is not embedded in H*.
Or there exist a vertex α in H which belong to all the restriction G-I: then add a vertex λ of rank 2 adjacent to α only (if α of rank 1) or add λ in rank 1 adjacent to α only (if α of rank 2) and λ not adjacent to all the other vertices in H in the two cases. Or maybe we are not investigated any precedent cases: then we add a vertex λ of rank 2 adjacent to all the vertices of rank 1. Then G is not embedded in H*.
It will be shown in the following counter-examples that the same bipartite graph in Theorem 9 but with n ≥2 isolated vertices is inextensive.
Counter-example 1: The bipartite graph G with two isolated vertex is inextensive.
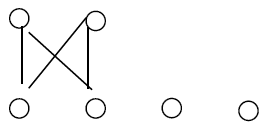
Proof: Construct the graph H of the form
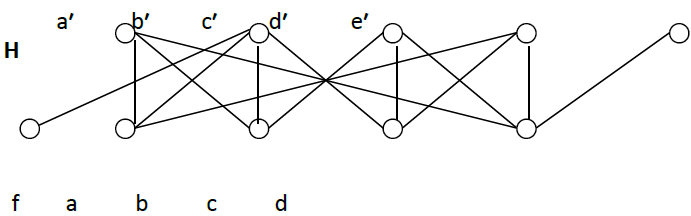
We must firstly verify that the bipartite graph G is not embedding in H, we leave to reader to check it.
Now the proof of G is embedding in H by adding all the (32) possible vertices of rank 1 and 32 possible vertices of rank 2 may be carried out as follows:
If the additional vertex λ is of rank 1 and λ adjacent to d′, e′ whatever its connection with a′, b′, c′ (adjacent or not), then G is embedding in H* by the vertices d′, e′, d, λ, f, b; which is cover eight cases: the case of λ adjacent to d′, e′ (and not adjacent to all the other vertices of rank 2); then s adjacent to a′, d′, e′; then λ adjacent to b′, d′, e′; then λ adjacent to c′, d′, e′; then λ adjacent to a′, b′, d′, e′; then λ adjacent to a′, c′, d′, e′; then λ adjacent to b′, c′, d′, e′; and then λ adjacent to a′, b′, c′, d′, e′.
If λ in rank 1 and λ adjacent to c′, e′ then G is embedding in H* by the vertices c′, e′, d, λ, a, f; which is cover the four new cases: the first case λ adjacent to c′, e′; then λ adjacent to a′, c′, e′; then λ adjacent to b′, c′, e′; and then λ adjacent to a′, b′, c′, e′.
If λ is not adjacent to c′ and d′ then G is embedding in H* by the vertices c′, d′, c, d, λ, f; which is cover new eight other cases: the case of λ not adjacent to a′, b′, c′, d′, e′; then λ adjacent to a′ (and λ not adjacent to the other vertices); then λ adjacent to b′; then λ adjacent to e′; then λ adjacent to a′, b′; then λ adjacent to a′, e′; then λ adjacent to b′, e′; and then λ adjacent to a′, b′, e′.
If λ of rank 1 and λ adjacent to a′, c′ with λ not adjacent to e′ then G is embedding in H* by the vertices a′, c′, λ, b, f, e′; which is cover the four new cases: the first case is λ adjacent to a′, c′; then λ adjacent to a′, b′, c′; then λ adjacent a′, c′, d′; and then λ adjacent to a′, b′, c′, d′.
If λ of rank 1 and λ not adjacent to a′, d′ then G is embedding in H* by the vertices a′, d′, a, d, λ, f; which cover two new cases: the case of λ adjacent to c′ and the case of λ adjacent to b′, c′.
If λ of rank 1 and λ not adjacent to b′, c′, e′ then G is embedding in H* by the vertices b′, c′, b, c, λ, e′; which cover two other cases: the case of λ adjacent to d′ and then λ adjacent to a′, d′.
If λ of rank 1 and λ not adjacent to a′, b′, e′ then G is embedding in H* by the vertices a′, b′, a, b, λ, e′; which cover one other case: the case of λ adjacent to c′, d′.
If λ of rank 1 and λ adjacent to b′, d′ with λ not adjacent to c′, e′ then G is embedding in H* by the vertices b′, d′, λ, a, c′, e′; which cover two other cases: the case of λ adjacent to b′, d′ and then s adjacent to a′, b′, d′.
If λ of rank 1 and λ adjacent to c′, d′ with λ not adjacent to e′ then G is embedding in H* by the vertices c′, d′, λ, c, f, e′; which cover the thirty-two and last case: the case of λ adjacent to b′, c′, d′.
The reader is going to complete the proof when the additional vertex will be of rank 2.
Counter example 2: The bipartite graph G with three isolated vertex is inextensive.
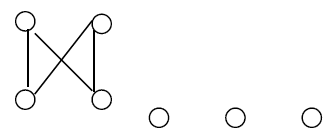
Proof: Construct the graph H of the form
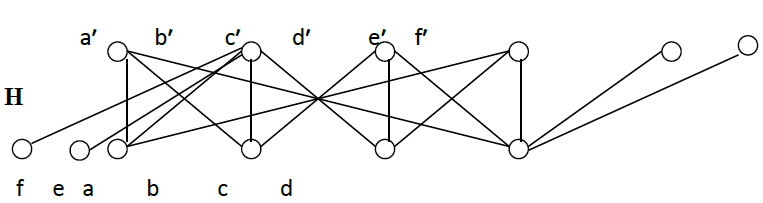
It should be verified that G is not embedding in H.
The proof is similar to counter-example 1.
Before we give a generalized counter example, we find that the same bipartite graph G in counter example 2 is inextensive by another bipartite graph S with same cardinal of vertices ( n = 12) as H but different construction as we see in the following:
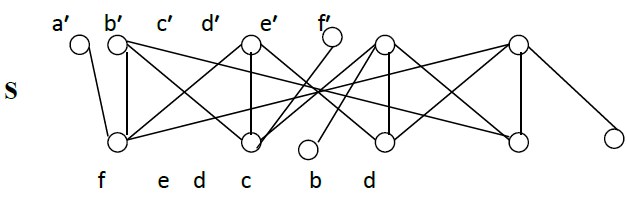
The proof is similar to counter-example 1
At the end of this paper we give a generalization of the following counter example for the same bipartite graph in with I = n (n ≥ 2), which is inextensive.
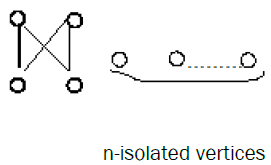
Generalized counter example: The bipartite graph G of the following form with I = n (n ≥ 2) is inextensive.
Proof. Construct the same bipartite graph H in counter example 2 but we add (n-1) vertices of rank 2 adjacent to d only and we add (n-1) vertices in rank 1 adjacent to b′ only.
It should be verified that G is not embedding in H.
The proof is similar to the counter example 1.
The extensiveness of bipartite graphs has been studied, an example of in extensive of bipartite graph has been given and an in extensive general theorem for bipartite graphs has been proved. We can conclude that there is an inextensivness for bipartite graphs and also there is more than one bipartite graph H for which the bipartite graph G in counter example 2 is in extensive. In our opinion there is an open problem concerning the inextensiveness of bipartite graphs should be solved by finding another bipartite graphs which are inextensive.
This publication was made possible because of the support of Qatar University. Its content are solely the responsibility of the author and do not necessarily represent the official views of the Qatar University
Menu