Noise Reduction of Vibration Signals in
Rotary Machines using Neighbourhood Correlation of Wavelet Transform Coefficients

Shweta Garde; Preety D Swami

Noise Reduction of Vibration Signals in Rotary Machines using Neighbourhood Correlation of Wavelet Transform Coefficients

Shweta Garde¹, Preety D Swami ²

Department of Electronics & Communication , Samrat Ashok Technological Institute, Vidisha, India
Department of Electronics & Instrumentation, Samrat Ashok Technological Institute, Vidisha, India

Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Abstract

Faulty gears and bearings are a major source of problem in rotating machines. These faults appear as impulses at periodic intervals resulting in form of characteristic frequency of the machinery. To retrieve the characteristic fault frequencies of the vibration signal, denoising of signal is an essential preprocessing step. This paper presents two robust techniques for denoising of vibration signals corrupted by Additive White Gaussian Noise. The proposed method uses the Stationary Wavelet Transform (SWT) and the Dual Tree Complex Wavelet Transform (DTCWT). The proposed methods are very efficient due to their shift invariance property and have reduced aliasing effect than other methods such as Discrete Wavelet Transform(DWT), Continuous Wavelet Transform(CWT), Short Time Fourier Transform(STFT) etc. For reduction of noise, owing to the fact that neighbouring wavelet coefficients belonging to signal are correlated, the thresholding of noisy wavelet coefficients is done by selecting a window and comparing the averaged noisy wavelet coefficients inside the window with a threshold. Denoising results are compared by varying the window size and the best window length is chosen for denoising. Experiments are carried out on simulated vibration signals as well as on real time signals. The comparison of the results of the proposed methods using DTCWT and SWT for synthetic signal is done using the signal to noise ratio(SNR). For comparison of results of the real time signal, another statistical parameter Kurtosis is chosen.

Keywords

SWT, DWT, DTCWT, Thresholding, Minimaxi

INTRODUCTION

In this modern world machines play crucial role in manufacturing industries. These machines reduce man power and time consumption hence these machines are helpful in industrial revolution. Different types of machines are used in industries which contain rotating parts such as bearings, gears, rotors etc. Due to various reasons such as mechanical vibrations, stresses, inadequate lubricant and asymmetric loading, breakdown happens and different types of faults take place in machines. These faults lead to slow or total stoppage in production and therefore economical loss and safety problems are faced by industries.

To overcome these problems, some efficient and fast techniques are required that are able to not only detect faults, but also remove noise from the faulty signals. These vibration signals contain useful information to detect the faults [1-2].

For the past few years, large amount of work is being done in this field to detect faults and for this many techniques are used such as the Fourier Transform (FT) [3] and the Short Time Fourier Transform (STFT) [4]. Fourier Transform gives the complete information about the frequency content of the signal but the time information is missing. STFT gives the information about both time and frequency of the signal, but the selection of window size is a big concern. Wavelet transform has now become popular that gives perfect time and frequency information of a signal under investigation. Wavelet transform can be basically categorized into Continuous Wavelet Transform (CWT) [5] and Discrete Wavelet Transform (DWT) [6-8]. Main advantage of DWT over CWT is that it is comparatively faster, easier to implement and avoids redundancy. However DWT has some drawbacks such as lack of shift invariance and aliasing effect. To overcome these problems, in this paper, two techniques for denoising of vibration signals are proposed that use DTCWT [9] and SWT [10].

The paper organization is as follows: A short description of DTCWT and SWT is given in Section II that describes the functioning of the transforms and their supremacy to the previous transforms. Section III presents the proposed denoising algorithm. In Section IV, comparisons of results and their analysis is done. Finally conclusions are given in Section V.

DTCWT AND SWT

A. DTCWT

DTCWT stands for ‘Dual Tree Complex Wavelet Transform’. As the name indicates, it contains two dual tree wavelet basis functions and due to this property the problem of lack of shift invariance, coefficient oscillation and aliasing effect do not occur [11]. It is very powerful and efficient transform for multiple fault detection and noise reduction. In this transform, two parallel DWTs with different lowpass-highpass filters are used for decomposition and reconstruction of signal and hence it is highly directionally selective. For ψg(t) and ψh(t) denoting two real valued wavelets used for lowpass and highpass filters respectively, the complex wavelet ψc(t) is given by

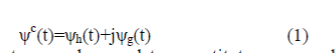Thus two real wavelets constitute a complex analytical wavelet which is supported on positive frequency axis.

B. SWT

SWT represents ‘Stationary Wavelet Transform’. SWT is also an efficient transform as it is an inherently redundant scheme [10]. The output of each level of SWT contains the same number of samples as the input. Thus for decomposition of N levels, there is a redundancy of N in wavelet coefficients. This makes it a shift invariant transform that is not achieved by DWT. In SWT, shift invariance is achieved by removing the downsamplers and upsamplers in the DWT and upsampling the filter coefficient by a factor of 2(j-1) in the jth level of algorithm.

PROPOSED WORK

Overlapping of unwanted, out of band frequencies with desired frequencies of signal, causes distorted spectrum of signal and is termed as Aliasing effect. These types of signals cannot be filtered properly and create serious impacts in many practical applications. DWT avoids aliasing, only if the wavelet and scaling coefficients are not changed. However during filtering, thresholding or any other coefficient processing step, these coefficients change and aliasing is introduced in the signal. SWT and DTCWT have no such limitation and thus give alias free spectrum of the signal. This can be well understood from the following sub-section.

A. Decomposition of multiple harmonic signal

The aliasing of signals caused by DWT is demonstrated by generating a synthetic signal S1(t) having multiple harmonics, at a sampling frequency 2000Hz, given by

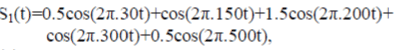Where, t ÃÂÃâ [0,0.256]. From the equation of this signal, it is clear that five frequencies are present in the signal, that are 30, 150, 200, 300 and 500Hz. Decomposition of this signal via DWT, DTCWT and SWT is shown in Fig. 1(a), Fig. 1(b) and Fig. 1(c) respectively. The frequency contents of the decomposed signals are obtained by computing their FFT. The FFTs of decomposed subbands are plotted in Fig. 1(d), Fig. 1(e) and Fig. 1(f) for DWT, DTCWT & SWT respectively.

From the spectrum of subbands, DWT shows distorted frequency spectrum (Fig. 1(d)), in which unwanted frequency component such as 800 and 1000Hz are visible in d3, d2 and in d1 subbands, whereas these frequencies are not present in the signal. On the other hand, spectrums of DTCWT (Fig. 1(e)) and SWT (Fig. 1(f)) show actual frequencies 30,150 and 500Hz in a1, d1 and d4 subbands respectively and d2 and d3 subbands both show 200 and 300Hz frequencies. For both DWT and SWT same wavelet (db8) is used for the decomposition of the signal. Thus it is clear that SWT and DTCWT do not suffer from the problem of aliasing. Also in DWT, the shape of lowest approximation coefficients is not as clear as in SWT and in DTCWT.

B. Proposed denoising method

For denoising of signal in the proposed work, the concept of thresholding of averaging of noisy wavelet coefficients inside a window is used with both SWT and DTCWT. This is done due to the fact that the wavelet coefficients belonging to signal class are correlated with their neighbors, while wavelet coefficients belonging to noise are not. Thus first of all, the signal is decomposed using SWT and DTCWT which results in separate approximation and detail coefficients for each level of decomposition. The threshold value is selected using ‘Minimaxi’ method and is level adaptive, that is, for each level a different threshold is selected. Instead of comparing a single wavelet coefficient with the threshold, the average of noisy wavelet coefficients inside a window is compared with the threshold and the centre wavelet coefficient is replaced by the thresholded value. This procedure will be repeated for every subband.

As shown in Fig. 2, for a window of size 3, the coefficient Wi will be thresholded if (Wi-1+Wi+Wi+1)/3 is greater than the selected threshold.

The inverse wavelet transform of thresholded coefficients provide the denoised signal.

EXPERIMENTS AND RESULTS

A. Denoising of simulated faulty signal

Faulty bearings can be seen as a series of impulses. Moreover, noise is always present when these signals are captured with the help of accelerometers. In this subsection, a faulty signal is simulated and noisy signals are generated by adding Additive White Gaussian Noise of various standard deviations. The proposed method applies level adaptive threshold to the average of coefficients of the noisy synthetic signal inside a window of a particular subband. The procedure is repeated for every subband with a different level adaptive threshold. The simulated signal is represented by

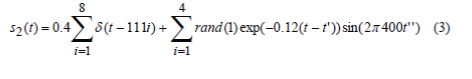Here, t ÃÂÃâ [0, 1023] is the no. of samples, t’ shows a delay of 204.8 seconds and t’’ ÃÂÃâ [0, 0.5120-1/Fs, where 1024/Fs=0.5120]. The sampling frequency (Fs) of signal is 2000Hz.

For experimentation, noisy signals are generated by adding noise levels of 0.01, 0.02, 0.03, 0.04 & 0.05 standard deviation. The noisy signals are denoised by applying the proposed averaging and thresholding method on the DTCWT as well as SWT coefficients. The denoising results, by varying the window length to 3, 5 & 7 are given in Table 1 for DTCWT and in Table II for SWT.

Fig 3(a), 3(b), 3(c) & 3(d) shows the noise free simulated faulty signal, noisy simulated faulty signal (for the noise of 0.02 standard deviation) and denoised signals by DTCWT and SWT respectively.

From Table 1, it can be observed that DTCWT gives the best denoising results for a window size of 3 for all levels of noise standard deviations. From Table II, it can be observed that SWT gives best denoising results for window size 5 most of the times, for all levels of noise standard deviations. Moreover a comparison of DTCWT & SWT denoising shows much improved results of SWT denoising as compared to DTCWT denoising for all window size.

B. Denoising of real time faulty signal

The proposed denoising algorithm is also tested on real time faulty signal. The real time faulty signal is taken from CWRU bearing data Center [12]. Reliance electric motor with torque transducer, dynamometer and control electronics constitutes the test setup.

This signal contains fault in inner race at fan end side. The sampling frequency of the signal is 12000Hz. Diameter of inner race is .007 inches and load is 1 HP. For this signal input SNR is not known, thus for the comparison of results, statistical parameter known as kurtosis [13], [14] is calculated, and is given by the equation

Here μ and σ are mean and standard deviation of signal(x). The denoising results are shown in Fig.4. The kurtosis for noisy signal is 5.8444. Using averaging techniques for window size 7 and soft thresholding with SWT, kurtosis for denoised signal is 31.3923 whereas for DTCWT it is 28.6920. This shows better performance of SWT over DTCWT.

From Fig.4 it can be observed that using SWT, seven impulses are visible in Fig.(4(c)). Whereas, for same window size DTCWT gives six impulses, one impulse is lightly suppressed in Fig.(4(b)). Thus SWT in comparison to DTCWT not only suppresses noise to a greater extent but also retains the characteristic impulses.

CONCLUSION

This paper presents a new and efficient technique of denoising of noisy vibration signals. In the proposed work, DTCWT and SWT are used instead of DWT as they are shift invariant and do not introduce aliasing. The noisy vibration signal is decomposed into subbands and at each subband coefficients are thresholded according to its average value with its neighbors inside a window. From the analysis of experiments and results, it is diagnosed that SWT gives better results than DTCWT for same window size. Also SWT is easily implemented and is fast, which is a basic need of today for practical applications whereas DTCWT contains complexity due to two wavelet basis functions instead of single wavelet basis function. Further, SWT effectively suppresses the noise and at the same time retains the characteristic frequency of the vibration signal.

Future work proposes testing of the algorithm for different load values and for various gears and rotary parts. Also improved results are expected by considering not only the neighboring wavelet coefficients, but also parent and child coefficients’ relationship.

Tables at a glance


Table 1	Table 2

Figures at a glance


Figure 1	Figure 2	Figure 3	Figure 4

References

G. Dalpiaz, A. Rivola, and R. Rubini, “Effectiveness and sensitivity of vibration processing techniques for localfault detection in gears,” Mechanical Systems and Signal Processing, vol. 14, no. 3, pp. 387-412, May 2000.

C. M. Harris, and A. G. Piersol, Harris shock and vibration handbook, 5th ed., Mcgraw-Hill, 2002.

H. Mahgoun, R. E. Bekka, and A. Felkaoui, “Gearbox fault detection using a new denoising method based on ensemble emphirical mode decomposition and FFT,” Mechanical Systems and Signal Processing, vol. 11, no. 3, pp. 331-350,

W. J. Staszewski, and G. R. Tomlinson, “ Local tooth fault detection in gear boxes using a moving window procedure,” Mechanical Systems and Signal Processing, vol. 11, no.3, pp.331-350, May 1997.

R. M. Rao, and A. S. Bopardikar, Wavelet Transforms: Introduction to theory and applications, 6th ed., Pearson Education, 2005.

R. polikar “The wavelet tutorial by RobiPolikar,” Available: http://users.rowan.edu/~polikar/WAVELETS/WTtutorial.html, 1996.

R. Rubini, and U. Meneghetti, “Application of the envelope and wavelet transform analysis for the diagnosis of incipient faults in ball bearings,” Mechanical Systems and Signal Processing, vol. 15 no. 2, pp. 287-302, March 2001.

J. Antonino-Daviu, A. Riera-Guasp, J. Roger-Folch, F. Martinez-Gimenez, and A. Peris, “ Application and optimization of the discrete wavelet transform for the detection of broken rotor bars in induction machines,’’ Applied and Computational Harmonic Analysis, vol. 21 , no.2, p

Y. Wang, Z. He, and Y. Zi , “Enhancement of signal denoising and multiple fault signatures detecting in rotating machinery using dual-tree complex wavelet transform,” Mechanical Systems and Signal Processing, vol. 24, no. 1, pp.119-137, Jan. 2010.

D. L. Fugal, Conceptual Wavelets in Digital Signal Processing, Space & Signal Technologies LLC, 2009.

I. W. Selesnick, R. G. Baraniuk, and N. G. Kingsbury “The dual tree complex wvelet transform”. IEEE signal processing magazine, vol. 22, no. 6, pp. 123-151, Nov. 2005.

Bearing data center, www.eecs.case.edu/laboratory/bearing.

J. Antoni, “The spectral kurtosis: a useful tool for characterising non-stationary signals,” Mechanical Systems and Signal Processing, vol. 20, no. 2, pp. 282–307, Feb. 2006 .

J. Antoni, and R.B. Randall, “The spectral kurtosis: application to the vibratory surveillance and diagnostics of rotating machines,” Mechanical Systems and Signal Processing, vol. 20, no. 2, pp. 308–331, Feb. 2006. detection of broken rotor bars in induction machines,’’ Applied and Computational Harmonic Analysis, vol. 21 , no.2, pp. 268–279, Sep. 2006.