Keywords
|
| Baseline Wander, Electrocardiographic, Noise Reduction, Adaptive Filter, LMS Algorithm |
INTRODUCTION
|
| Baseline wander and power line interference reduction is the first step in all electrocardiograph (ECG) signal processing. The baseline wander is caused by varying electrode-skin impedance, patient’s movements and breath. This kind of disturbances is especially present in exercise electrocardiography, as well as during ambulatory and Holter monitoring. The ECG signal is also corrupted by additive 50 or 60 Hz power line (AC) interference. This kind of disturbance can be modelled by a sinusoid with respective frequency and random phase. These two artifacts are the dominant artifacts and strongly affect the ST segment, degrade the signal quality, frequency resolution, produces large amplitude signals in ECG that can resemble PQRST waveforms and masks tiny features that are important for clinical monitoring and diagnosis. |
| The widely used least-mean-square (LMS) algorithm has been successfully applied to many filtering applications , including signal modelling, equalization, control, echo cancellation, biomedicine, or beam forming. The correlation between the additive noise that corrupts the clean signal (primary signal) and the random noise in the reference input (adaptive filter input) is necessary to adaptively cancel the noise of the primary signal. The adjustable weights are typically determined by the LMS algorithm because of its simplicity and low computational complexity. |
| Adaptive filter is a primary method to filter ECG signal, because it does not need the signal statistical characteristics. This paper presents a novel adaptive filter for removing the artifacts from ECG signals based of Constrained Stability Least Mean Square (CSLMS) algorithm. This algorithm is derived based on the minimization of the squared Euclidean norm of the difference weight vector under a stability constraint defined over the posterior estimation error. The adaptive filter essentially minimizes the mean-squared error between a primary input, which is the noisy ECG, and a reference input, which is either noise that is correlated in some way with the noise in the primary input or a signal that is correlated only with ECG in the primary input. Different filter structures are presented to eliminate the diverse forms of noise. Finally, this algorithm is applied on ECG signals from the MIT-BIH data base and compared its performance with the conventional LMS algorithm. The results show that the performance of the CSLMS based algorithm is superior to that of the LMS based algorithm in noise reduction. |
DRAWBACKS OF EXISTING WORK
|
| Adaptive filtering techniques are used in existing system. One method is LMS (Least Mean Square) based adaptive recurrent filter to acquire the impulse response of normal QRS complexes. The main processes of LMS algorithm are filtering process and adaptation process and another method is Normalized LMS (NLMS) algorithm with decreasing step size. Normalized LMS (NLMS) algorithm is another class of adaptive algorithm used to train the coefficients of the adaptive filter. This algorithm takes into account variation in the signal level at the filter output and selecting the normalized step size parameter that results in a stable as well as fast converging algorithm. A common major drawback of adaptive noise canceller based on LMS and NLMS algorithms is the large value of excess mean-square error which results in signal distortion n the noise-cancelled signal. |
OBJECTIVE OF PROPOSED WORK
|
| ECG signal processing in an embedded platform is a challenge which has to deal with several issues. One of the commonest problems in ECG signal processing is baseline wander removal and noise suppression, which determines posterior signal process. In this paper, two filtering techniques are presented and implemented to our knowledge. A novel adaptive noise reduction system is used to suppress power line interference (PLI) and baseline wander (BW) noise in electrocardiographic (ECG) signals. |
| The proposed system is a novel adaptation for filtering Cardiac signals in continuous stationary and non-stationary environments in biotelemetry systems, which are characterized by sudden changes of the signal statistics due to physiological, non-physiological reasons and noises due to free space propagation. The considered CSLMS algorithm is based on the concept of difference quantities and the constraint of equilibrium in the sequence of a posteriori estimation errors. |
A. ECG SIGNAL PROCESSING
|
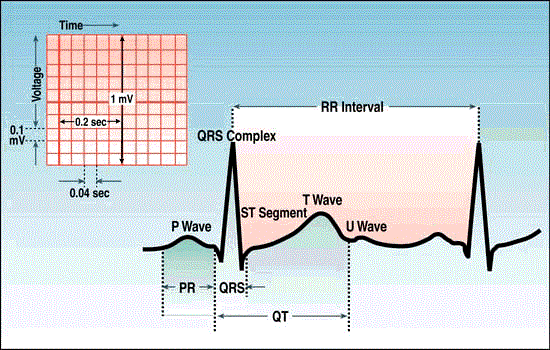
| The electrocardiographic (ECG) signal is the electrical representation of the hearts activity. Computerized ECG analysis is widely used as a reliable technique for the diagnosis of cardiovascular diseases. |
| The figure.1 shows representation of ECG signal is the most commonly used biomedical signal in clinical practice. However, ambulatory ECG recordings obtained by placing electrodes on the subject’s chest are inevitably contaminated by several different types of artifacts. Commonly encountered artifacts include baseline wander, powerline interference, physiological signals generated by other organs of the body or induced by muscular contractions related to breathing, and high-frequency random noise. Baselines wander and power line interference reduction is the first step in all electrocardiographic (ECG) signal processing. |
B.ECG PREPROCESSING
|
| Common to all types of ECG analysis whether it concerns resting ECG interpretation, stress testing, ambulatory monitoring, or intensive care monitoring is a basic set of algorithms that condition the signal with respect to different types of noise and artifacts, detect heartbeats, extract basic ECG measurements of wave amplitudes and durations, and compress the data for efficient storage or transmission. Some algorithms are frequently implemented to operate in sequential order, information on the occurrence time of a heartbeat, as produced by the QRS detector, is sometimes incorporated into the other algorithms to improve performance. The complexity of each algorithm varies from application to application so that, for example, noise filtering performed in ambulatory monitoring is much more sophisticated than that required in resting ECG analysis. |
| In the preprocessing techniques of initial step is noise removal technique , there are three types of noise represented in ECG signal analysis like EMG noise that is random noise, power line nose and composite noise. Random noise is basically maximum EMG noise level was the scaling of random sequence and the multiplication to Vpp with reduced ratio of 1/8. Power line interference was modeled by 50 Hz sinusoidal function with multiplication on amplitude. The maximum 50 Hz noise level was the scaling of random sequence and the multiplication to Vpp with reduced ratio of ¼. Composite noise is represented by combination of the noise adding functions. The next step for the preprocessing technique is the filtering techniques which is primarily used for preprocessing of the signal and have as such been implemented in a wide variety of systems for ECG analysis. |
C.BASE LINE WANDER
|
| Removal of baseline wander is required in order to minimize changes in beat morphology that do not have cardiac origin, which is especially important when subtle changes in the ‘‘low-frequency’’ ST segment are analysed for the diagnosis of ischemia, which may be observed, for example, during the course of a stress test. The frequency content of baseline wander is usually in the range below 0.5 Hz; however, increased movement of the body during the latter stages of a stress test further increases the frequency content of baseline wander. Patients unable to perform a traditional treadmill or ergo meter stress test may still be able to perform a stress test by sitting, running an ergo meter by hand, or using a special rowing device. In such cases, baseline wander related to motion of the arms severely distorts the ECG signal. |
| During bradycardia, the heart rate may drop approximately 40 beats/minute, implying that the lowest frequency contained in the ECG is approximately 0.67 Hz. As the heart rate is not perfectly regular but always fluctuates from one beat to the next, it is necessary to choose a slightly lower cut-off frequency such as 0.5 Hz. If too high a cut-off frequency is employed, the output of the high pass filter contains an unwanted, oscillatory component that is strongly correlated to the heart rate. |
| In certain situations, baseline wander becomes particularly pronounced at higher heart rates such as during the latter stages of a stress test when the workload increases. Then, it may be advantageous to couple the cut-off frequency to the prevailing heart rate, rather than to the lowest possible heart rate, to further improve baseline removal. Linear filtering with time-variable cut-off frequency was initially suggested for offline processing of ECG signals. |
D.POWER LINE INTERFERENCE
|
| Electromagnetic fields caused by a power line represent a common noise source in the ECG that is characterized by 50 or 60 Hz sinusoidal interference, possibly accompanied by a number of harmonics. Such narrowband noise renders the analysis and interpretation of the ECG more difficult, as the delineation of low-amplitude waveforms becomes unreliable and spurious waveforms may be introduced. Although various precautions can be taken to reduce the effect of power line interference, for example, by selecting a recording location with few surrounding electrical devices or by appropriately shielding and grounding the location, it may still be necessary to perform signal processing to remove such interference. |
ADAPTIVE FILTER ALGORITHMS
|
| Adaptive filters are self-designing filters based on an algorithm which allows the filter to learn the initial input statistics and to track them if they are time varying. These filters estimate the deterministic signal and remove the noise uncorrelated with the deterministic signal. Adaptive filters are self-designing using a recursive algorithm. It is useful if complete knowledge of environment is not available a priori. |
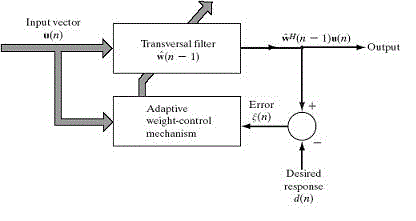
| In the figure.2 shows Adaptive Filter Structure for Obtained signal u (n) from sensor contains not only desired signal d (n) but also undesired noise signal ξ (n). Therefore measured signal from sensor is distorted by noise ξ (n). At that time, if undesired noise signal ξ (n) is known, desired signal d (n) can be obtained by subtracting noise signal ξ (n) from corrupted signal u (n). However entire noise source is difficult to obtain, estimated noise signal ξ’ (n) is used. |
| The estimate noise signal ξ’ (n) is calculated through some filters and measurable noise source x (n) which is linearly related with noise signal ξ (n). After that, using estimated signal ξ’ (n) and obtained signal u (n), estimated desired signal d’ (n) can be obtained. If estimated noise signal ξ’ (n) is more close to real noise signal ξ(n), then more desired signal is obtained. In the active noise cancellation theory, adaptive filter is used. Adaptive filter is classified into two parts, adaptive algorithm and digital filter. Function of adaptive algorithm is making proper filter coefficient. General digital filters use fixed coefficients, but adaptive filter change filter coefficients in consideration of input signal, environment, and output signal characteristics. |
A.CONVENTIONAL LMS ALGORITHM
|
| Consider a length L, LMS based adaptive filter, which takes an input sequence x (n) and updates the weights as |
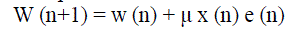 (1) (1) |
| In equation (1), w(n) = [ w0(n) w1(n) . . . wL-1(n)]t is the tap weight vector at the nth index, x(n) = [ x(n) x(n-1). . . x(n-L+1) ], e(n) = d(n) – wt(n)x(n), with d(n) = s1(n)+ p1(n), being so-called the desired response available during initial training period and μ denoting so-called step-size parameter. |
| In order to remove the noise from the ECG signal, the ECG signal S1 (n) corrupted with noise signal P1 (n) is applied as the desired response d1 (n) to the adaptive filter shown in Figure 2.1. If the noise signal P2(n), possibly recorded from another generator of noise that is correlated in some way with P1(n) is applied at the input of the filter, i.e., x(n) = P2(n) the filter error becomes e(n) =[ S1(n) + P1(n) ] – y(n). Where, y(n) is the filter output and it is given by, |
 (2) (2) |
| In equation (2), since the signal and noise are uncorrelated, the mean square error (MSE) becomes |
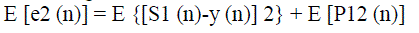 (3) (3) |
| Minimizing the MSE results in a filter output which is the best least-squares estimate of the signal S1 (n). |
B. NORMALIZED LMS (NLMS) ALGORITHM
|
| Normalized LMS (NLMS) algorithm is another class of adaptive algorithm used to train the coefficients of the adaptive filter. This algorithm takes into account variation in the signal level at the filter output and selecting the normalized step size parameter that results in a stable as well as fast converging algorithm. The weight update relation for NLMS algorithm is as follows, |
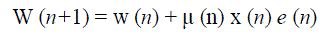 |
| The variable step can be written as, |
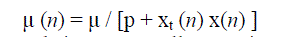 |
| The parameter p is set to avoid denominator being too small, step size parameter too big and to prevent numerical instabilities in case of a vanishingly small squared norm. Here μ is fixed convergence factor to control maladjustment. A common major drawback of adaptive noise canceller based on LMS and NLMS algorithms is the large value of excess mean-square error which results in signal distortion in the noise-cancelled signal. |
C.CONSTRAINED STABILITY LMS (CSLMS) ALGORITHM
|
| The proposed system is a novel adaptation for filtering Cardiac signals in continuous stationary and non-stationary environments in biotelemetry systems, which are characterized by sudden changes of the signal statistics due to physiological, non-physiological reasons and noises due to free space propagation. The considered CSLMS algorithm is based on the concept of difference quantities and the constraint of equilibrium in the sequence of posterior estimation errors. |
| The weight update relation for CSLMS algorithm is as follows, |
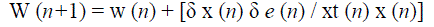 |
| Where δx (n) = x (n) - x (n - 1) is the difference between two consecutive input vectors. Also δe (n) = e (n) - e (n - 1) is the difference in the a priori error sequence. The weight adaptation rule can be made more robust by introducing a small positive constant “p” into the denominator to prevent numerical instabilities in case of a vanishingly small squared norm and by multiplying the weight increment by a constant step size μ to control the speed of the adaptation. Now the weight update equation for CSLMS algorithm can be written as, |
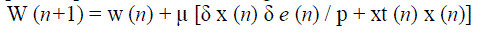 |
| In the CSLMS algorithm the time-varying step-size that is inversely proportional to the squared norm of the difference between two consecutive input vectors rather than the input data vector as in the NLMS. This algorithm provides significant improvements in decreasing mean-squared error (EMSE) and consequently minimizing signal distortion |
PROBLEM DEFINITION
|
| Baselines wander and power line interference reduction is the first step in all electrocardiographic (ECG) signal processing. The baseline wander is caused by varying electrode-skin impedance, patients’ movements and breath. The ECG signal is also degraded by additive 50 or 60 Hz power line (AC) interference. Adaptive filter is a primary method to filter ECG signal, because it does not need the signal statistical characteristics. Here presents a novel adaptive filter for removing the artifacts from ECG signals based on Constrained Stability Least Mean Square (CSLMS) algorithm. The considered CSLMS algorithm is based on the concept of difference quantities and the constraint of equilibrium in the sequence of posterior estimation errors. The method, which applies nonlinearities to the error and input signal sequences, which can be derived using the Lagrange multiplier method as a generalization of the normalized LMS algorithm. |
| The overall System implementation is shown in Figure.3 for simulated ECG segment with designed noises was used to examine filter output. Noises contained EMG, 50 Hz power line and baseline wanders. Low pass filter, High pass filter and Band pass filters are designed with FIR filter, Conventional LMS adaptive Filter, Normalized LMS adaptive Filter (NLMS) and Constrained Stability LMS adaptive Filter (CS LMS). The filtering performance is compared.. The detailed description is given in the following sub-section. |
| The system uses the benchmark MIT-BIH arrhythmia database ECG recordings as the reference for our work and real noise is obtained from MIT-BIH Normal Sinus Rhythm Database (NSTDB). In this simulations we consider both stationary (PLI) and non-stationary (BW) noises. |
| In this paper, first collected 4000 samples of the pure ECG signal from the MIT-BIH arrhythmia database(data105) and it is corrupted with real baseline wander (BW) taken from the MIT-BIH Noise Stress Test Database. The contaminated ECG signal is applied as primary input to the adaptive filter. The real BW is given as reference signal. Different filter structures were implemented using the LMS, NLMS and CSLMS algorithms to study the relative performance and results are plotted. |
RESULTS AND DISCUSSION
|
| The proposed method has been validated using several ECG recordings with a wide variety of wave morphologies from MIT-BIH arrhythmia database. Here used the benchmark MIT-BIH arrhythmia database ECG recordings as the reference for simulation work and real noise is obtained from MIT-BIH Normal Sinus Rhythm Database (NSTDB). In simulations, consider both stationary (PLI) and non-stationary (BW) noises. |
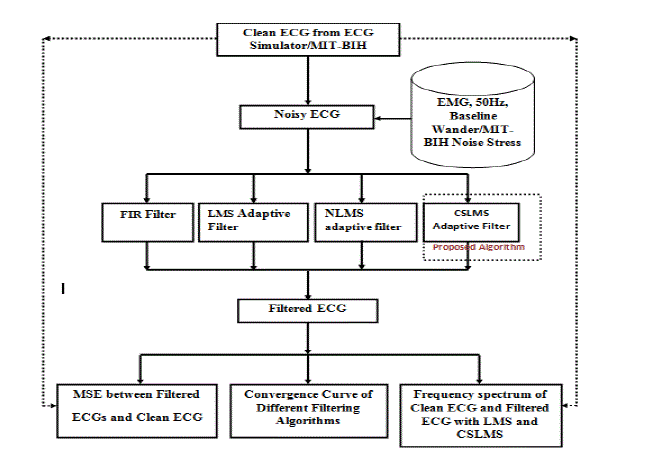
| The figure.4 and 5 shows frequency spectrum of signal with base line wander after LMS filtering algorithm, which is represented arrhythmia data base consists of 48 half hour excerpts of two channel ambulatory ECG recordings, which were obtained from 47 subjects, including 25 men aged 32-89 years, and women aged 23-89 years. The recordings were digitized at 360 samples per second per channel with two bit resolution data set of five records (records 101, 102, 103, 104 and 105). |
| Evaluated the performance of the Algorithm in terms of Minimum MSE (MMSE), MSE, and Excess MSE (EMSE) based on the above discussions we have concluded in two problems, which is in terms of Baseline wander reduction and adaptive power noise reduction |
A.BASELINE WANDER REDUCTION
|
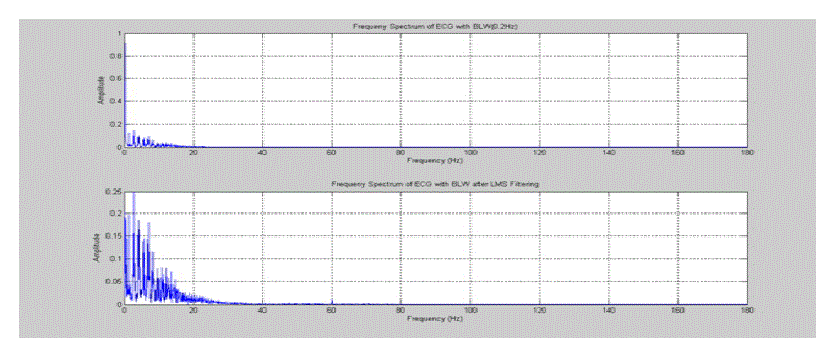
| In this work, first collected the pure ECG signal from the MIT-BIH arrhythmia Database(dataI05) and it is corrupted with real baseline wander (BW) taken from the MIT-BIH Noise Stress Test Database (NSTDB).The contaminated ECG signal is applied as primary input to the adaptive filter. The real BW is given as reference signal. Different filter structures were implemented using the LMS and CSLMS algorithms to study the relative performance and results are plotted in figure.6 for average LMS algorithm gets SNR improvement 7.4648dB, where as CSLMS gets 7.7115dB. |
B.ADAPTIVE POWER-LINE NOISE REDUCTION
|
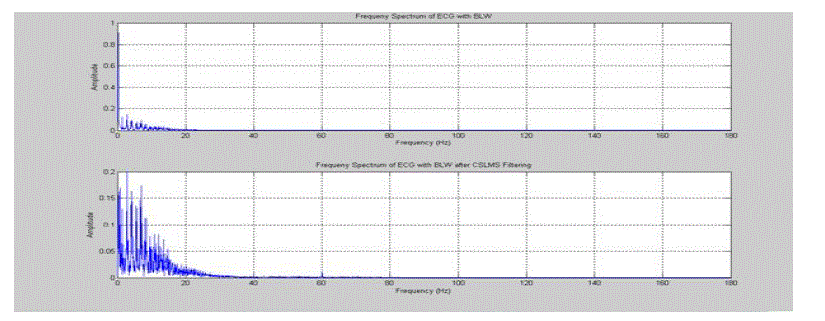
| To demonstrate power line interference (PLI) cancelation selected MIT-BIH record number 105. The input to the filter is ECG signal corresponds to the data 105 corrupted with synthetic PLI with amplitude and frequency 60Hz, sampled at 200Hz. The reference signal is synthesized PLI, the output of the filter is recovered signal. In SNR measurements it is found that CSLMS algorithm in figure.7 gets SNR improvement 6.6544dB, where as the LMS algorithm improves 6.5549dB. |
CONCLUSION FUTURE ENHANCEMENTS
|
| Both baseline wander and powerline interference removal are mainly a question of filtering out a narrow band of lowerthan- ECG frequency interference. The algorithm has been designed and implemented for both the least mean square (LMS) and CSLMS adaptive filter based upon the FIR filtering using MATLAB environment. The input and the desired response signals are properly chosen in such a way that the filter output is the best least squared estimate of the original ECG signal. The proposed treatment exploits the modifications in the weight update formula and thus pushes up the speed over the respective LMS based realizations. In simulations, confirmed that the performance of the CSLMS is better than the LMS algorithm in terms of SNR, MSE and frequency spectrum. CS-LMS algorithm can be effectively used in Sub-Band adaptive filtering applications in order to produce optimized response. Hence CSLMS based adaptive noise canceller may be used in all practical applications. This algorithm has also appreciable significance in speech processing. |
Figures at a glance
|
 |
 |
 |
 |
| Figure 1 |
Figure 2 |
Figure 3 |
Figure 4 |
|
 |
 |
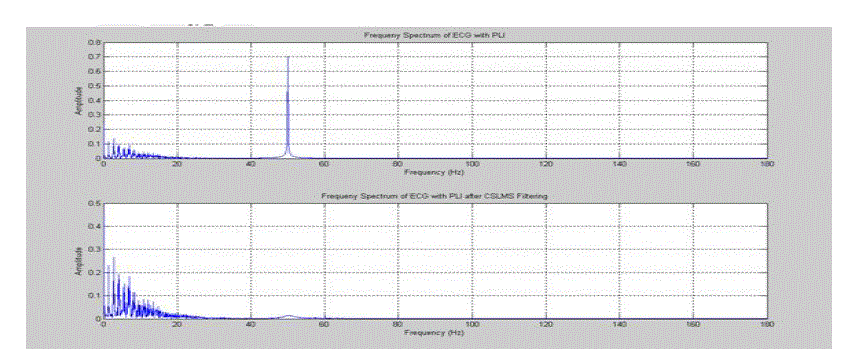 |
| Figure 5 |
Figure 6 |
Figure 7 |
|
References
|
- C. Brouse, G. A. Bumont, F. J. Herrmann, and J. M. Ansermino, "A Wavelet Approach to Detecting Electrocautery Noise in the ECG," IEEE Eng. Med. and BioI. Mag., Vol. 25, No. 4, pp. 76-82, 2006.
- Ching-An Lai, "NLMS Algorithm with Decreasing Step Size for Adaptive IIR Filters”, Signal Processing, Vol.82, PP. 1305-1316, 2002
- Floris. E, A. Schlaefer, S. Dieterich and A. Schweikard, “A Fast Lane Approach to LMS Prediction of Respiratory Motion Signals", Biomedical Signal Processing and Control, Vol.3, pp. 291-299,2008.
- G. Mihov and I. Dotsinsky, "Power-Line Interference Elimination from ECG in case of Non-Multiplicity Between the Sampling Rate and the Power line Frequency”, Biomedical Signal Processing and Control, vol. 3, pp. 334-340, 2008.
- J. E. Greenberg, "Modified LMS Algorithms for Speech Processing with an Adaptive Noise Canceller”, IEEE Transactions on Speech Audio Process, Vol. 6, pp. 338-351, 1998.
- M. H. Costa and C. M. Bermudez, “A Noise Resilient Variable Step-Size LMS Algorithm”, Signal Processing, Vol. 88, PP. 733-748, 2008.
- M. Kotas, "Application of Projection Pursuit Based Robust Principal Component Analysis to ECG Enhancement", Biomedical Signal Processing and Control, Vol.No.1, PP. 289-298, 2007.
- Ning Li, Y. Zhang, Yanling. H and J. A. Chambers, "A New Variable Step size NLMS Algorithm Designed for Applications with Exponential Decay Impulse Responses”, Signal Processing, Vol. 88, P. 2346-2349, 2008.
- S. Haykin, “Adaptive Filter Theory”, Englewood Cliffs, NJ: Prentice- Hall, 1986.
- Y.Der Lin and Y.Hen Hu, "Power-Line Interference Detection and Suppression in ECG Signal Processing", IEEE Transactions on Biomedical Engineering, Vol. 55, PP. 354-357, 2008.
|