In this paper, non-carrier based digital switching functions and patterns are developed using VHDL language (DSFPV).Non-Carrier based switching angle method is selected for the reduced distortion characteristics. Different methods of switching angle methods like equal phase method, half equal phase method, half height method and feed forward method are designed and developed using VHDL coding. These generated digital switching pulses are validated by interfacing with the 81-level Trinary Cascaded Hybrid Multi-Level Inverter (TCHMLI) simulink model. The obtained simulation results are analysed by the measure of Total Harmonic Distortion (THD), Peak Voltage (Vpeak), Root Mean Square Voltage (Vrms), Average Voltage (Vavg), Form Factor(FF) and Crest Factor(CF).
Keywords |
| Trinary cascaded hybrid multi-level inverter, switching angle methods, VHDL code, THD |
INTRODUCTION |
| Multi-level inverter is a device that converts Direct Current (DC) to Alternating Current (AC) with number of levels
resembling the sine wave. A multi-level power converter is an alternative in high power and medium voltage
applications. Multi-level inverter has several advantages in the field of power electronics like reduction in switching
losses, lower THD, enhanced Electro Magnetic Compatibility (EMC), reduced Electro Magnetic Interference (EMI)
and higher efficiency. The reduction of THD depends on the topology of multi-level inverter, its modulation schemes
and switching methods. |
| Multilevel voltage source inverter has arrangement of semiconductor switches and DC sources. The switches are
controlled to generate pulsed output sinusoidal waveform. Mostly switches in MLI are controlled by PWM strategies.
PWM switching control strategy enables the MLI to reach high voltage with low harmonics without the use of the
transformers. Increase in the number of voltage levels decreases the harmonic distortion of the output. Reduction in
harmonics distortion decreases losses and heat in motor drive applications. |
RELATED WORK |
| Different MLI topologies are designed which optimizes the power usage of the overall system by utilizing distinct type
of semiconductor and modulation strategies. A fundamental issue for a multilevel inverter is to find the switching
angles (times) of the inverter power switches that produce the required fundamental voltage and at the same time
eliminate or reduce the values of undesired specific low order dominant harmonics. Reduction of THD can be achieved
by using Mixed Integer Linear Programming (MILP) method at cost of high switching losses [1], switching angles
formulated by Fourier Series method [2] and the selective harmonics elimination method [3]. The MILP method aims
to minimize low order non-triplen odd harmonics starting from the 5th
harmonic. The triplen odd harmonics are self
cancelled in the output line voltage assuming a star connected three phase inverter. The total harmonic distortion
percentage (%THD) as well as the weighted total harmonic distortion percentage (%WTHD) is calculated from the
5th harmonics [1]. Switching angles formulated by Fourier series method can increase the number of voltage levels and
lower harmonic distortion with the same topology. The increase in the number of voltage levels leads to an
improvement in power quality and reduction on the size and power loss of filter [2].The VHDL codes are used in generation of modulating sinusoidal wave and carrier triangular wave for pulse width modulation to generate switch
patterns [4].The switch patterns were logically generated using c-code based on resultant theory [5] had advantage of
higher order harmonic reduction compared to the numerical method using newton raphson method. In this paper, a
digital mode of controlling the switches is designed to improve the performance of the whole system in terms of THD
and high power ratings. |
TRINARY CASCADED HYBRID MULTI-LEVEL INVERTER |
| Muli-level inverters are classified as (i) Diode Clamped type (ii) Flying Capacitor type (iii) Cascade type and
(iv) Hybrid type. Trinary Cascaded Hybrid Multi-Level Inverter (TCHMLI) is a hybrid type which uses unequal DC
link sources in each of its H-bridge circuits. Cascaded type trinary hybrid multilevel is used in this work as they require
less number of components than the other types. Cascaded MLI consists of a series of H-bridge inverter units which
synthesize a desired voltage from each separate DC source load voltage. TCHMLI never uses clamping diode and
flying capacitor in its circuit. TCHMLI uses less number of redundant components, a modular structure, no issue of
voltage balancing, and level extend is very simple [6]. |
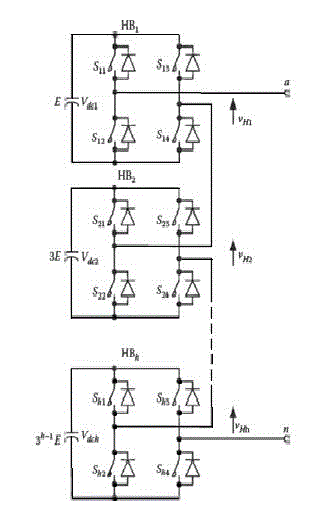
| In this work, a single phase TCHMLI is used to generate the 81-Levels DC link voltages in the ratio of 1:3:9:........:3i-1;
where “i” is the number of H-bridges is based on the equation. |
 |
| It has four H-bridges in its structure, which has four switches and a DC link source in each H-bridge is shown below in
fig.1 |
| The switching functions for the 81-level TCHMLI are obtained based on the switching combinations of the DC
link sources. The switching function for each H-bridge is designed to out a positive DC value when the switches Si1 &
Si4 are turned ON, a negative DC value when the switches Si2 & Si3 are turned ON and a zero value when either Si1 &
Si3 are turned ON or Si2 & Si4 are turned ON. Generally these switching functions are generated using pulse width
modulation strategy like phase disposition, alternate phase disposition, and in phase disposition which provides high
power with low harmonics [7].In this work switching functions are designed using switching angle methods. The
development of switching patterns to generate 81 DC levels using switching angle method is explained in the following
section. |
PROPOSED SWITCHING ANGLE METHOD |
| Multi-level inverter is designed for different topologies using several techniques with many advantages. An improper
arrangement of switching angles in MLI could not generate an efficient AC output waveform. The Switching Angle
method is utilized for the evaluation of angles to generate the different DC levels in the multi-level inverter and reduce
THD. |
| The switching angle method enables the multi-level inverter to generate an output resembling the sinusoidal wave. The
switching angle method is a non-carrier based method; hence no modulation schemes for the generation of switching
pattern are required. Switching angle is the point or event at which the multi-level inverter proceeds from one level to
the next level. The switching angle method is a technique which formulates all events that occur within one cycle to
change the output of the multi-level inverter. Once all these switching angles are derived, the sequence for switch
patterns is formatted as required by the type of “m-level” multi-level inverter. |
| The switching angle method divides the multi-level inverter output into four quadrants in angles.
(i) First Quadrant (0°-90°) (ii) Second Quadrant (90°-180°) (iii) Third Quadrant (180°-270°) and
(iv) Fourth Quadrant (270°-360°).The evaluations of switching angles in each of these quadrants are relatively simple
and interlinked. |
 |
| This switching angle estimation is validated by implementing in four methods. They are |
| (i) Equal Phase Method (EPM): The switching angles are estimated and arranged with equal space from 0 to π. |
| (ii) Half Equal Phase Method (HEPM): The switching angles are calculated and placed with equal space in alternate
angles. |
| (iii) Half Height Method (HHM): The switching angles are manipulated and assigned with equal space till the half of
the multi-level inverter output and with equal space in alternate angles above the half of the multi-level inverter output. |
| (iv) Feed Forward Method (FFM): The switching angles are derived and designated with equal space till the quarter
of the multi-level inverter output such that the wider gap between the positive half cycle and negative half cycle is
reduced than the above three methods. |
DSFPV ALGORITHM |
| Very High Speed Integrated Circuit Hardware Description Language (VHDL) allows modelling the behaviour of the
required system and verifying it by simulation before getting synthesized. VHDL is used for the design of 81-Level
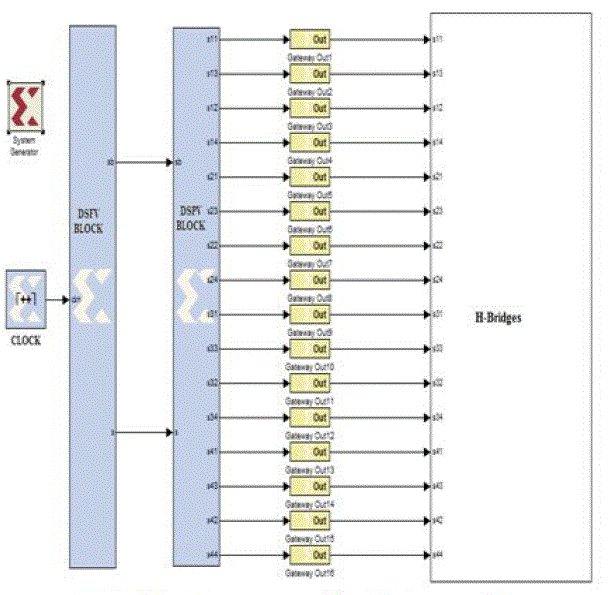
TCHMLI. In fig.2, the DSFPV has two blocks namely Digital Switching Function using VHDL code (DSFV block)
and Digital Switching Pattern using VHDL code (DSPV block) to generate the switching functions and patterns.
For the 81-level TCHMLI, there are 40 switching angles in each of the four quadrants which are calculated for all the
four switching angle methods. These 160 switching angles are converted into 29 bit equivalent. The DSFV block
designed by VHDL coding, outputs the 80 voltage levels in which 40 for positive half cycle and 40 for negative half
cycle as shown in Table.1 |
| In the DSPV block, the 80 voltage levels and a zero voltage level are combined logically to generate the patterns
required for the 16-switches in the H-bridges of 81-level TCHMLI. The 16-switching patterns are interfaced with the
developed TCHMLI MATLAB SIMULINK model to get the sinusoidal output with reduced THD. Fig.3 explains the
design flow for DSFPV algorithm. The designed switching pattern are verified by XILINX tool in Matlab and validated
by interfacing with the cascaded hybrid multi-level inverter model developed using SIMULINK. POWER SYSTEM
BLOCK SET. |
RESULT AND DISCUSSION |
| Simulation of 81-level TCHMLI is done using SIMULINK Power System Blockset. The trinary dc link sources used
are Vdc1 = 5E, Vdc2=15E, Vdc3=45E and Vdc4=135E V. Simulation results validating the different angle methods using
the proposed DSFPV algorithm are presented. |
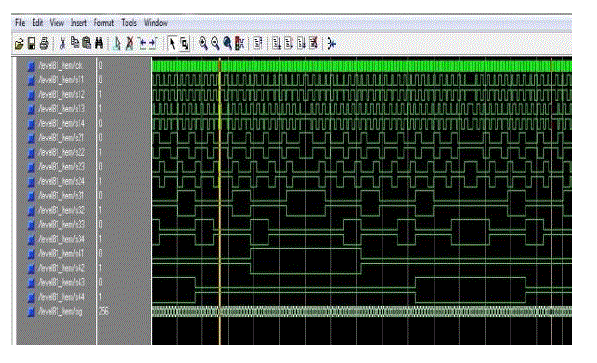
| Fig.4 shows the digital switching pattern for the TCHMLI using EPM. In the EPM, the switching angles are arranged in
the range of 0 to π. |
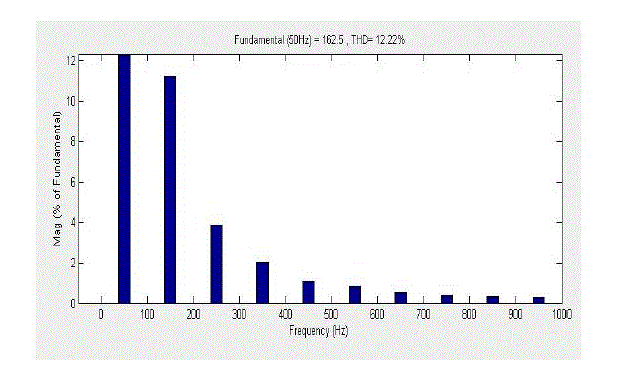
| Fig.5 and Fig.6 show the simulation output and the THD of 12.22% for the 81-level TCHMLI-EPM. |
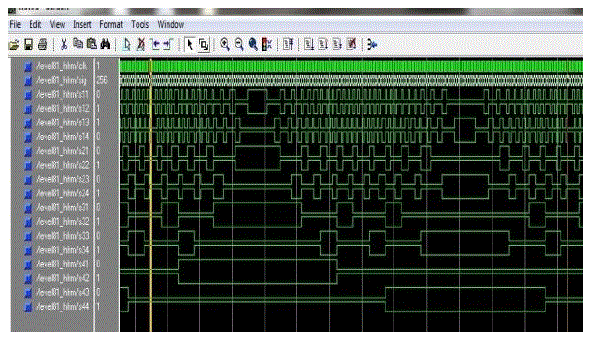
| The digital switching pattern for the 81-level TCHMLI using the switch pattern HEPM is shown in Fig.7. |
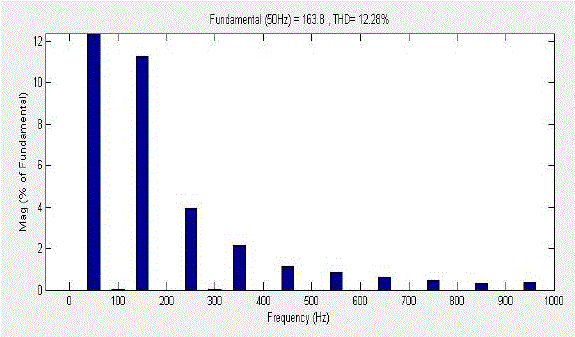
| Fig.8 shows the 81-level output waveform of TCHMLI using the switch pattern HEPM and the THD of the HEPM is
found to be 12.28% as shown in Fig.9. The simulated 81-level output waveforms of TCHMLI using EPM and HEPM
depicts the fact that none of the above methods were close to a sinusoidal waveform. This problem was rectified by the
design of 81-level TCHMLI using HHM. |
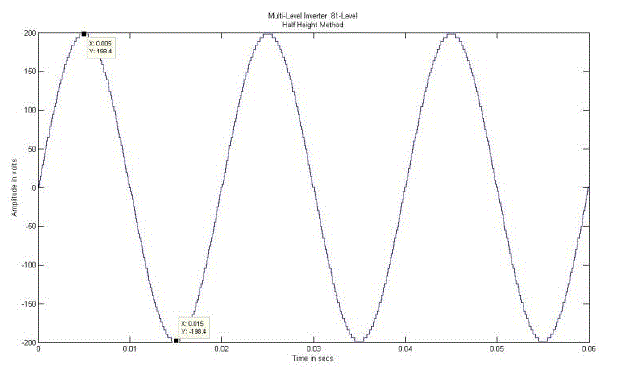
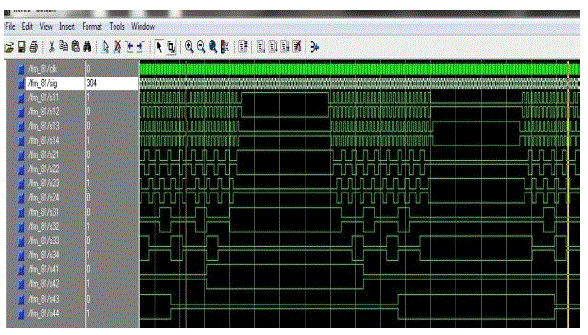
| Fig.10 shows the digital switching patterns. The output obtained from the DSFPV algorithm using this method is close
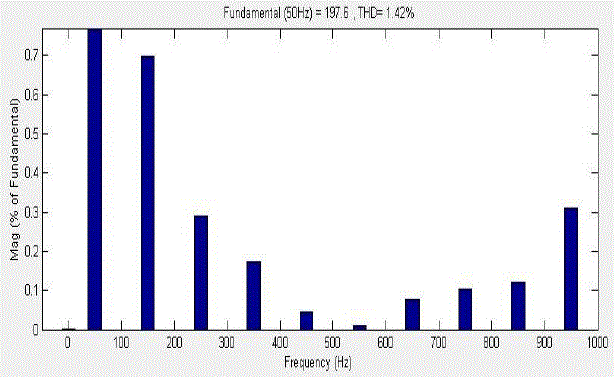
to a sinusoidal waveform and is shown in Fig.11 and Fig.12 shows the THD value of the HHM as 1.42%. |
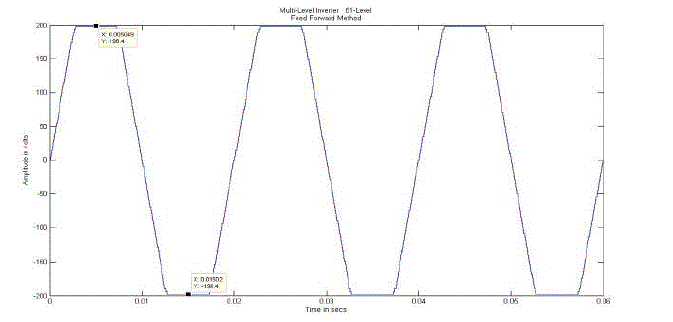
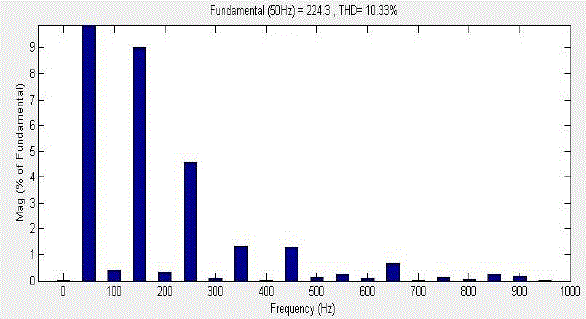
| The 81-level TCHMLI is designed by using the switch pattern FFM as shown in Fig.13. The 81-level output waveform
of TCHMLI using FFM is presented in Fig.14.The 81-level output waveform of TCHMLI using FFM as shown in
Fig.15 has more duration for its peak level ,hence its THD is 10.33%. |
| The switching angle methods designed by DSFPV algorithm can be easily implemented using FPGA in the future. This
DSFPV algorithm is flexible to synthesize and provide a new way of implementing the TCHMLI with less design
complexity. The different switching angle methods are developed for the different levels say 9-level, 27-level, 81-level
of TCHMLI. The simulated results for each 9,27,81-level TCHMLI are analysed by the performance measure Vpeak,
Vrms, Vavg, THD,FF and CF are shown in Table 2. |
CONCLUSION |
| In this paper non-carrier based switching angle method digital switch patterns were generated using VHDL coding to
produce the sinusoidal output waveforms for improving the power quality of trinary mode cascaded hybrid type MLI.
Performance factors like THD related to power quality issues and Vrms, Vavg, Vpeak related to DC bus utilization
were evaluated and analysed. TCHMLI using HHM method is found to be satisfactory with more than ten times
reduction of THD from 12.28% to 1.42% in 81-level MLI, from 15.44% to 3.67% in 27-level MLI, from 20.96% to
10.13% in 9-level MLI. Table 2 implies the inverse relationship between the number of levels and THD.TCHMLI
using FFM method is found satisfactory for DC bus utilization. Therefore the MLI for a particular application based on
output voltage quality and distortion level reduction can be selected. |
Tables at a glance |
 |
 |
| Table 1 |
Table 2 |
|
Figures at a glance |
 |
 |
 |
 |
| Figure 1 |
Figure 2 |
Figure 3 |
Figure 4 |
 |
 |
 |
 |
| Figure 5 |
Figure 6 |
Figure 7 |
Figure 8 |
 |
 |
 |
 |
| Figure 9 |
Figure 10 |
Figure 11 |
Figure 12 |
 |
 |
 |
| Figure 13 |
Figure 14 |
Figure 15 |
|
References |
- M.El-Bakry, “Minimizing Harmonics Values in Non-Uniform Step Asymmetric CMLIs”, Volume 2, Issue 10, 2012.
- Zixia Sang, Chengxiong Mao, and Dan Wang, “Staircase Control of Hybrid Cascaded Multi-Level Inverter” Electric Power Components and Systems, Taylor & Francis Group, Vol 42(1),pp.23-34, 2014.
- Jagdish Kumar and Er.Nishant, “Selective Harmonic Elimination Technique for a CMLI with Unequal DC Sources”, Proceedings of the World Congress on Engineering 2013 Vol II, WCE July 2013.
- S.Mekhilef and A.Masaoud, “Xilinx FPGA based Multilevel PWM Single Phase Inverter” ,Vol.1,No 2 pp 40-45,December 2006.
- John Chiasson, Leon Tolbert, Keith Mckenzie and Zhong Du, “ Eliminating Harmonics in a Multilevel Converter using Resultant Theory”University of Tennessee,2005.
- Jih-Sheng Lai, Fang Zheng Peng, “Multilevel Converters-A new breed of Power Converter” IEEE/Industrial Application Society conference, Orlando, FL (United States), 8-12 Oct 1995.
- S.A.Bashi, N.F.Mailah, M.Z.Kadir.K.H.Leong, “Generation of Triggering Signals for Multilevel Converter”, European Journal of Scientific Research.ISSN 1450-216X Vol.24.No.4,pp.548-555, 2008.
|