ISSN ONLINE(2319-8753)PRINT(2347-6710)
ISSN ONLINE(2319-8753)PRINT(2347-6710)
Gaurav Rastogi1, Khalid Moin2, S.M. Abbas3
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology
A 3 storey reinforced concrete frame of 1:4 scale having brick infills was fabricated and push over test under cyclic loading with displacement control was performed. The structure was symmetric in plan and having brick infills at upper two floors. Free vibration test were also performed at different storey drifts to evaluate the frequencies and damping ratios. To observe the actual inelastic response of the structure, different nonlinear parameters like ultimate strength, ductility factor, cumulative energy dissipated and equivalent viscous damping were evaluated with the help of experimental results. These parameters are used to update the analytical results from a nonlinear analysis program SAP 2000 for reinforced concrete frame. With the updated analytical results, the nonlinear behavior and ultimate strength of the whole structure along with the vertical distribution of strorey drifts can be predicted with good reliability
Keywords |
| Inelastic response, Push over test, Nonlinear Analysis, Reinforced Concrete Frame, Masonry infill walls. |
I. INTRODUCTION |
| Seismic response of Reinforced Concrete frame structures has been one of the major topic of interest for past few years among the structural engineering researchers. The complex behavior of the Reinforced Concrete structures and their vulnerability to earthquake are the main cause behind this interest. Reinforced Concrete frame buildings with masonry infill walls have been widely constructed for industrial, institutional, commercial and residential uses in seismic prone regions worldwide. These masonry infill walls are generally not considered in the design process and are treated as non structural components. However the masonry walls have a significant increase in structural strength and stiffness as compared to a bare Reinforced Concrete frame. |
| The behaviors of building structures when subjected to severe earthquakes may undergo nonlinear plastic deformations. Inelastic behavior of Reinforced Concrete frame structures plays a vital role in the current seismic design and requalification practice for Reinforced Concrete structure. In this practice the non linearity of the structure in linear analysis is indirectly taken into account by reducing the seismic demand on the structure or by a response reduction factor proportional to the expected ductility of the structure or sometimes some kind of non linear analysis such as pushover analysis or non linear time history analysis is performed to have a better estimate of demand on the structure due to seismic event. Nonlinear time history analysis is the most rigorous procedure to compute seismic demands, current civil engineering practice prefers to use the nonlinear static procedure or push over analysis in accordance to FEMA 356 document. Several studies in the past in [1], [2] and [3] have used the reduced scale models to examine the response of Reinforced Concrete frame structures. For experiments, the reduced scale models are always proved to be less costly in fabrication and testing than full scale models. Considering the limitations of test facility available, a three dimensional 1:4 scale model of a 3 storey Reinforced Concrete frame building structure with brick infill walls at two upper floors is fabricated according to the similitude law. Push over test under cyclic loading is performed with displacement control to experimentally observe the response of the Reinforced Concrete frame against lateral forces in the linear elastic and inelastic regions. |
II. SHORT REVIEW |
| In past few years, extensive experimental and analytical studies have been carried out on beam-column joint subassemblies, tested under quasi-static loading by [4], [5], [6], [7] and [8]. In most of the cases only constant axial load has been used, and the effect of the floor slabs and transverse beams has been neglected. Frame models have also been tested in last few years. The experiments reported by [9], [10] and [11], consist of 2D middle scale and full scale frames with and without floor slabs and transverse beams, tested quasi-statically. In the first experiment only 2:3 scale plain frames were tested. In the second investigation full scale interior frames with floor slabs were considered, whereas in the third study two 1 : 2.5 scale exterior frames jointed together by floor slabs were used to form a 3D structure. Now days several analysis computer programs [12] and [13], are available for the prediction of inelastic behaviors of the structures. Before using this technique as a sound and universal tool, it seems necessary to verify the credibility of these programs by investigating the correlation between the analysis and the experiments. There have been researches on this subject [14], [15] and [16]. However there have been very little researches on the updation of these programs to predict the actual response of the structures against lateral forces. Thus the main objective of this study is to update the analytical model to observe the actual inelastic response of the structure with the help of results obtained from the quasi static experiment. |
III. EXPERIMENTAL PROGRAM |
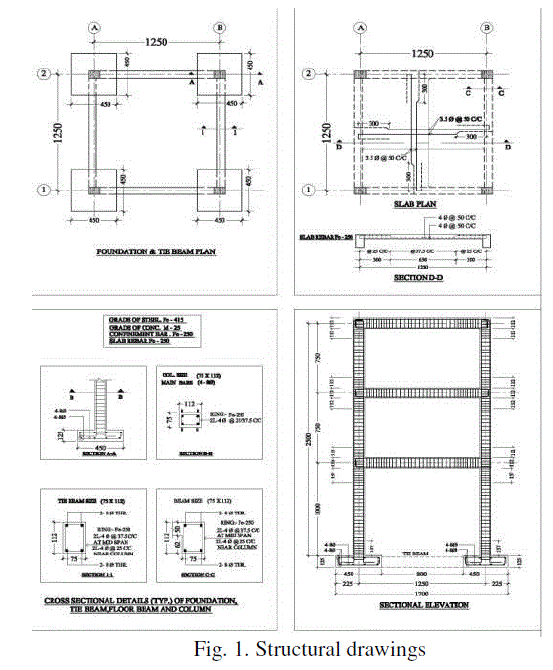 |
| The development of an experimental model should be able to represent accurate inelastic response of the proto type structure with the less degree of distortion. For this, scaled down proto type materials (aggregates size of the concrete and reinforcement diameter) are used to fabricate the 1:4 scale model of 3 storey Reinforcement Concrete frame with following the similitude requirements [17]. Physical /geometrical dimensions of the model are decided in accordance to the limitations of the quasi static test facility available. The details of experimental model are presented in Fig. 1. The Reinforcement Concrete 1:4 Scale model is designed as per IS 456:2000 [18] and IS 1893 (Part I):2002 [19]. |
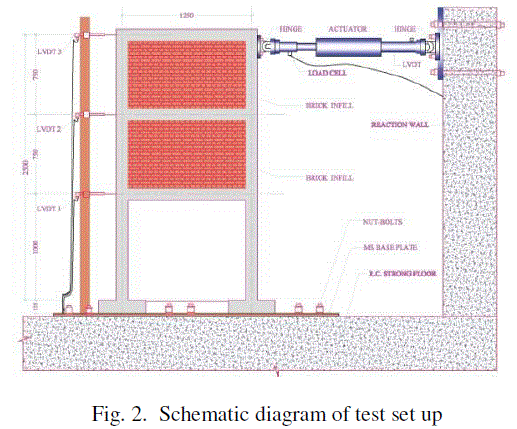 |
| Quasi static (Push over) and free vibration tests are conducted on the model. The schematic diagram of the test set up is shown in Fig. 2. The ranger seismometers are placed in both the perpendicular horizontal directions at the roof of model. The model is excited by the impact of a wooden hammer at the roof level and the free vibration records are recorded. Displacement controlled cyclic loading is applied at roof level of the model through actuator in increments of 2.5 mm of displacement in each cycle. Free vibration test is carried out at every 10mm displacement of the roof of the model. Push over test is performed till the model has lost the approximate 80% of its ultimate strength |
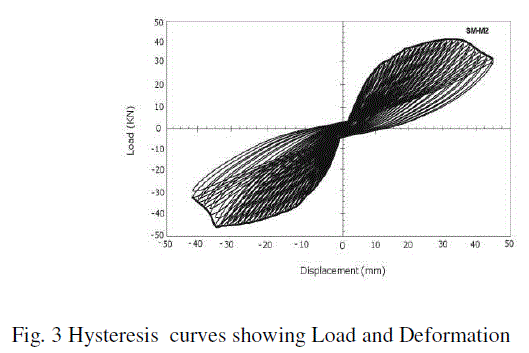 |
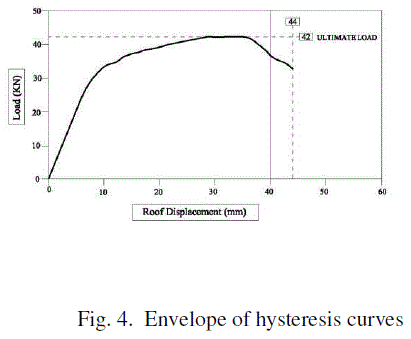
| The hysteresis curves and the envelope of the hysteresis behavior of the model in the form of load- deformation curve, is shown in Fig. 3 and 4 respectively. |
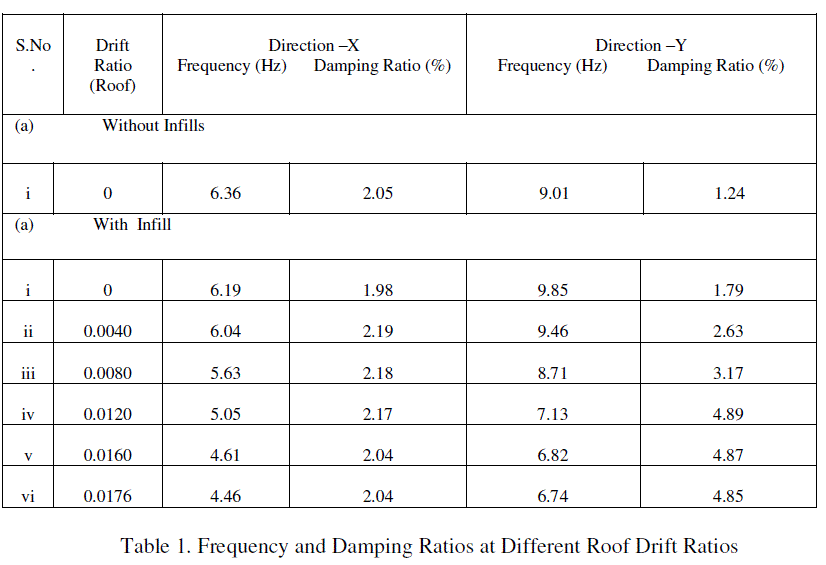 |
| Drift ratio, Frequency and Damping ratio are shown in Table 1. |
 |
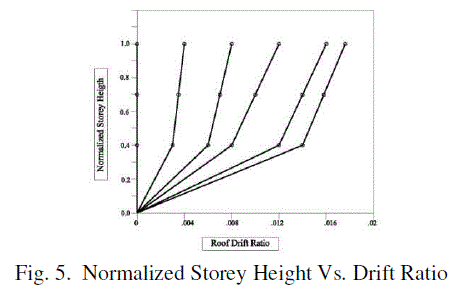
| The storey profiles with regard to roof drift ratio are shown in Fig. 5. |
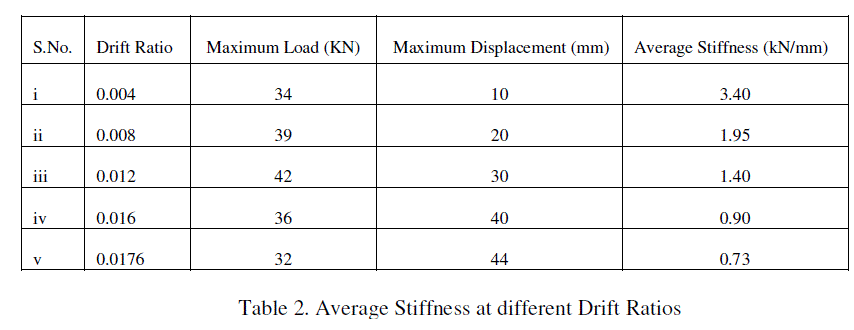 |
| Average stiffness at different drift ratios of the experimental model are shown in Table 2. |
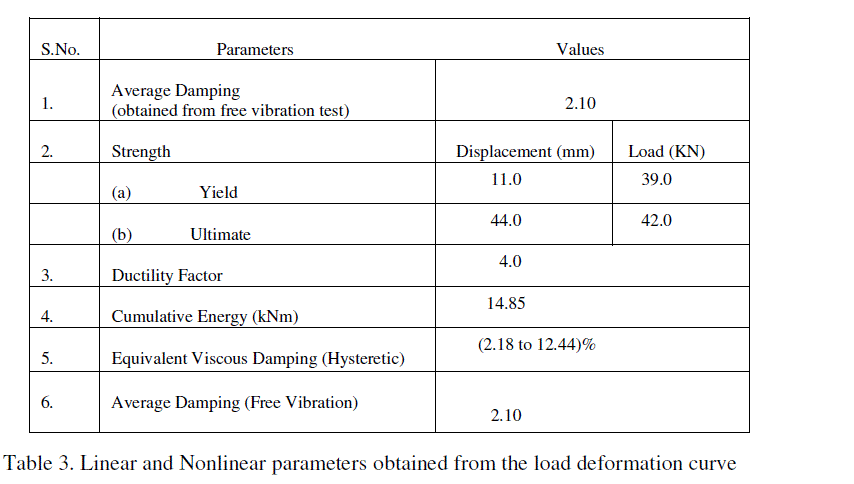 |
| Linear and nonlinear parameters as cumulative energy dissipation, equivalent viscous damping ratio and strength [20] are derived from the hysteresis curves and shown in Table 3. |
IV. UPDATING OF NONLINEAR ANALYTICAL 1:4 SCALE MODEL |
| The nonlinear analytical modeling of the same 1: 4 scale 3 storey Reinforced Concrete frame having equivalent struts for infill walls has been carried out using nonlinear analysis program SAP 2000 [21]. The accuracy of the results of nonlinear modeling depends on various input parameters as yield interaction, axial and flexural forces, moment, curvature and rotation characteristics for appropriate nonlinearity of the constitutive material etc. The push over loading along the height is also very important for proper estimation of nonlinear performance of the model. |
| In this study the nonlinear analytical model is developed on the basis of FEMA 356 guidelines [22], so that the nonlinear behavior of the structure during earthquake could be predicted with sufficient accuracy. The base shear- roof displacement curves and storey drift profile obtained from the results of Quasi Static Test under cyclic loading of the experimental model are used to update the nonlinear parameters of the analytical model in nonlinear ranges. |
| The damage pattern and failure mode of the model obtained from the experimental results are tried to be validate with updated nonlinear analytical model. The nonlinear hinges are introduced to the analytical model as per FEMA 356 guidelines in the following manner -: |
| i) Axial and Flexural Hinges at each end of the columns. |
| ii) Flexural Hinges at each end of beams. |
| iii) Axial Hinges at center of equivalent strut used for infills. |
 |
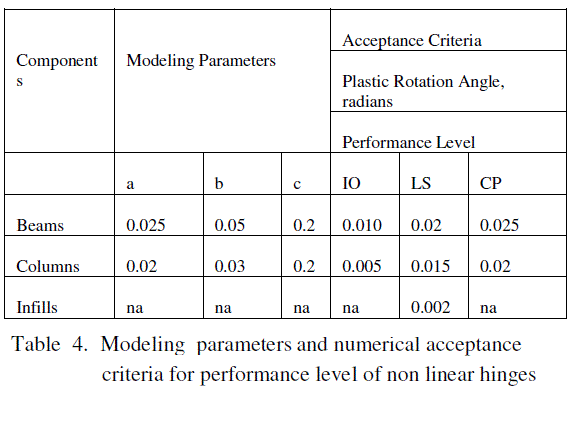 |
| Table 4. Modeling parameters and numerical acceptance criteria for performance level of non linear hinges |
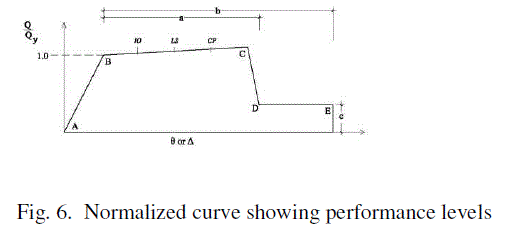
| The values of plastic rotation of each component of the analytical model have been modified in different trials for the best matching of push over curves with load deformation curves as obtained from experimental results. The acceptance criteria for different performance levels have been adopted as per FEMA 356 guidelines as shown in Fig. 6 and Table 4. |
 |
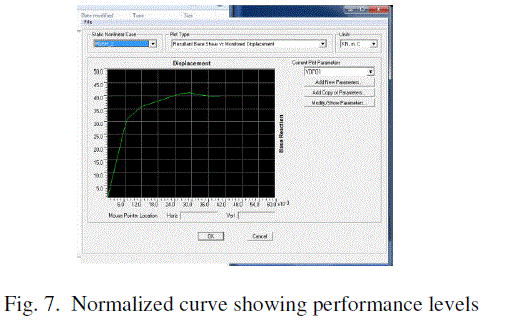
| Finally the nonlinear push over analysis of analytical model has been carried out using the above parameters and keeping the loading pattern same as applied in Quasi Static Test. The push over curves obtained analytically is shown in Fig. 7. |
V. COMPARISON AND VALIDATION OF THE RESULTS FROM ANALYTICAL AND EXPERIMENTAL TEST |
 |
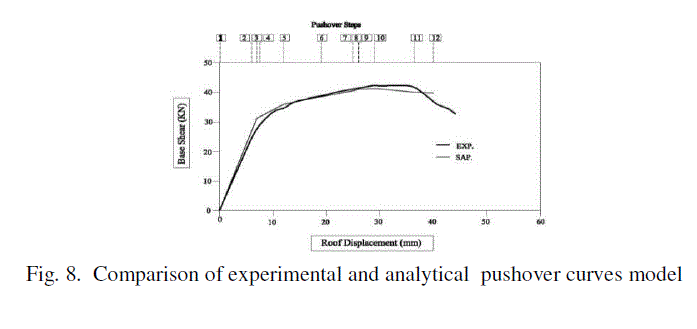
| The pushover curve is superimposed with envelope of hysteresis curves obtained from experiments and shown in Fig. 8. The modifications of controlling nonlinear parameters have been done to match both the curves within an acceptable percentage of error. The percentage of error over the entire displacement is divided into three ranges as - linear range i.e. upto yield, nonlinear range i.e. yield to ultimate and failure stage i.e. beyond ultimate. |
 |
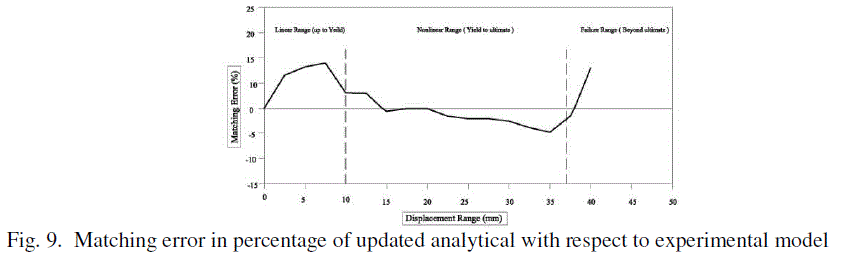
| A curve showing percentage of error in above 3 ranges has been plotted and shown in Fig. 9. The curve indicates that percentage of error is limited to 9% in linear range. This percentage of error may be due to approximate effective stiffness of the components. The percentage of error in nonlinear range is observed very low and limited to 5%. In failure stage the percentage of error increases upto 8%. |
 |
| The comparison of storey displacement profile along the height of the model obtained analytically and experimentally from Quasi Static Test results has been shown in Fig. 10. The Fundamental frequency of the analytical model is found to be nearly same as the frequency of the experimental model obtained from free vibration test.It is also observed during the pushover test, that state of stresses in infill masonry is different along the height. However the modeling of infill is the same, irrespective of its location and position along the height. Further, the information of nonlinear hinges obtained from updated nonlinear analytical model have been compared with damage pattern occurred in experimental model during Quasi Static Test under cyclic loading. The formation of nonlinear hinges in the updated analytical model is observed to be similar in sequence of damage pattern observed during testing of model under cyclic loading. |
VI. CONCLUSION |
| Based on the investigation, updation and validation between the analytical and experimental response of a 1:4 scale 3 storey Reinforced Concrete frame having brick infills, the following conclusions can be drawn - : |
| 1. The nonlinear modeling of Reinforced Concrete buildings and the updating inelastic properties, can assess the actual behavior under linear and nonlinear range. A close analytical matching of experimental cyclic performance in terms of pushover curves as well as the corresponding storey profiles can be obtained. |
| 2. The ultimate strength of the whole structure and the vertical distribution of storey drifts can be predicted with good reliability. |
| 3. The sequence of formation and the distribution of nonlinear hinges are similar to the test results. The performance of the structure during an earthquake can be assessed better by minor modification in the nonlinear parameters. |
References |
|