International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Menu

ISSN ONLINE(2278-8875) PRINT (2320-3765)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

Novel Bi-Orthogonal Filter Coefficient Wavelet Transform for Image Compression

B. Sivachandra mahalingam, Pranav priyadarshi prince, Ganga Shankar kumar
  1. Assistant professor (Gr-II), Department of ECE, Aarupadai Veedu Institute of Technology, Paiyanoor, Tamlinadu, India
  2. UG student, Department of ECE, Aarupadai Veedu Institute of Technology. Paiyanoor, Tamlinadu, India
  3. UG student, Department of ECE, Aarupadai Veedu Institute of Technology. Paiyanoor, Tamlinadu, India
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Abstract

This thesis implements the TDM method and presents performance results for orthogonal and biorthogonal wavelets using both periodic and symmetric extension techniques . Our results for symmetric extension indicate a slight performance advantage for biorthogonal wavelets (particularly for low frequency images); this advantage is significantly smaller than recently published results. Our analysis also demonstrates the importance of linear phase filters on image compression performance



INTRODUCTION
The discrete wavelet transform (DWT) has been applied extensively to digital image processing, especially transform coding of digital images and digital image sequences. Since images are mostly smooth (except for occasional edges), it seems appropriate that the wavelets should be reasonably smooth, which requires the associated filters to be long enough to obtain smoothness and energy compaction capability. However this will increase the computational cost of the corresponding transformation. 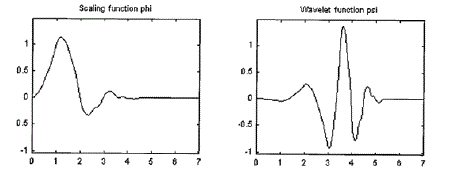On the other hand, it is desirable that the finite impulse response (FIR) filter bank (FB) be linear phase (corresponding to symmetry for wavelets and scaling functions). Unfortunately, it has been shown that orthogonality and symmetry are conflict properties for design of compactly supported nontrivial wavelets.
The highly important linear phase constraint multiplication - free DWT/IDWT algorithm using some short spline wavelet systems was proposed.
However, in general the compression performance of the bi -orthogonal spline wavelet systems is worse than that of the CDF-9-7 FB. Therefore, in coding applications, choosing a wavelet system seems a trade off between compression performance and computational complexity. In 1989, Coiffman proposed the idea of constructing orthonormal wavelets with vanishing moments equally distributed for the scaling function and wavelet. Such wavelets, so called coiflets, These observations may suggest that if we relax orthogonality and keep vanishing moments equally distributed for scaling function and wavelet it might be possible to obtain less asymmetric, or exactly symmetric, biorthogonal wavelet systems. A generalization of coiflets to the bi- orthogonal setting was introduced and a family of bi-orthogonal Coifman wavelet systems, parameterized by the same degree of moments for both two scaling functions and both two wavelets, was developed. In particular, the coefficients of the associated dual filters were all dyadic rational numbers with specific formulae for all orders.

SIGNIFICANCE OF THIS WORK
Matrix based methods have demonstrated a technique for a DWT implementation with symmetric extension using orthogonal wavelets . However, these methods have not been evaluated in the literature. Also, in the past, the performance results of orthogonal wavelets using periodic extension has been compared To biorthogonal wavelets with symmetric extension . The comparison of subjective and objective performance of similar Orthogonal and biorthogonal wavelets employing symmetric extension for different image types has also not been reported in The literature .

OVERVIEW OF WAVELET BASED IMAGE COMPRESSION SYSTEM
Image compression is one of the most visible applications of wavelets. The rapid increase in the range and use of electronic imaging justifies attention for systematic design of an image compression system and for providing the image quality needed in different applications.
A typical still image contains a large amount of spatial redundancy in plain areas where adjacent picture elements (pixels, pels) have almost the same values. It means that the pixel values are highly correlated. In addition, a still image can contain subjective redundancy, which is determined by properties of a human visual system (HVS). An HVS presents some tolerance to distortion, depending upon the image content and viewing conditions. Consequently, pixels must not always be reproduced exactly as originated and the HVS will not detect the difference between original image and reproduced image.
The redundancy (both statistical and subjective) can be removed to achieve compression of the image data. The basic measure for the performance of a compression algorithm is compression ratio (CR), defined as a ratio between original data size and efficient coding, but requires more computational power. Image distortion is less annoying for small than for large DCT blocks, but coding efficiency tends to suffer. Therefore, most existing systems use blocks of 8X8 or 16X16 pixels as a compromise between coding efficiency and image quality. In recent times, much of the research activities in image coding have been focused on the DWT, which has become a standard tool in image compression applications because of their data reduction capability.
In a wavelet compression system, the entire image is transformed and compressed as a single data object rather than block by block as in a DCT-based compression system. It allows a uniform distribution of compression error across the entire image. DWT offers adaptive spatial-frequency resolution (better spatial resolution at high frequencies and better frequency resolution at low frequencies) that is well suited to the properties of an HVS. It can provide better image quality than DCT, especially on a higher compression ratio. However, the implementation of the DCT is less expensive than that of the DWT. For example, the most efficient algorithm for 2-D 8x8 DCT requires only 54 multiplications, while the complexity of calculating the DWT depends on the length of wavelet filters.
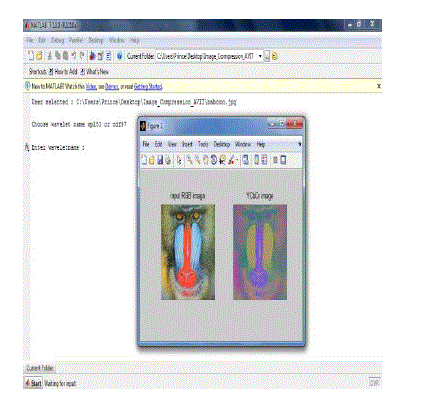
image
A wavelet image compression system can be created by selecting a type of wavelet function, quantizer, and statistical coder. In this paper, we do not intend to give a technical description of a wavelet image compression system. We used a few general types of wavelets and compared the effects of wavelet analysis and representation, compression ratio, image content, and resolution to image quality. According to this analysis, we show that searching for the optimal wavelet needs to be done taking into account not only objective picture quality measures, but also subjective measures. We highlight the performance gain of the DWT over the DCT. Quantizers for the DCT and wavelet compression systems should be tailored to the transform structure, which is quite different for the DCT and the DWT. The representative quantizer for the DCT is a uniform quantizer in baseline JPEG, and for the DWT, it is Shapiro’s zero tree quantizer. Hence, we did not take into account the influence of the quantizer and entropy coder, in order to accurately characterize the difference of compression performance due to the transforms (wavelet versus DCT)c

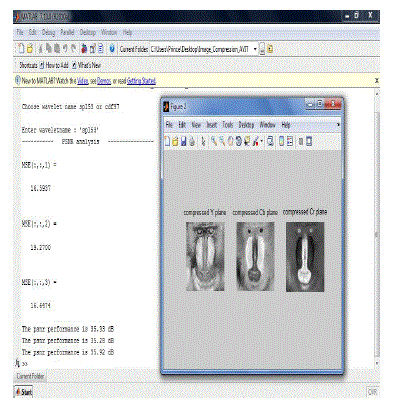
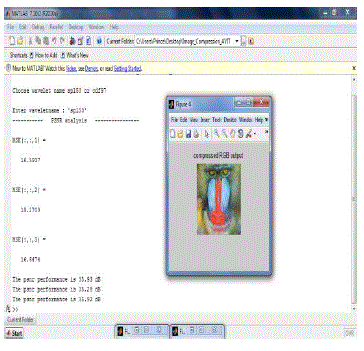
PERFORMANCE ANALYSIS AND RESULTS
The results presents in this thesis compare the image compression performance of periodic and symmetric extension techniques using the TDM nonexpensive DWT method. A 5-level DWT decomposition is followed by SPIHT quantization. Both objective as well as subjective performance of the compressed image are evaluated. The objective performance is measured by peak signal-to-noiseratio (PSNR) of the reconstructed image ~x. PSNR measured in decibles (dB) is given by:
PSNR = 10 log10 255 MSE !; where the value 255 is the maximum possible value that can be attained by the image signal. Mean square error (MSE) is defined as PSNR is measured in decibles (db). It has been shown that PSNR is not always a indicator of the subjective quality of the reconstructed image [24]. We also evaluate the subjective performance by visible artifacts in the reconstructed image.

CHOICE OF WAVELETS AND IMAGES
We employ 7 LA orthogonal daubechies wavelets, 7(A) orthogonal daubechies wavelets and 2 biorthogonal wavelets. It has been shown in chapter 3 that the least asymmetric wavelets and the corresponding asymmetric wavelets differ only in the GDD parameter.
Hence, by performance comparison of LA and A wavelets, we illustrate the importance of linear phase on compression performance. We then chose the best performing orthogonal wavelets and compare their compression performance against similar biorthogonal wavelets when both use symmetric extension.
The compression performance is evaluated for twelve grayscale images that can be grouped into three image types: four low frequency (LF) (Lena, peppers, boat, goldhill), four medium frequency (MF) (Barbara, lighthouse, Nitf7, House), four high frequency (HF) (Sattelite, Mandrill, Grass, SanDiego) images.
The frequency type groups are based on the percentage of total images energy (96% - 100% LF, 92% - 96% MF and 92% HF) in the LL subband obtained after one level of decomposition using the wavelet. The distribution of energy for the twelve image.

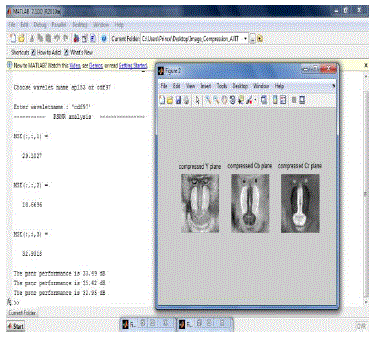
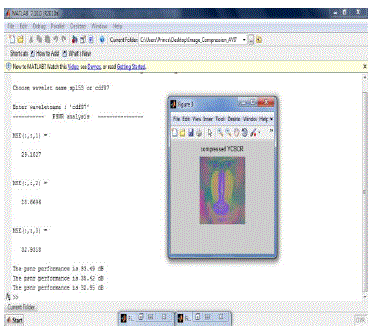
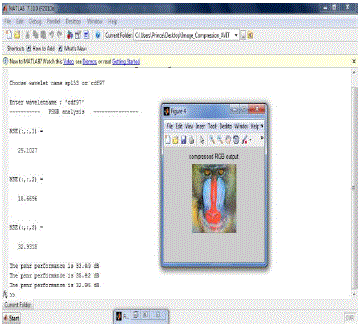
PSNR RESULTS
image
Where L and J are filter length and number of decompositions respectively. For, simplicity we consider only composition required for calculating the wavelet transform. For example, for a 256 * 256 image decomposed J = 5 and L = 10, the complexity will be approximately 3.5 million operations (MOP).

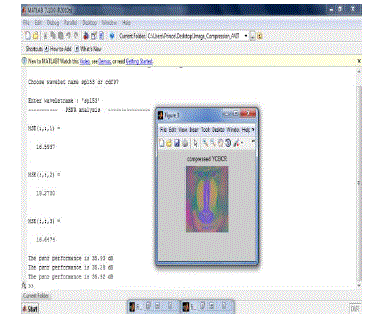
SUBJECTIVE RESULTS FOR SYMMETRIC EXTENSION
image
image
image
image
image
image
image

ITERATIVE DECOMPOSITION
The preceding chapter was concerned with only one scale decomposition of images. The test images were decomposed into four quadrants where the optimization of filters and testing took place. Such one scale iteration is not used for practical image compression intentions, rather the iteration process is repeated with decompositions of low – low sub – images several times.
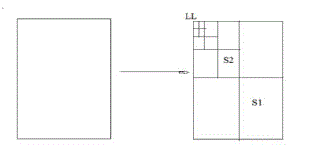image
Image decomposition L: f (x, y) R: w(x, y)
In this chapter we concentrate on weighted type B lters, as they gave the most qualified results, and try to implement a 4 level dyadic iteration of the low frequency zone; this divides the image into a total of 13 different subzones. We denote the LH/HL/HH zones of the rst iteration for s1, the subbands of the second iteration for s2 and so on till s4. The LL zone ( include in s4) corresponds to the small quadrat on upper left. For the 256 * 256 test image low – low subimage consist of 16 * 16 pixels.

TEST IMAGES
image
image
image

EQUAL WEIGHTS
Selecting equal weights Q1 = Q2 = Q3 =Q4 is a straight forward option and table 7.3 shows the outcomes in this circumstance ; 9 -7 filter with all the loads at 1000. Equal loads for S1, S2, S3 and S4 (LL excluded) can easily be seen as not being a reasonable choice for the optimization as with iterations the quantity of energy in the subbands increases, this must be allowed and tolerated by selecting decreasing loads for the iterative subzones.

WEIGHTS RELATIVE TO THE AREA
A different weight selection for Q1; Q2; Q3 and Q4 can be related with the number of pixels they cover . the outer zone S1 covers three quarter of the image while S2 only one fourth of this, 3 44. The S3 part 3 444 while S4 (ignoring LL) conceals 3 444 part of the image. The weights can therefore be multiplied relative to the field. Starting with Q4 = 1000 one obtains Q3 = 250, Q2 = 62:5, and Q1 = 15:6.

9/7 FILTERS
Selecting this optimization method we constructed optimized 9 – 7 filters for all three test images, the outcomes from the decompositions are in table 7.4. the average entropy values are not any better than under CDF 9 – 7, however, together the total energy in S1, S2 and S3 compared with the CDF filter is lower for the optimized filter and likewise is the situation for the entropy in these zones. The artificial M3 image though is an exception. Still, one does not observe any large energy increases for the S4 zone and the effect of energy shifting seems to be minimal, on the contrary one notices a power increases for the S1 area.

ITERATIVE DECOMPOSITION
With Q = 1000 this optimization strategy returns = 0:3214 for M2 and = 0 : 2564 for M3 and 9 – 7 filter pair. The value for M3 is very different from the others as this pictue is clearly distinctive from the rest. The emphasis of this chapter has been on designing optimized seperable filters for images which would transfer as much energy as possible to the low – low subimage. We investigated different models of type a filter and with stability limits one can quite acceptable filters.
For weighted type B filters on the hand other the stability problem more or less vanishes and filters can manage to shift considerable energy away from the high - high frequency zone. For many natural images this can gives extra gains for lossless entropy coding. The weights for high frequency images can also be set up in such a way to minimize to total energy or the average entropy by implementing a double optimization.
By changing the optimization criteria and selecting weights relative to the total area covered by a subbands, optimized filters can be designed with reasonable coding property. Such algorithm can be used to design filter which can yield slightly higher PSNR values at the same or lower b = p coding rates compared with some traditional filters.

CONCLUSIONS AND FUTURE WORK
We have presented the design of a novel class of bi orthogonal wavelet systems, the GBCW systems, which possess several remarkable properties. In particular, three FB’s in this family have been shown to be competitive with the CDF-9-7 FB in DWT-based image compression. Furthermore, the multiplication-free DWT/IDWT using the GBCW systems are promising in the realization of real-time image and video codec.
In this paper, we have proposed a hybrid scheme combining Kohonen’s Self Organizing Feature Map (SOFM) based Vector Quantization (VQ) coding and Set Partitioning In Hierarchical Trees (SPIHT) coding for effectual compression of images. Initially, the input image has been subjected to bi orthogonal wavelet transform. Then, the decomposed image has been compressed using SPIHT encoding, which outputs a bit stream. Subsequently, the resulted bit stream is fed to the SOFM based VQ coding for further compression. The SOFM algorithm has generated a codebook corresponding to the inputted bit stream and then based on the generated codebook has effectively compressed the bit.
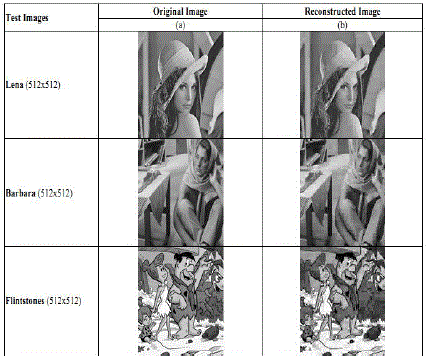
A Hybrid Coding Scheme Combining SPIHT and SOFM Based Vector Quantization for Effectual Image Compression 438 stream to attain the final encoded data. The original image has been reconstructed with the linear combination of its corresponding processes as in image encoding. The reconstructed image qualityachieved after decoding has been of desirable quality. The experimental results have portrayed theeffectiveness of the proposed hybrid scheme in image compression.
In this paper, we presented results from a comparative study of different wavelet-based image compression systems. The effects of different wavelet functions, filter orders, number of decompositions, image contents, and compression ratios are examined. The final choice of optimal wavelet in image compression application depends on image quality and computational complexity. We found thatwavelet-based image compression prefers smooth functions of relatively short length. A suitable number of decompositions should be determined by means of image quality and less computational operation.
Our results show that the choice of optimal wavelet depends on the method, which is used for picture quality evaluation. We used objective and subjective picture quality measures. The objective measures such as PSNR and MSE do not correlate well with subjective quality measures. Therefore, we used PQS as an objective measure that has good correlation to subjective measurements.
Our results show that different conclusions about an optimal wavelet can be achieved using PSNR and PQS. Each compression system should be designed with respect to the characteristics of the HVS. Therefore, our choice is based on PQS, which takes into account the properties of the HVS. We analyzed results for a wide range of wavelets and found that BW-2.2 provides the best visual image quality for different image contents. Additionally, BW-2.2 has very low computational complexity in comparison with the other wavelets. BW- 2.2 is used in analysis and comparison with DCT. Although DCT processing speed and compression capabilities are good, there are noticeable blocking artifacts at high compression ratios. However, DWT enables high compression ratios while maintaining good visual quality. Finally, with the increasing use of multimedia technologies, image compression requires higher performance as well as new features that can be provided using DWT.

Tables at a glance
Table icon Table icon
Table 1 Table 2

References