Research and Reviews - International Journals

International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Menu

ISSN ONLINE(2278-8875) PRINT (2320-3765)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

N-Point P-Parallel Radix-2^K Feed forward FFT Architecture

R. David jerry Steve1, M. Mohamed rabik2
  1. PG Student [VLSI], Dept. of ECE, NPR College of Engineering and Technology, Natham, Tamilnadu, India
  2. Assistant professor, Dept. of ECE, NPR College of Engineering and Technology, Natham, Tamilnadu, India
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Abstract

The appearance of radix-2^2 was a milestone in the design of pipelined FFT hardware architectures. Later, radix-2^2 was extended to radix-2^k. However, radix-2^k was only proposed for singlepath delay feedback (SDF) architectures, but not for feed-forward ones which is also as called multi-path delay commutator (MDC). This paper presents the radix-2^k feedforward (MDC) FFT architectures. In feedforward architectures, radix-2^k can be used for any number of parallel samples which is a power of two. Furthermore, both decimation in frequency (DIF) and decimation in time (DIT) decompositions can be used. In addition to this, the designs can achieve very high throughputs, which make them suitable for the most demanding applications. Indeed, the proposed radix-2^k feed-forward architectures require fewer hardware resources than parallel feedback ones, also called multi-path delay feedback (MDF), when several samples in parallel must be processed. As a result, the proposed radix-2^k feedforward architectures not only offer an attractive solution for current applications, but also open up a new research line on feedforward structures.





INTRODUCTION
In the present technologies, since the throughput required is in the order of giga samples per second, there arises a need for pipelining, parallelism and efficient FFT architectures. Pipelined architectures were widely used in order to achieve high throughput and low latency along with low area and low power consumption.
Pipelined architecture is of two types. They are feedback architecture and feed forward architecture. Feedback architectures are characterized by their feedback loops. In feedback architecture, some outputs of butterflies will be fed back as inputs to the same butterfly. Feedback architecture is of two types. They are single path delay feedback architecture and multi path delay feedback architecture. Single path delay feedback architecture processes continuous flow of one sample per clock cycle whereas multi path delay feedback architecture or parallel feedback architecture processes several samples in parallel.
Feed forward architecture, also called as multi-path delay commutator (MDC) does not have feedback loops. It processes data and sends them to successive stages. It can process several samples in parallel. At present, in real time applications, high throughput in order of giga samples per second is required in applications such as ultra wide band (UWB) and Orthogonal frequency division multiplexing (OFDM). In real time applications, there are two main challenges. First one is to calculate the fast fourier transform(FFT) of multiple input data sequences arriving one after other. Second challenge is to calculate the fast fourier transform (FFT) when several samples of the same sequence are received in parallel. The second challenge comes into picture when the required throughput is higher than the clock frequency. Both the challenges are effectively met by the feedforward FFT architecture with low area. . Radix-2^k feedforward architecture can take any number of parallel samples to the power of 2.The proposed architecture is more efficient in terms of hardware and performance than parallel feedback designs. Hence, it emerges as an attractive solution for the most demanding applications.

FEEDFORWARD FFT ARCHITECTURE

RADIX-2^2 FFT ALGORITHM
N-point discrete fourier transform of input sequence x(n) is defined as
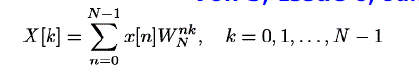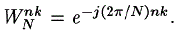image
image
Where, the number of elements N in input sequence is a power of two.
Cooley tukey algorithm on discrete fourier transform, also called as Fast fourier transform reduces the number of operations from O(N^2) in discrete fourier transform to O(N*logN(base2)) in fast fourier transform. Cooley tukey algorithm consists of n= log(N)base(p) stages where p is the base of radix–r of FFT.
Radix-2^2 FFT algorithm takes advantage by breaking down the angles at odd stages into trivial land non trivial rotation ω” and passing the non-trivial rotation to the following even stage.
At odd stages, the breaking down of angle follows the following algorithm. If(ω>N/4) then
ω (stage) = N/4 else
ω (stage) = 0
end if
The non-trivial rotation ω” which will be passed and summed up with rotation of the successive stage is given by
ω” = ω mod N/4.
Therefore at even stages, the rotation angle will be
ω (stage) = ω (stage) + ω”
Simplification is expressed in equation format as
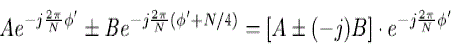image

ANALYSIS OF RADIX-2^2 FLOW GRAPH
The above properties are derived from the radix-2^2 flow graph. These properties are the requirements that any radix-2^2 FFT hardware architecture must fulfill. Properties mainly depend on the index of the data(binary).

RADIX-2^2 FEEDFORWARD FFT ARCHITECTURE
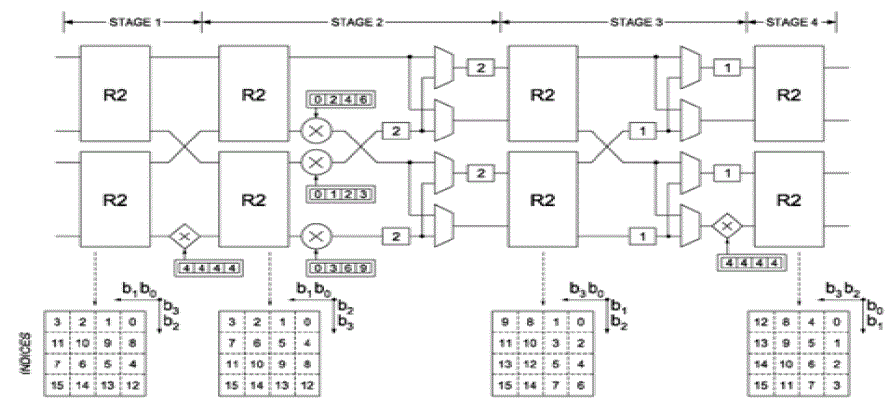
The above diagram shows 4-parellel radix -2^2 feedforward architecture for decimation in frequency fast fourier transform (DIF-FFT). This architecture processes 4 samples in parallel and can process the multiple input sequences one after other to give the outputs. The order of the data shown at the bottom of each stage represents the order of the data in which the data should be fed. The input should be given in the proper order as mentioned in the diagram and the output will be obtained in the order mentioned in the diagram.
An important advantage of feedforward FFT architecture is 100% butterfly utilisation ratio. So it needs less number of butterflies which means low area and low power.

RADIX-2^K FEEDFORWARD FFT ARCHITECTURE
In Radix-2^k feedforward architecture, there are three possible rotations. They are trivial rotations, non-trivial rotations and general rotations.
Trivial rotations are rotations for which the value of ω is either 0 or N/4 or N/2 or 3N/4 i.e. the samples must be rotated by either 0 or 270 or 180 or 90 degrees. They are called trivial because these rotations can be done by interchanging the real and imaginary parts and/or changing the sign of them. So, complex multiplication can be avoided in implementing such rotations. Trivial rotation will be done at odd stages alone.
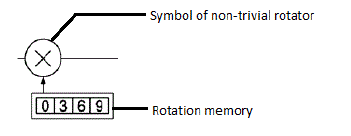
Non trivial rotations will be done only in even stages. In general, for higher values of „k” in radix-2^k feedforward architecture, the non-trivial rotations can be simplified into rotations by W(8) and W(16), which include reduced set of angles, and general rotations for remaining angles. These rotations by W(8) and W(16) can be simplified by the use of trigonometric identities, scaling of coefficients and representation of the coefficients in canonical signed digit (CSD). Rotations by W(8) consider only the angles of π/4. Rotations by W(16) consider only the angles of π/8. For Radix-2^k feedforward FFT architecture, the type of rotation repeats every k stages. For example, radix 2^3 feedforward architecture requires non-trivial rotation every three stages.

SPECIFICATIONS
The specifications of any P-parallel N-point radix-2^k feedforward architecture are shown below.
Number of parallel samples = P = 2^p
Number of butterflies = (P/2) * log N(base 2) = P * log N(base 4)
Number of complex adders = 2 * P * log N(base 4) = P * log N(base 2)
Number of rotators = ((3 * P)/4) * (log N(base 4) – 1) for P > 2
2 * (log N(base 4) – 1) for P = 2
Throughput is the number of output samples obtained in unit time.
Throughput per clock cycle = P = Number of parallel samples
Latency is the time duration between the first input applied and the first output obtained i.e. it mentions the time taken by the system to process an input to give the respective output.
In the proposed architecture, latency = N / P
At any stage„s”,
Length of the buffer in shuffling structure L = N / 2^(s+1)
Total sample memory needed = N – P
Maximum memory needed to perform input reordering along with FFT = N – (N / P)
Maximum memory needed to perform output reordering along with FFT = N
Maximum memory needed to perform both input reordering and output reordering along with FFT = N
Where,
N is the number of inputs in a single sequence
P is the number of parallel input samples in the present stage of operation
Some other facts about feedforward architecture are
1. Memory size will be same for any number of parallel samples.
2. Both DIF FFT and DIT FFT require same number of hardware components
3. Maximum memory needed is N, where N is the number of samples in an input sequence.
4. Most suitable architecture will be selected based on the throughput and latency requirements of the required applications.

IMPLEMENTATION

COMPONENTS

RADIX-2 BUTTERFLY
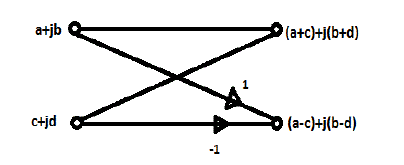
The two inputs to the butterfly always differ in their rotation angle either by 0 or by N/4. Also at any stage„s”, the two inputs which have indices differing only in the bit b(n-s) will be processed together in a butterfly.

TRIVIAL ROTATION
Here the trivial rotation occurs only by N/4 i.e. complex multiplication by (-j). The basic operation of trivial rotation can be performed by interchanging the real and imaginary components and/or changing the sign of them.

NON-TRIVIAL ROTATION
Non trivial rotations will be done only in even stages. In decimation in frequency fast fourier transform, the inputs with indices that satisfies b(n-s+1)+b(n-s)=1 will alone undergo non trivial rotation whereas in decimation in time fast fourier transform, the inputs with indices that satisfies b(n-s-1)+b(n-s-2)=1 will alone undergo non trivial rotation.

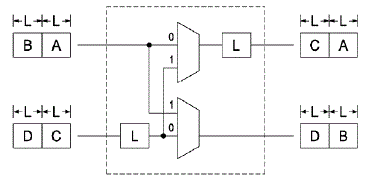
DATA SHUFFLER
Data shuffler consists of two components. They are buffers and multiplexers. In the diagram below, L denotes the length of the buffer. For first L clock cycles, the multiplexer’s selection line will be set to 0. Then for next L clock cycles, the selection line will be set to 1 and the change will happen simultaneously for every L clock cycles.
In the above diagram, for first L clock cycles, A will be stored in output buffer and C will be stored in input buffer. For the consecutive L clock cycles, multiplexer’s select lines will be set to 1. So, B will be directly sent to the lower output. The value A from the output buffer will be sent to the upper output. The value C will be moved from input buffer to output buffer. The value D will be moved to the input buffer. Finally in output, A and B will be available in the second clock cycle and C and D will be available in the next clock cycle. Thus, the inputs are shuffled to get the desired order. The value of L is always a power of two. The control signals of the multiplexer can be directly obtained from the bits of a counter.

VHDL CODE
VHDL language is chosen for programming since it supports lot of loop operations and real operands. The programming was done as a basic FSM (finite state machine) model. Initially, the entire circuit was divided into seven blocks. Each individual block is checked for proper working and then, the blocks are grouped gradually in FSM model and they are checked and errors and logical mistakes were rectified. Then, the output was obtained for a single sixteen point input sequence with a latency of nineteen.
Then, the blocks are combined in order to attain the theoretical latency i.e. latency = N/P = 4. It was observed that each stage in FSM model takes one clock cycle for execution. So, it was concluded that the theoretical latency (in this case, latency = 4) can be obtained only by reducing the entire circuit into a single block.

ONGOING WORK ON DATA TYPE AND ROTATIONS`
The entire model is implemented in Xilinx 9.2i using real data type. But, the real data type can’t be synthesized and hence netlist can’t be created. So, the change of data type from real to Q(m.n) format is being done. Q(22.10) is selected in order to provide maximum accuracy. The two works to be done are, first a synthesized netlist is to be obtained by implementing the code using Q(22.10) format and number of adders multipliers and memory are to be analysed. The second one is to reduce non trivial rotations using different properties and thereby further reducing the number of components needed to implement the architecture.

CONCLUSION
Feedforward architecture saves more area than other architectures as N become larger. Also, feedforward architecture is more efficient than parallel feedback architectures when several samples are processed in parallel. The proposed design also achieves high throughput. Therefore, it is efficient in terms of both area and performance. Another advantage of the proposed architecture is that, the utilization ratio of the butterflies is 100%. So, no part of architecture remains idle thereby performing the operation faster and reduce the power consumption and it requires less number of components since it achieves 100% utilization ratio. Using this proposed architecture, it is possible to attain the throughput in order of giga samples per second at very low latencies.

ACKNOWLEDGEMENT
First, I want to thank god for his abundant grace which sustained me throughout the project. I want to thank my parents who supported me with patience and encouragement. I want to thank my project guide Mr. M. Mohamed Rabik, Asst.Professor of ECE department who has been supporting me with valuable guidance. I also want to thank other staff members and friends who encourage me on this work.

Tables at a glance
Table icon
Table 1

Figures at a glance
Figure Figure Figure Figure
Figure 1 Figure 2 Figure 3 Figure 4
Figure Figure Figure
Figure 5 Figure 6 Figure 7

References