International Journal of Innovative Research in Science, Engineering and Technology

International Journal of Innovative Research in Science, Engineering and Technology

Menu

ISSN ONLINE(2319-8753)PRINT(2347-6710)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

NUMERICAL ANALYSIS of PULSE TUBE CRYOCOOLER

Pravin Mane1, Ashutosh Dasare2, Ganesh Deshmukh3, Pratik Bhuyar4, Kshiteej Deshmukh5, Aditya Barve6
 Assistant Professor, Mechanical Engineering Dept, Walchand College of Engineering, Sangli, Maharashtra, India1
Final year B.Tech Student, Mechanical Engineering Dept, Walchand College of Engineering, Sangli, Maharashtra, India2
Final year B.Tech Student, Mechanical Engineering Dept, Walchand College of Engineering, Sangli, Maharashtra, India3
Final year B.Tech Student, Mechanical Engineering Dept, Walchand College of Engineering, Sangli, Maharashtra, India4
Final year B.Tech Student, Mechanical Engineering Dept, Walchand College of Engineering, Sangli, Maharashtra,India5
Final year B.Tech Student, Mechanical Engineering Dept, Walchand College of Engineering, Sangli, Maharashtra,India6
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology

International Journal of Innovative Research in Science, Engineering and Technology

Abstract

A commercial computational fluid dynamics (CFD) package is used for numerical analysis of the oscillating fluid flow in a pulse tube cryocooler. This model uses helium as a working medium to achieve temperatures in cryogenic range by employing two pulse tubes with 180⁰ phase difference in the mass flow rate and the pressure at the cold end heat exchanger. The cryocooler comprises of compressor, after cooler, regenerator, pulse tube with cold and hot heat exchanger and the inertance tube. A two-dimensional axis symmetric model was used for simulation. This simulation demonstrates the variation in temperature and pressure with respect to time at the cold heat exchanger.

Keywords
pulse tube, cryocooler, CFD, phase difference.
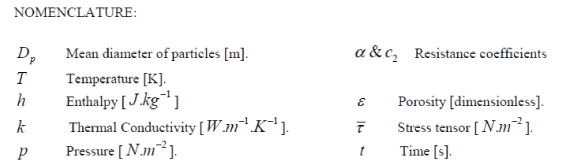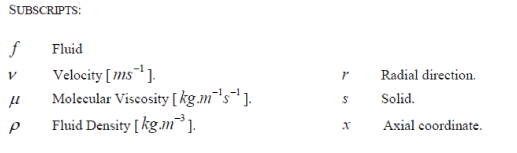image
image

INTRODUCTION
Cryogenics is the branch of physics that deals with the production and study of effects at very low temperatures. Cryogenic Engineering is concerned with temperatures in the range of 0 to 123 K.
The refrigerating machines which are able to achieve and to maintain cryogenic temperature i.e. temperature below 123K are known as cryocoolers. These cryocoolers find applications in space, military and low temperature research as well as in agriculture, transportation and security.
An increased need of cryogenic temperatures in research and huge technological growth during last decade caused a rapid development of cryocoolers. All these applications mostly require efficiency and reliability of the refrigerators along with low cost and long life time. Stirling refrigerators which are primarily used for these cryogenic applications satisfy the above requirements. But the basic problem of these refrigerators is that they have a mean failure time of 4000 hours. This is the reason why they can’t be used in satellites and most of the commercial applications. That is why most of the developments in Stirling refrigerators are concentrated towards the techniques that can improve their reliability. This reliability problem can be overcome by research and development of “Pulse Tube Refrigerators” which are having potential for improved reliability, simplicity and low cost.

II.SIMULATED SYSTEM
The proposed model is the modification of Gawali et.al model in which the orifice is replaced with an inertance tube, as shown in figure. It is called as “Inertance Pulse Tube Refrigerator (IPTR)”. This enables us to eliminate the orifice required in basic Orifice pulse tube refrigerator (OPTR).
In each refrigerator, the volume of gas in pulse tube can be divided into three parts:
1. Cold part: This is the leftmost part of the pulse tube. Here the gas flows from regenerator and expands to give out work.
2. Hot part: This is the rightmost part of the pulse tube. Here the gas flows from the inertance tube and absorbs work. .
3. Middle part: The gas at the centre of the pulse tube never flows out of the pulse tube and is similar to a displacer in a Stirling refrigerator
The solid displacer of the Stirling cycle is replaced by gas displacer. Each refrigerator consists of two heat exchangers namely CHX i.e. cold heat exchanger through which cooling effect is utilized, and HHX i.e. hot heat exchanger for rejection of heat to cooling media.
A. DIMENSIONS OF THE SIMULATED SYSTEM
B. BOUNDARY CONDITIONS
The components are subjected to various boundary conditions as listed in the following table.
C. MATERIALS OF COMPONENTS
We have used FLUENT 6.3.26 as a solver for the analysis in which we have specified the following materials for the corresponding parts.

III.CFD ANALYSIS
A. MESHING IN GAMBIT
The accuracy of analysis of thermo-fluidic problem or system in CFD is strongly depending on the computational mesh structure applied. Meshing is one of the most time consuming processes in pre-processing. Gambit has different features of meshing. The meshing involves discretization of domain into sub domains or cells. These divided domains are used in the numerical solutions of the differential conservation equations of the mathematical model. For meshing different elements and structures quadrilateral and triangular mesh structure is used.
B. CFD MODELLING
The CFD code FLUENT (6.3.26) is used for simulation. The IPTR system is simulated by assuming cylindrical and linear alignment, axis-symmetric, two-dimensional flow, with working media helium as ideal gas. The transient analysis is done because the process is time dependant. Different algorithms, namely SIMPLE, SIMPLEC, PISO and COUPLED are incorporated in commercial CFD Software, and these algorithms are having their own advantages and disadvantages. PISO algorithm has been used in this analysis of the pulse tube refrigerator. PISO algorithm is recommended for unsteady calculations and may sometimes be preferred for steady-state ones. Compressor is modelled by using dynamic mesh feature of the FLUENT. The frequency of the compressor is 12 Hz. The dynamic mesh model in fluent is used to model flows where the shape of the domain is changing with time due to motion of the domain boundaries. The motion is prescribed motion by specifying the linear and angular velocities about the centre of gravity of solid body with time. In order to model compressor, a user defined function with necessary modification was developed in C programming to simulate the piston cylinder effect. Regenerator, Warm Heat Exchanger (WHX), and Cold Heat Exchanger (CHX) were modelled as porous media. Stainless steel wire mesh screens (mesh size 250) were selected as the regenerator packing material, since they offer high heat transfer surface areas, high heat capacity, and low thermal conductivity. Copper mesh (mesh size 150) is used for WHX and CHX. Quadrilateral and triangular mesh structure is used for meshing the IPTR system with different features of Gambit [19]. Total numbers of cells for the model with zero thickness are 32744. Continuum based conservation equation is applied in the system. The mass, momentum and energy equations solved by FLUENT are as follows:
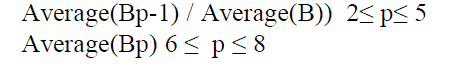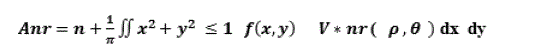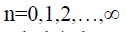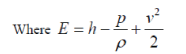image
image
image
image
All properties represent the properties of the working fluid helium. The above equations apply to all components, except for CHX, WHX and the regenerator. The latter three components are modelled as porous media, assuming that within the volume containing the distributed resistance, there exists everywhere local balance between pressure and resistance forces [18].
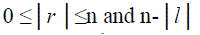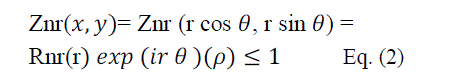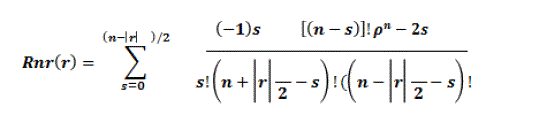image
image
image
All the simulations are carried out as transient processes, starting with an initial system temperature of 300 K. Simulations can be continued until steady-periodic state is obtained. The criterion for steady periodic condition is that the cycle-average temperature of the cold end heat exchanger (CHX) would reach a steady state.
C. ASSUMPTION MADE FOR THE ANALYSIS
1. All components have circular cross-section and have linear alignment.
2. Axis-symmetric geometry is considered for the analysis.
3. Flow is two dimensional and compressible.
4. Helium gas obeys the ideal gas equation.
On the basis of assumption made, the geometry is simplified from three- dimensional to two-dimensional axis symmetric. The property variation in the third direction is strongly dependant on the geometry for the present model and thus is negligible. This simplification will lead to minimum number of cells for meshing and reduce computer time for calculation.

IV.RESULTS AND DISCUSSION
Temperature variation along axial direction is shown in Figure2. Temperature contour along axial direction is shown in Figure3. Significant temperature gradients are predicted in the regenerator and pulse tube.
A. COOL DOWN CHARACTERISTICS
The variation in cycle average temperature at CHX with time is shown in Figure 4.Temperature (cycle average) of 131.994 K is attained after 172.53 sec.
B. PHASE SHIFT
The variation in pressure and mass flow rate with crank angle at CHX is shown Figure 5. The phase difference in pressure and mass flow rate of 400 is observed. The mass flow rate is lagging the pressure wave.
The trends are predicted with the help of CFD tool fluent i.e. figure 2, 3, 4, 5, 6, 7.

V.CONCLUSION
The entire IPTR system operating in periodic state under the given boundary conditions is numerically simulated using CFD code. From present analysis, the lowest temperature at the cold heat exchanger obtained is 132 K in 172 seconds by using helium as the working fluid. The phase shift between the mass flow rate and pressure variation at the cold heat exchanger is observed to be 400. This indicates the feasibility of the use of commercial CFD software packages for analysing the complex fluid flow and heat transfer phenomena that occur in a pulse tube cryocooler.

Tables at a glance
Table icon Table icon Table icon Table icon
Table 1 Table 2 Table 3 Table 4
 

Figures at a glance
Figure 1 Figure 2 Figure 3 Figure 4
Figure 1 Figure 2 Figure 3 Figure 4


Figure 5 Figure 6 Figure 7
Figure 5 Figure 6 Figure 7
 

References
  1. Gifford W. E. and Longsworth, Pulse tube refrigeration progress. Advances in Cryogenic Engineering, Vol. 10, pp. 69-79, (1963).
  2. Gifford W. E. and Longsworth R. C., Pulse tube refrigeration. ASME paper, No. 63-WA 290, (1963).
  3. Mikulin E. I., Tarasov A. A. and Shkrebyonock, Low temperature expansion Pulse Tube. Advances in Cryogenic Engineering, Vol. 29, pp. 629- 637, Plenum press, New York, (1984).
  4. Zhu S.W and Chan Z.Q, “Isothermal model of pulse tube refrigerator”, Cryogenics (1994) Vol.34 PP591-595.
  5. Atrey M.D and Narayankhedkar K.G, “Development of second order isothermal model of orifice type pulse tube refrigerator (OPTR) with linear compressor”, proc, ICEC-18, PP-519-522 (2000).
  6. Gawali B.S., Atrey M.D. and Narayankhedkar K.G. “Performance Prediction and Experimental Investigation of Orifices Pulse Tube Refrigerator” ICEC 19, 2003,pp 391-394.
  7. M.E. Will, A.T.A.M. de Waele. “Analytical treatment of counter flow pulse tube refrigerators” Cryogenics 46 (2006) pp 421-431.
  8. Barrett Flake and ArsalanRazani “Modeling Pulse Tube Cryocoolers With CFD”, Advance Cryogenic Engineering Vol.49 (2004).
  9. J.S. Cha, S.M. Ghiaasiaan, P.V. Desai, J.P. Harvey, C.S. Kirkonnell “ Multi-dimensional Flow Effects in Pulse Tube Refrigerator” Cryogenics 46 (2006) pp 658- 665.
  10. Narayankhedkar K.G. and Gawali B.S. “Design and Development of an Orifice/ Inertance Pulse Tube Cryocooler using a Linear Compressor” CEC 49, pp 1380-1387.
  11. Gawali B.S. and Narayankhedkar K.G. “Performance Prediction and Experimental Investigation to Study the Effect of Hot End Heat Exchanger Volume on Orifice Pulse Tube Cyocooler” ICEC 19, 2003, pp 500-504.
  12. Lothar O. Schunk, John M. Pfotenhauer, Gregory F. Nellis, Ray Radebaugh, E. Luo. “Inertance Tube Optimization for KW- Class Pulse Tubes” Cryogenics 46 pp 200-207.
  13. Xiao-bin Zhang, Zhi-huaGan, Li-min Qiu, Hua-xiang Liu. “Computational Fluid Dynamics Simulation of an Inter-phasing Pulse Tube Cooler” Journal of Zhejiang University Science A 2008 9(1) pp 93-98.
  14. Gawali B.S., Khare S.B., “Theoretical Prediction and Experimental Investigation of Counter Flow Pulse Tube Refrigerator” Indian Journal of Cryogenics Vol. (32) pp 49-53 (2007).
  15. Biredar S.B., Gawali B.S., “Analysis of Inertance Pulse Tube Cryocooler using Computational Fluid Dynamics” Indian Journal of Cryogenics Vol. (32) pp 41-45 (2007).
  16. Anarase R.N. and Gawali B.S. “Analysis of counter flow heat exchanger used in pulse tube refrigerator” IJC 2008, pp 230-236.
  17. Gawali B.S. and Mane P.A. “CFD study of orifice pulse tube cryocoolers” IJC 2010, pp 538-543.
  18. Fluent 6.3.26 Users guide, Fluent. Inc.
  19. Gambit 2.3.16 Users guide.