International Journal of Innovative Research in Science, Engineering and Technology
MenuISSN ONLINE(2319-8753)PRINT(2347-6710)
ISSN ONLINE(2319-8753)PRINT(2347-6710)
R.LAKSHMI1, M.MUTHUSELVI2
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology
In this paper, Numerical Methods for solving ordinary differential equations, beginning with basic techniques of finite difference methods for linear boundary value problem is investigated. Numerical solution is found for the boundary value problem using finite difference method and the results are compared with analytical solution. MATLAB coding is developed for the finite difference method. The results are reported for conclusion.
Keywords |
| Ordinary Differential Equations, finite Difference method, Boundary value problem, Analytical solution, Numerical solution |
INTRODUCTION |
| In mathematics, finite-difference methods are numerical methods for approximating the solutions to differential equations using finite difference equations to approximate derivatives. Finite differences method is used in soil physics problems. An important application of finite differences is in numerical analysis, especially in numerical differential equations, which aim at the numerical solution of ordinary and partial differential equations respectively. The idea is to replace the derivatives appearing in the differential equation by finite differences that approximate them. The resulting methods are called finite difference methods. Common applications of the finite difference method are in computational science and engineering disciplines, such as thermal engineering, fluid mechanics, etc. |
| A. STEPS INVOLVED IN FINITE DIFFERENCE METHOD |
| A finite difference method typically involves the following steps: Generate a grid, for example (xt ; t (k)), where we want to find an approximate solution. |
| Substitute the derivatives in a system of ordinary differential equations with finite difference schemes. |
| The ordinary differential equation then becomes a linear/non-linear system of algebraic equations. |
| Solve the system of algebraic equations. Implement and debug the computer code. |
| Do the error analysis, both analytically and numerically. |
| B. DERIVATION OF FINITE DIFFERENCE METHOD |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
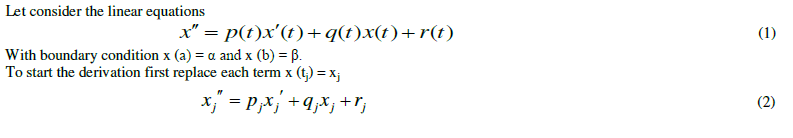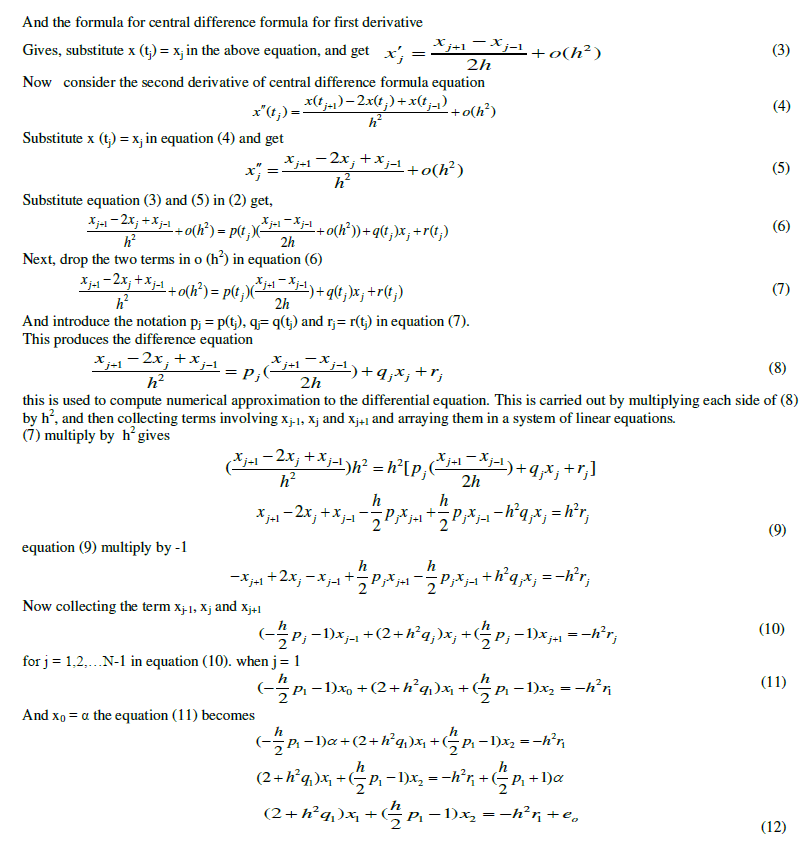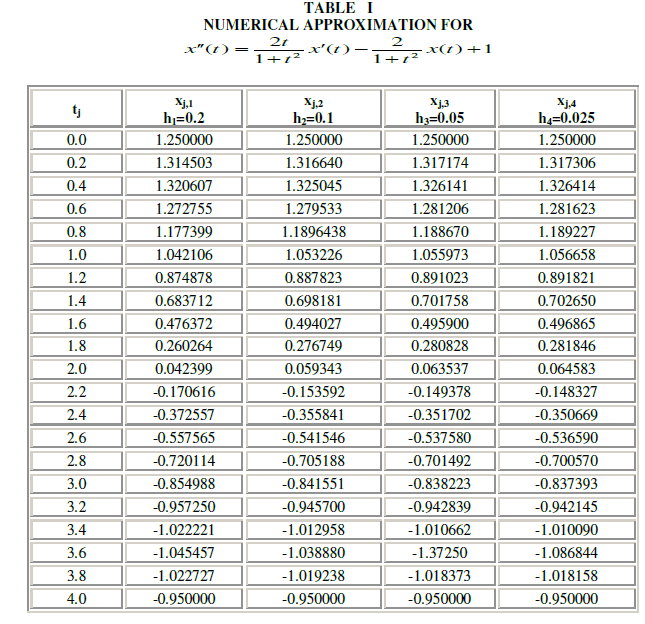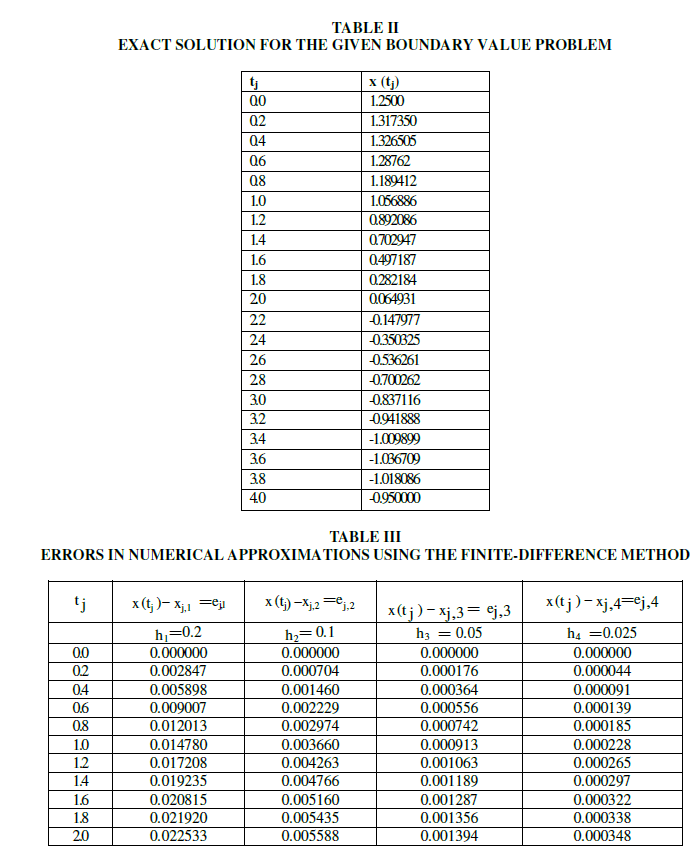CONCLUSION |
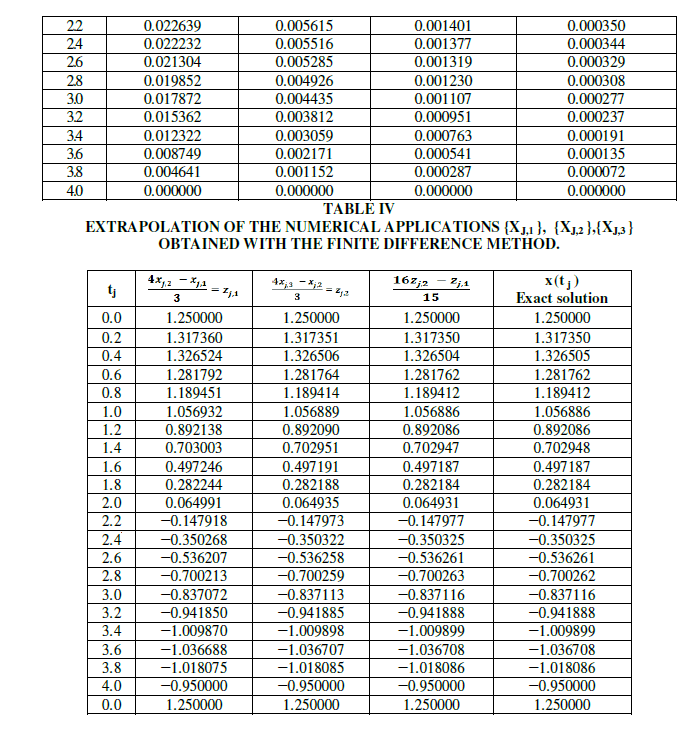
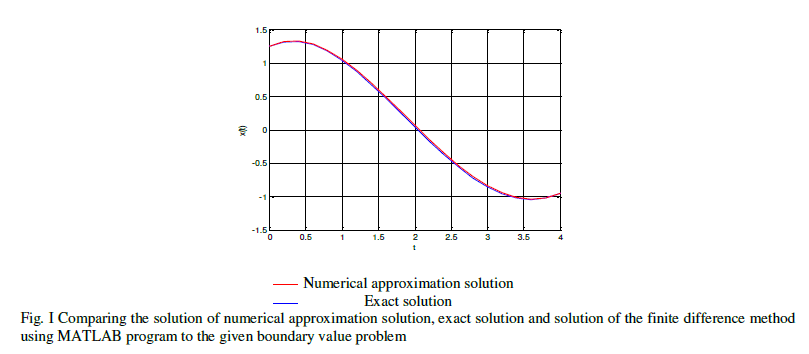
| A boundary value problem is solved using finite difference method and is verified with exact solution. It is found that the results are agreed with exact solution. |
References |
|