Numerical Solution of a Linear Black-Scholes Model: A Comparative Overview

Abstract

Black-Scholes equation is a well-known partial differential equation in financial mathematics. In this paper we try to solve the European options (Call and Put) using different numerical methods as well as analytical methods. We approximate the model using a Finite Element Method (FEM) followed by weighted average method using different weights for numerical approximations. We present the numerical result of semidiscrete and full discrete schemes for European Call option and Put option by Finite Difference Method and Finite Element Method. We also present the difference of these two methods. Finally, we investigate some linear algebra solvers to verify the superiority of the solvers.

Keywords

Black-Scholes model; Call and put options; Exact solution; Finite difference schemes, Finite Element Methods

Introduction

A powerful tool for valuation of equity options is the Black-Scholes mode [1,2]. This model is used for finding the prices of stocks. Company et al. [3] solved the modified Black-Scholes equation pricing option with discrete dividend. A delta-defining sequence of generalized Dirac-Delta function and the Mellin transformation are used toobtain an integral formula. Finally numerical quadrature approximation is used to approximate the solution. In some papers like [4] Mellin transformation is used. They were required neither variable transformation nor solving diffusion equation. Jodar et al. [4] found the solution of BS equation with a wide class of payoff functions that contains not only the Dirac delta type functions but also the ordinary payoff functions with discontinuities of their derivatives. Julia Ankudiova and Matthias Ehrhardt [5] solved nonlinear Black-Scholes equations numerically. They focused on various models relevant with the Black-Scholes equations with volatility depending on several factors. They also worked on the European Call option and American Call option analytically using transformation into convection diffusion equation with nonlinear term and the free boundary problem respectively. In our previous paper [6] we discussed about the analytical solution of Black-Scholes equation using Fourier Transformation method for European options. We formulated the Finite Difference Scheme and find the solutions of them. In this paper we discuss the solution with Finite Element Method and compare the result with the result obtained by Finite Difference Schemes.

Model Equation

The linear Black-Scholes equation [1,2] developed by Fischer Black and Myron Scholes in 1973 is

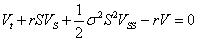(1)

where

V =V (S,t ), the pay − off function

S = S (t ), the stock price, with S = S (t ) ≥ 0,

t = time,

r = Risk − Free interest rate,

σ =Volatility Condition

And also t ∈ (0,T )

where T is time of maturity.

The terminal and boundary conditions [7] for both the European Call and Put options stated below.

European Call Option [7]

The solution to the Black-Scholes equation (1) is the value V (S,t ) of the European Call option on $ 0 ≤ S < ∞ , 0 ≤ t ≤ T . The boundary and terminal conditions are as follows

V (0,t) = 0 for 0 ≤ t ≤ T,

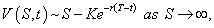(2)

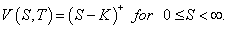
European Put Option [7]

European Put option is the reciprocal of the European Call option and the boundary and terminal conditions are

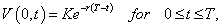
V (S,t )→ 0 as S →∞, (3)

Transformation

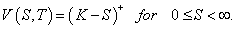
The model problem stated in (1) is a backward type. This type is little bit difficult to solve. To solve the problem in (1) with the conditions stated in (2) and (3) we need to make the model in forward type. In this regard, we have the following transformations.

Let

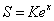
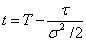
And

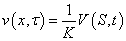
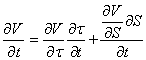
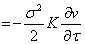
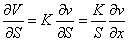
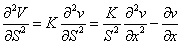
inserting these derivatives in equation (1) we have

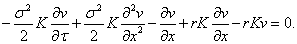
implies

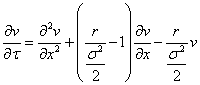(4)

Let

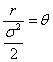
(4) implies

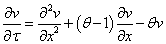
Now let

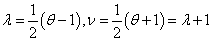
so that

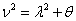
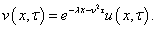
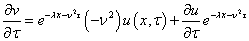
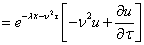
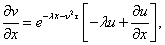
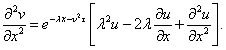
inserting these into equation(5) and dividing by 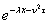we get

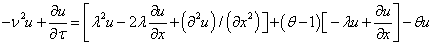
Implies

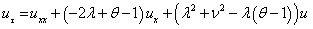
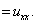
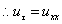
And the initial an boundary conditions for the European Call and Put options are respectively

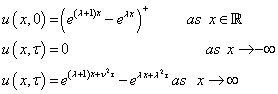(7)

and

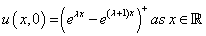
(8)

Thus the Black-Scholes equation reduced to a heat diffusion equation

Numerical Approximation of Transformed Linear Black-Scholes Model

Now we solve the problems numerically. We use the Finite Element Method (FEM) to solve the problems related to the differential equation (6). Finally back substitution of the coordinate transformation gives the solution of the problems related to the differential equation (1).

We have the model

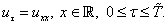(9)

and the initial and boundary conditions for call option are

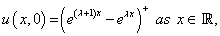
(10)

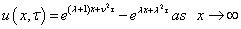
The weak form of the governing equation is

(11)

Discretizing spatially, we have

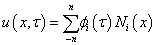(12)

where 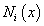are given shape functions, and 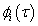are unknown, and n is the ordinal number of nodes.

Substituting (12) into (11), we get the weak semidiscretized equation

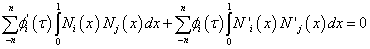(13)

Let 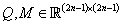denote the so-called mass and stiffness matrices, respectively, defined by:

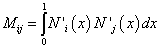(14)

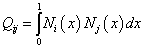(15)

Then (13) can be expressed as:

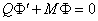(16)

where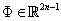 is a vector function with the components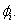

After performing the integral in (14) and (15) for the linear shape functions, the mass and the stiffness matrices have the following form

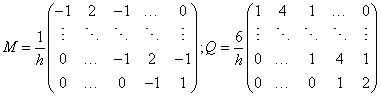
where h is the length of the spatial approximation.

Now we would like to discrete the equation (16) with respect to time. One may start with a simple scheme.

One of the trivial choice is to use the forward Euler scheme. Firstly we discrete (16) explicitly and we have

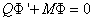
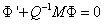
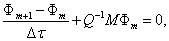
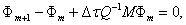
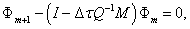
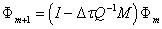
The difficulty of using the scheme is that it needs very little step size to converge , as a result the scheme is a slow one, and is not of interest in this advance study.

We want a fast and efficient scheme, so we want larger time stepping, and interested in using implicit techniques. We dis crete (16) implicitly and have

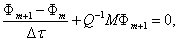
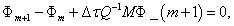
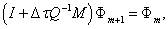
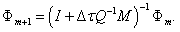(18)

which is a system of linear equations with unknowns 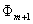. The advantage of using (18)

is that the scheme is unconditionally stable . Equation (18) accuracy of order 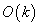. It is faster than the explicit Euler scheme since (18) allows us to use large time steps.

We use an weighted average method to discrete (16) with weight and we have

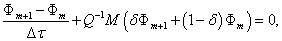
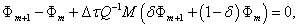
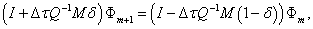
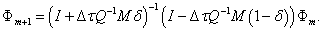(18)

which is a system of linear equations with unknowns 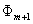. The advantage of using (18)

is that the scheme is unconditionally stable . Equation (18) accuracy of order O(k ) . It is faster than the explicit Euler scheme since (18) allows us to use large time steps.

We use an weighted average method to discrete (16) with weight and 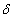we have

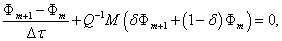
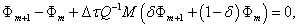
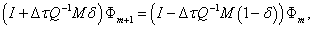
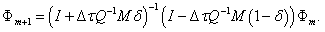(19)

This system is also a linear one with unknowns 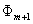where 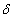varies from 0 to 1. This method turns to the explicit method when 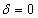i.e., equations (17) and (19) are same and implicit method when 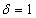,i.e., equations (18) and (19)are same. For 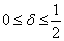the scheme is conditionally stable and unconditionally stable for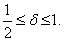

The order of the accuracy of the scheme is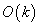

Resultas, Discusión and Conclusión

In this section we have presented the results by various methods. We have solved the model analytically [8] by the method of Fourier Transformation. In Figure 1 we placed the analytic solution of two options (Call Option and Put Option). To solve the model numerically we have applied [8] Finite difference methods (FDM) and have shown the result of the two options in Figure 2. Our interest in this paper was in the methods of Finite Elements (FEM) [9] .Firstly, we have discretized the model (6) spatially in the section (4). Then we have used various one step Euler’s time integrations to discretize the system of linear equations obtained by semi-discretization. The results have been presented in Figure 3. We have tried to show comparison between the methods (FDM and FEM) in Figure 4.

The system of linear equations (19) generated by the discretization of the Black-Scholes model can be solved by many conventional processes. For a large scale linear system, scientists rarely use direct methods as they are computationally costly. Here, in this section, it is our motivation to solve the system of equation (19) using various iterative techniques. Here we first investigate which linear solver converges swiftly. To that end, we consider Jacobi iterative method, Gauss-Seidel iterative method and successive over relaxation method to start with. In terms of matrices, the Jacobi method can be expressed as

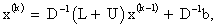
Gauss-Seidel method

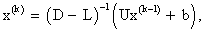
and the SOR algorithm can be written as

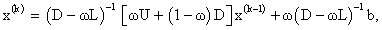
where in each case the matrices D, − L , and −U represent the diagonal, strictly lower triangular, and strictly upper triangular parts of A, respectively.

We investigate Preconditioned Conjugate Gradient (PCG) Method and Generalized Minimal Residual (GMRES) Method with a diagonal preconditioning [10]. Here for all computations we consider 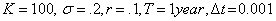. The results are presented with different weights δ. Observing Figure 5, we notice that Preconditioned Conjugate Gradient (PCG) Method performs the best.

References

1. Merton RC. Theory of rational option pricing. Bell J Econ, 1973; 4: 141–183.
2. Black F, Scholes M. The pricing of options and corporate liabilities. J Pol Econ, 1973; 81: 637–659.
3. Company R, GonzalezAL,Jodar L. Numerical solution of modified Black–Scholes equation pricing stock options with discrete dividend, Mathematical and Computer Modeling.2006; 44; 1058–1068.
4. Jodar L, Sevilla-PerisR, CortosJC, Sala R. A new direct method for solving the Black-Scholes equation. Applied Mathematics Letters, 2005; 18: 29–32.
5. Duffy DJ. Finite Difference Methods in Financial Engineering (A Partial Differential Equation Ap-proach). John Wiley & Sons Ltd, The Atrium, Southern Gate, Chichester, England, 2000.
6. Salah Uddin MK, Ahmed M,Bhowmik SK. A Note on Numerical Solution of A Linear Black-Scholes Model. GANIT J Bangladesh Math Soc, 2013;33: 103- 115.
7. Ehrhardt PDM andUnterreiter A. The numerical solution of nonlinear Black–Scholes equations.TechnischeUniversitat Berlin, 2008.
8. Salah Uddin MK, Ahmed M,Bhowmik SK. A Note on Numerical Solution of A Linear Black-Scholes Model. GANIT J Bangladesh Math Soc, 2013;33: 103- 115.
9. Lewis PE and WardJP. The Finite Element Method: Principles and Applications. ADDISONWESLEY PUBLISHING COMPANY.
10. BhowmikSK. Fast and efficient numerical methods for an extended Black-Scholes model. arXiv, 2013.