Department of Mathematics, University of Michigan, Ann Arbor, Michigan, 48109, USA.
Received Date: 01/11/2015; Accepted Date: 04/11/2015; Published Date: 16/11/2015
Visit for more related articles at Research & Reviews: Journal of Statistics and Mathematical Sciences
In this article we will summarize different numerical methods that have been used to study the starting vortex dynamics as fluid flows past a solid body. The fluid motion considered here is Newtonian and incompressible. For a fluid flow in the a limit of zero viscosity, the vortex sheet model can be used; For a viscous flow, both Lagrangian method, such as the vortex method, and Eulerian method, such as the finite difference method, are usually seen in literature.
Vortex separation at the edge of a solid body is a fundamental process in fluid dynamics which finds great applications in life, including the bird flying, fish swimming and ship turbine rotating. As the fluid flow passes around a body, the vorticity boundary layer forms along the body surface and concentrates at the body edge. Such a concentration of vorticity grows thick, separates as a shear layer, giving birth to a starting vortex, which eventually convects downstream. The goal of this article is to provide a summary of various numerical methods that have been used to study the starting vortex. We focus on problems of flow past a flat plate or a thin ellipse.
The fluid flow is assumed to be Newtonian and incompressible, thus the fluid motion is governed by the Navier-Stokes equations,
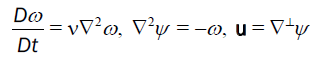. (1)
Here, the fluid vorticity is ω, velocity vector u, stream function ψ, and the kinematic fluid viscosity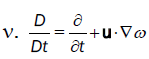 
is the
material derivative, and is usually used to describe the flow motion in the Lagrangian frame. The Reynolds number Re = LU/ν
is a dimensionless parameter that characterizes the physical geometry and properties of the fluid flow. In the case of the plate
(ellipse) L is the plate length (long axis of the ellipse) and U is the far field flow speed.
The pioneering study of starting vortex dynamics dates back to Prandtl [1]. The past several decades have seen significant advance in the numerical simulation of starting vortex dynamics.
Vortex sheet model. Concerning the case of inviscid fluid flow, the vortex sheet model is widely used. The vortex sheet is an asymptotic model of the vorticity boundary layer as the fluid viscosity tends to zero. The sheet is a line with zero thickness and consists of discrete vortices. The mathematical formulation of the vortex sheet has singularities, and inserting an artificial smoothing parameter is a common technique to regularize the problem[2].
Pullin[3] studied the self-similar roll-up of a semi-infinite vortex sheet and shear-layer separations as power-law starting flow past a semi-finite wedge using vortex sheet model. Krasny [4] regularized the vortex sheet and investigated the evolution of the sheet past the critical time. He also applied the regularization technique to study the vortex sheet roll-up in trefftz plane[5]. For the asymmetric case, Nitsche and Krasny [6] simulated vortex ring formation at the edge of a circular tube. Results compared very well with the similarity theory and the experiment, and discrepancies with experiments were attributed to absence of viscosity in the vortex sheet model. Alben[7] applied vortex sheet model to probe the bio-mechanism a flexible body in the inviscid flow, for example, the krill swimming [8]. Huang, Nitsche and Kanso [9] investigated the stability and maneuverability in the insect hovering flight.
Lagrangian method. Viscous vortex method is a Lagrangian method. During the computation, an array of fluid particles are tracked and these fluid particles carry vorticity. The associated velocity and stream function can be calculated via the Biot-Savart law. Fluid particles are absent at the body surface, thus a way to approximate vorticity diffusion at the solid boundary is desired in the numerical process. Schmall and Kinney [10] introduced a technique to diffuse vorticity from the solid boundary to the fluid flow based on the surface adherence condition. They showed vorticity contours around the body at Re = 4 and 400 in the case of an unsteady two-dimensional viscous flow past a finite plate at an angle of attack. Koumoutsakos and Shields [11] employed the same technique to study flow past a flat plate. Eldredge [12] investigated vortex around a flapping 2D rigid elliptic body using vortex method. In his computation, a background Cartesian grid is used to assist the particle remeshing procedure.
Eulerian method. In this category, we will focus on the finite different method. The finite different method approximates the differential operators in the Navier-Stokes equations with difference equations. Solutions of vorticity, velocity and stream function reside on the grid node. In the computation, a body-fitted grid is usually generated so that the solid body profile is a grid line. Therefore Briley’s formula [13] can be applied directly to ensure the no slip and no penetration conditions at the fluid-solid interface. In some cases, the analytic asymptotic solutions are used to treat the singular behavior of the edge tip [14]. Hudson and Dennis [15] investigated the steady-state solutions of fluid past a normal flat plate at low and intermediate Reynolds numbers, Re ∈ [0.1,20]. Wang, et al. [16] connected the secondary instabilities in the starting vortex shear layer with oscillating values of stream functions near an ellipse tip. Xu and Nitsche [17,18] studied viscous flow past a finite plate with varying Reynolds numbers Re ∈ [250,2000] and accelerating flow rate. Parallel computing is employed to obtain high-resolution results near the plate tip, and the scaling behavior of the starting vortex at an early time period is investigated. Nitsche and Xu [19] discussed the comparison between the viscous and inviscid simulations.
Though the inviscid vortex sheet model provides great insight into the fluid separation at sharp edges and large scale structures of the starting vortex, direct simulations of viscous flow get increasing attention these days, largely because they solve the full Navier-Stokes equations and are more realistic in problems where viscosity plays an important role. High performance computing on the other hand assists the advancement of direct simulations. These supercomputers, which in the past were used only by few researchers, have become more and more accessible to graduate students and general researchers. Nevertheless, the design and improvement of better numerical techniques will never stop as the challenges from real-life are endless.
Menu