OBSERVATIONS ON THE NON HOMOGENEOUS EQUATION OF THE EIGHTHDEGREE WITH FIVE UNKNOWNS

Vidhyalakshmi.S; Lakshmi.K; Gopalan.M.A

OBSERVATIONS ON THE NON HOMOGENEOUS EQUATION OF THE EIGHTHDEGREE WITH FIVE UNKNOWNS

Vidhyalakshmi.S1, Lakshmi.K2, Gopalan.M.A3
Professor, Department of Mathematics, SIGC ,Trichy,Tamil nadu, India1
Lecturer, Department of Mathematics,SIGC ,Trichy, Tamil nadu, India2
Professor, Department of Mathematics,SIGC ,Trichy, Tamil nadu, India3

Corresponding Author: SHARMA VIVEK, E-mail: vivek03sharma@rediffmail.com

Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology

Abstract

We obtain infinitely many non-zero integer quintiples (x, y, z,w, p) satisfying the nonhomogeneous equation of degree eight with five unknowns given by 4 4 2 2 2 2 6 x Ã¯Â€Â y Ã¯Â€Â½ (k Ã¯Â€Â« s )(z Ã¯Â€Âw )p .Various interesting relations between the solutions and special numbers, namely, polygonal numbers, Pyramidal numbers, Star numbers, Stella Octangular numbers, Octahedral numbers, Four Dimensional Figurative numbers, Five Dimensional Figurative numbers and six Dimensional Figurative numbers are exhibited.

Keywords

Non-homogeneous equation, integral solutions, 2-dimentional, 3-dimentional, 4- dimensional and 5- dimensional and 6- dimensional figurative numbers.

MSC 2000 Mathematics subject classification: 11D41.

NOTATIONS

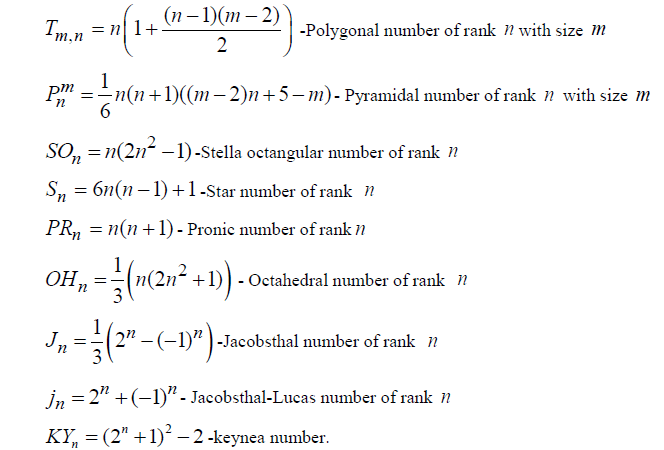INTRODUCTION

The theory of diophantine equations offers a rich variety of fascinating problems. In particular, homogeneous and non-homogeneous equations of higher degree have aroused the interest of numerous mathematicians since antiquity[1- 3]. Particularly in [4, 5] special equations of sixth degree with four and five unknowns are studied. In [6-8] heptic equations with three and five unknowns are analysed. This paper concerns with the problem of determining non-trivial integral solution of the non- homogeneous equation of eighth degree with five unknowns given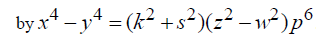

. A few relations between the solutions and the special numbers are presented.

II.METHOD OF ANALYSIS

The Diophantine equation representing the non- homogeneous equation of degree eight under consideration is given by

Introduction of the transformations

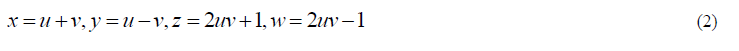in (1) leads to

The above equation (3) is solved through different approaches and thus, one obtains different sets of solutions to (1)

A. Case1:

is not a perfect square

1)Approach1: Let p=a2+b2 (4)

Substituting (4) in (3) and using the method of factorisation, define

Equating real and imaginary parts in (5) we get

where

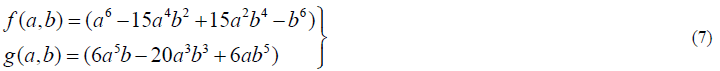In view of (2), (4), (6) and (7), the corresponding values of x, y, z,w and p are represented by

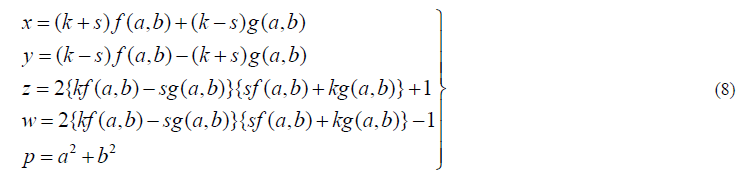The above values of x, y, z,w and p satisfy the following properties:

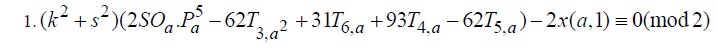2. The following are nasty numbers

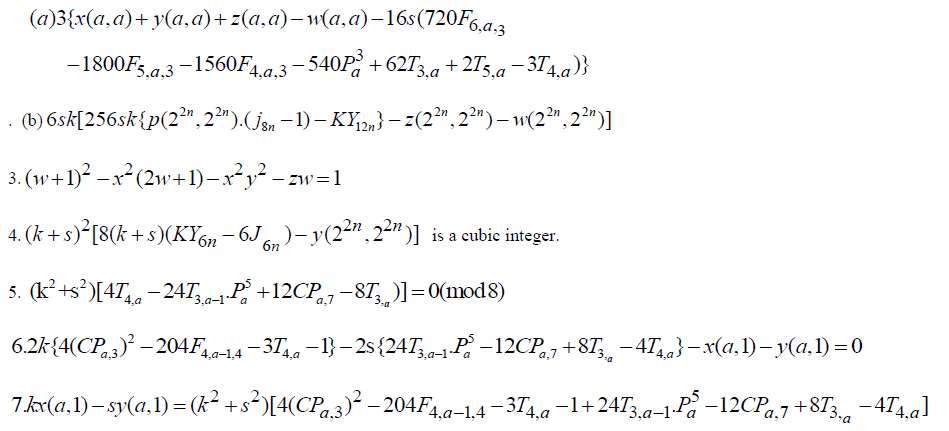2) Remark1: Instead of (2), taking the substitution in (1) as

We get the solution of (1) as

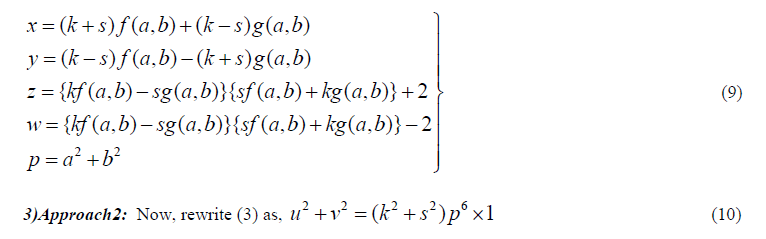Also 1 can be written as 1=(-i)(i) (11)

Substituting (4) and (11) in (10) and using the method of factorisation, define,

Following the same procedure as in approach1 we get the integral solution of (1) as

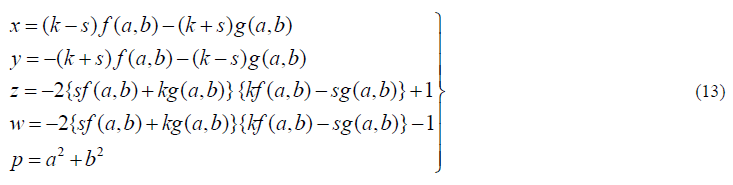4)Approach3:1 can also be written as

Substituting (4) and (14) in (10) and using the method of factorisation, define

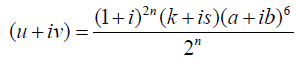Equating real and imaginary parts in (5) we get

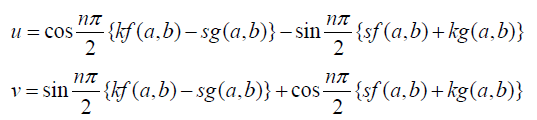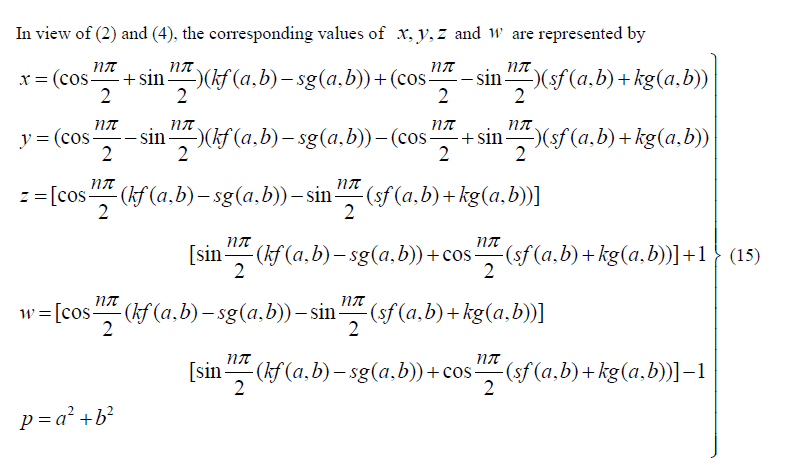5) Approach4: 1 can also be written as

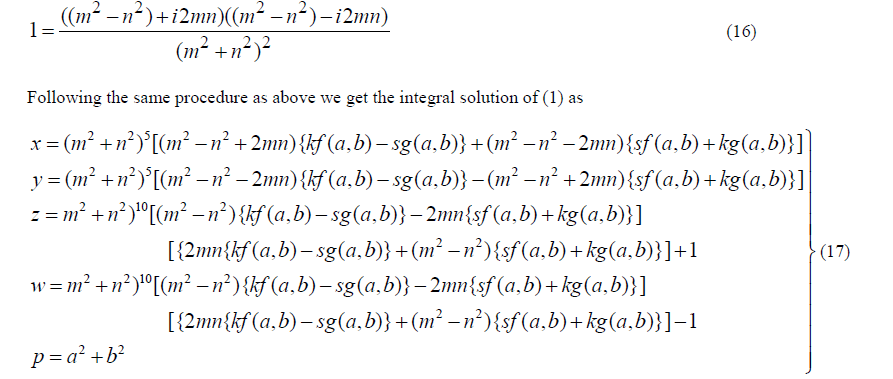6)Approach5: Writing 1 as

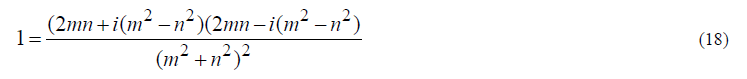Following the same procedure as above we get the integral solution of (1) as

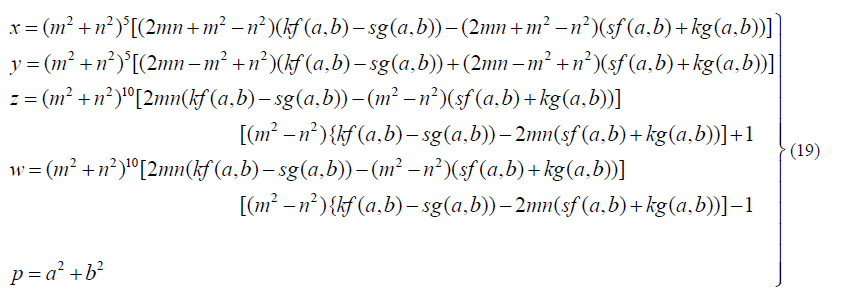7)Approach6:Rewriting (3) as

Let p =α . Using the method of factorisation, writing (20) as a system of double equations,

solving it and using (2), we get the solution of (1) as

B. Case2: k2+s2 is a perfect square

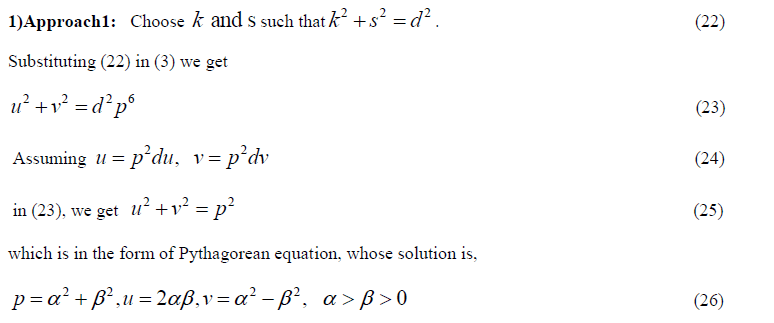Using (24), (26) and (2), we get the integral solution of (1) as

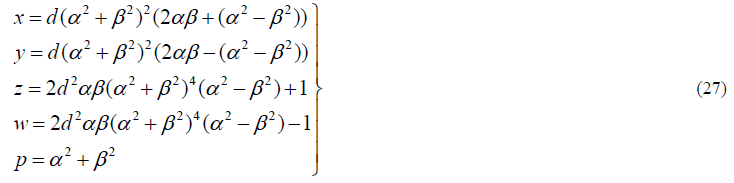It is to be noted that, the solutions of (25) may also be written as

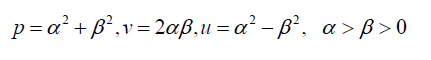Hence we get a different solution of (1) as

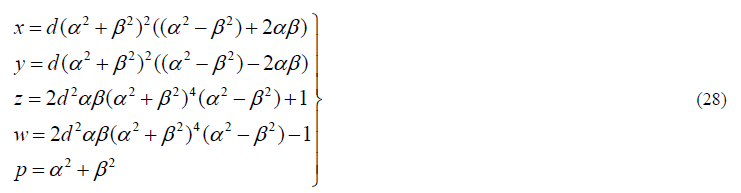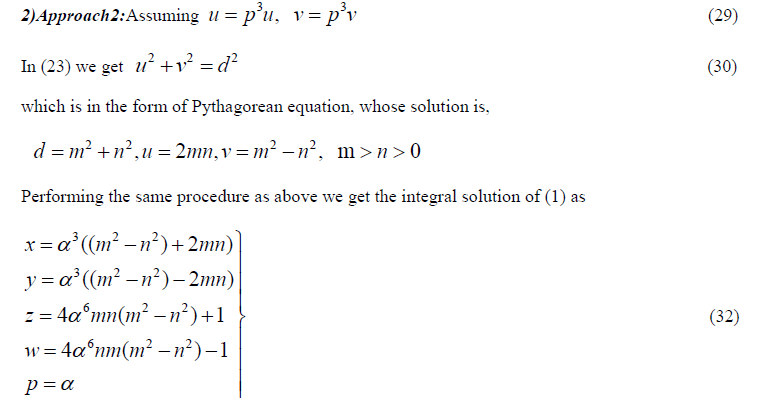It is to be noted that, the solutions of (30) may also be written as

Then we get a different solution to (1)

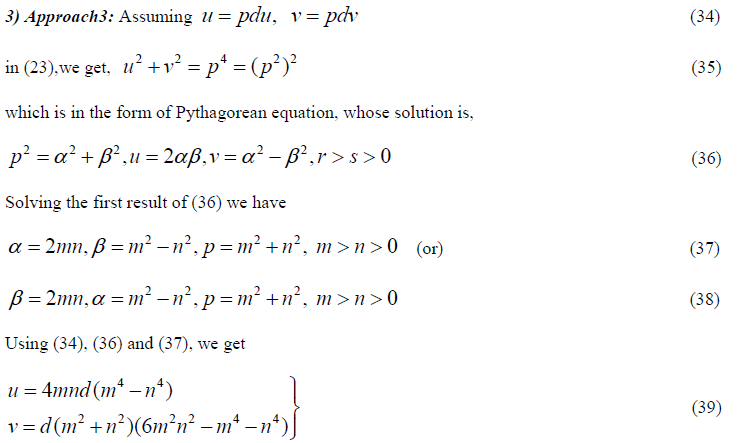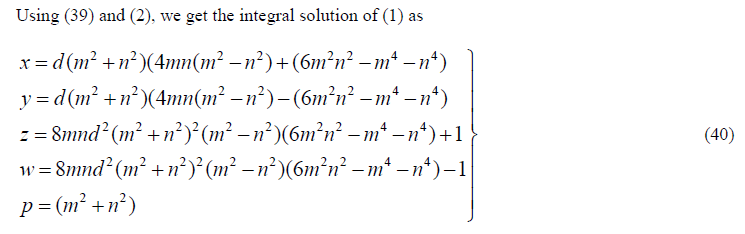Similarly using (34), (36), (38) and (2) we get a distinct solution to (1)

It is to be noted that, the solutions of (35) may also be written as

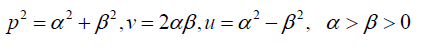Again performing the same procedure as above, we will get two more different integral solutions to (1)

4) Approach4: Also, taking p=m2+n2 (41)

in (35) and applying the method of factorisation define,

Equating real and imaginary parts in (42) we get

Using (34), (41), (43) and (2), we get the integral solution of (1) as

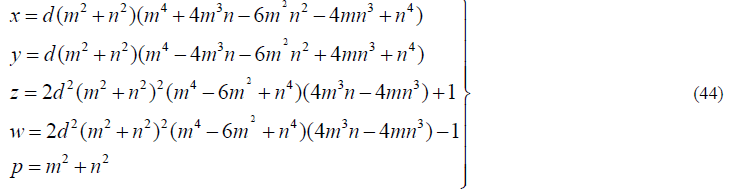By using the same procedure as in approaches 2-5 we get 4 more patterns of solutions to (1)

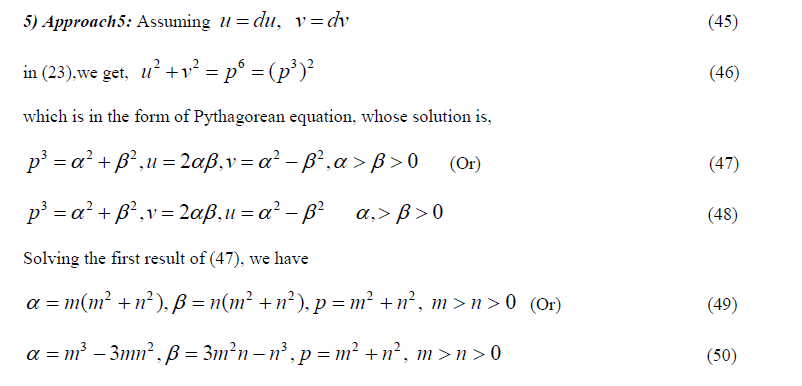In view of (49), (47), (45) and (2), we get the integral solution of (1) as

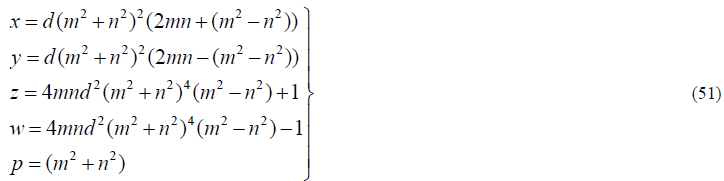In view of (50), (47), (45) and (2), we get a different integral solution of (1) as

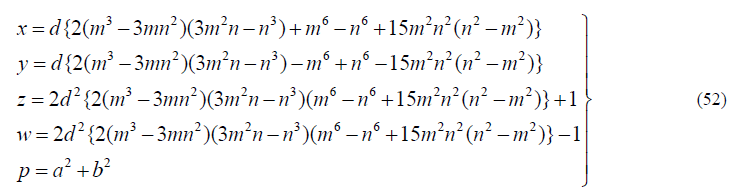6)Remark2: Similarly taking (48) and performing the same procedure we will get two more patterns.

III.CONCLUSION

In conclusion, one may search for different patterns of solutions to (1) and their corresponding properties

References

L.E.Dickson, History of Theory of Numbers, Vol.11, Chelsea Publishing company,New York (1952).
L.J.Mordell, Diophantine equations, Academic Press, London(1969)
Carmichael ,R.D.,The theory of numbers and Diophantine Analysis,Dover Publications, New York (1959)
M.A.Gopalan,S.Vidhyalakshmi and K.Lakshmi, On the non-homogeneous sextic equation ,IJAMA,4(2),171-173,Dec.2012
M.A.Gopalan,S.Vidhyalakshmi and K.Lakshmi, Integral Solutions of the sextic equation with five unknowns , IJESRT, 1(10),502-504,Nov..2012
M.A.Gopalan and sangeetha.G, parametric integral solutions of the heptic equation with 5unknowns ,Bessel Journal of Mathematics 1(1), 17-22, 2011.
M.A.Gopalan and sangeetha.G, On the heptic diophantine equations with 5 unknowns ,Antarctica Journal of Mathematics, 9(5), 371-375, 2012
Manjusomnath, G.sangeetha and M.A.Gopalan, On the non-homogeneous heptic equations with 3 unknowns ,Diophantine journal of Mathematics, 1(2), 117-121, 2012