ISSN ONLINE(2319-8753)PRINT(2347-6710)
ISSN ONLINE(2319-8753)PRINT(2347-6710)
| S.Vidhyalakshmi1, S.Mallika2, M.A.Gopalan3 Assistant Professor of Mathematics , SIGC, Trichy-2,Tamilnadu,India 1 Lecturer of Mathematics , SIGC, Trichy-2,Tamilnadu,India 2 Assistant Professor of Mathematics , SIGC, Trichy-2,Tamilnadu,India3 |
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology
The sextic non-homogeneous equation with four unknowns represented by the Diophantine equation x y k z w 3 3 2 5   2(  3) is analyzed for its patterns of non-zero distinct integral solutions are illustrated. Various interesting relations between the solutions and special numbers, namely polygonal numbers, Pyramidal numbers, Jacobsthal numbers, Jacobsthal-Lucas number, Pronic numbers, Star numbers are exhibited.
Keywords |
| Quintic equation with five unknowns, Integral solutions, centered polygonal numbers, centered pyramidal numbers. |
| Mathematics subject classification number: 11D41. |
NOTATIONS |
 - Polygonal number of rank n with size m. - Polygonal number of rank n with size m. |
 - Pyramidal number of rank n with size m. - Pyramidal number of rank n with size m. |
 - Pentatope number of rank n - Pentatope number of rank n |
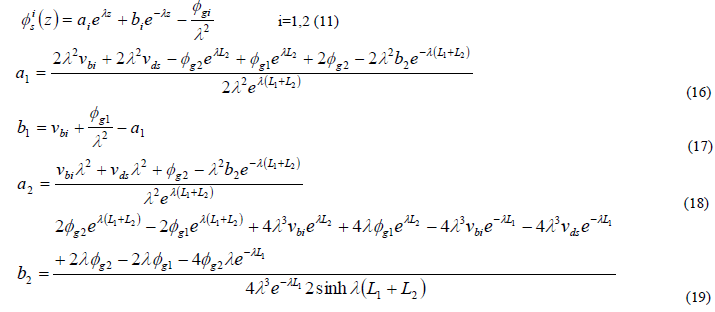 -Stella octangular number of rank n -Stella octangular number of rank n |
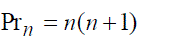 - Pronic number of rank n. - Pronic number of rank n. |
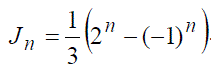 Jacobsthal number of rank n. Jacobsthal number of rank n. |
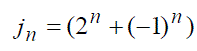 - Jacobsthal lucas number of rank n. - Jacobsthal lucas number of rank n. |
 - Four dimensional figurative number of rank n - Four dimensional figurative number of rank n |
| whose generating polygon is a triangle. |
 -Five dimensional figurative number of rank n whose generating polygon is a triangle. -Five dimensional figurative number of rank n whose generating polygon is a triangle. |
 - Centered polygonal number of rank n with size m. - Centered polygonal number of rank n with size m. |
I.INTRODUCTION |
The theory of Diophantine equations offers a rich variety of fascinating problems. In particular quintic equations homogeneous or non-homogeneous have aroused the interest of numerous mathematicians since antiquity [1,2,3].For illustration ,one may refer [4-10],for quintic equations with three ,four and five unknowns. This paper concerns with the problem of determining integral solutions of the non-homogeneous quintic equation with five unknowns given by  . A few relations between the solutions and the special numbers are presented.. . A few relations between the solutions and the special numbers are presented.. |
II.METHOD OF ANALYSIS |
| The Diophantine equation representing the quintic with five unknowns under consideration is |
 (1) (1) |
| Introducing the transformations |
| where ïÃÂá is a distinct positive distinct integer in (1),we get |
| Assume |
| Substituting (4) in (3) and employing the method of factorization define |
| equating real and imaginary parts, we get |
 |
| Thus, in view of (2), the non-zero distinct integral solutions of (1) are given by |
 |
| For simplicity and clear understanding we present below the integer solutions and the corresponding properties for α 0 and α1. |
| A. Case:1 |
| Let α 0 The non-zero distinct integer solutions of (1) are found to be |
 |
| B.Properties |
 |
| 1) Remark : It is worth to note that when α 0,we have another pattern of solution which is illustrated below. |
| For this case α 0 ,(3) reduces to |
 (6) (6) |
| Following the analysis presented above ,the values of u and v are given by |
 |
| Hence, the non-zero distinct integral solutions of (1) are given by, |
 |
| The above values of x, y, z and w are different from that of in case (1) presented above. |
| C.Properties: |
 |
 |
| D.Case:2 |
| Let α1 .After performing a few calculations as in case (1) the non-zero distinct integer solutions are obtained as |
 |
| E.Properties: |
 |
III.CONCLUSION |
| In addition to the above patterns of solutions, there are other forms of integer solutions to (1). For illustration, whenα 0, the equation (6) is written as |
 (7) (7) |
| Write 1 as, |
 (8) (8) |
| or |
 (9) (9) |
| Using (4) and (8) in (7) and employing the method of factorization, define, |
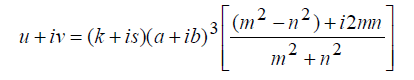 |
| Equating the real and imaginary parts, the values of u and v are obtained.Substuting these values of u and v in (2) and choosing a and b suitably, many different integer solutions to (1) are obtained. Similar process is carried out by considering (4) and (9). |
| To conclude one may search for other choices of solutions to (1) along with the corresponding properties. |
References |
|