ISSN ONLINE(2278-8875) PRINT (2320-3765)
ISSN ONLINE(2278-8875) PRINT (2320-3765)
Anjali.R1, Manju Rani Mathew1
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering
Biometrics plays a significant role in day to day life. It is widely used as a means of personal identification and authentication. Of this signature is most important. Handwritten signature is unique to an individual and virtually impossible to duplicate. This emphasizes the need for an automatic verification system. The aim of this paper is to measure gray level features of an image when it is distorted by a complex background and train by using neural network classifier and SVM. The practical signature verification problems include problems due to the need of segmenting the signature from the image document. This problem is overcome in this paper by calculating the gray level distortion and segmenting the original signature from the complex backgrounds. Then the image is trained by a neural network by using feed forward back propagation algorithm and SVM
Keywords |
||||||||||||||
| Back propagation algorithm, Gray-level distortion, neural network, Otsu’s threshold, support vector machine. | ||||||||||||||
I. INTRODUCTION |
||||||||||||||
| Biometrics plays a significant role in day to day life since it is widely used as a means of personal identification and authentication. Of these various biometric traits signature is the most important. Unlike a password or a PIN (identification data that can be forgotten, lost, stolen or shared), the captured values of the handwritten signature are unique to an individual and virtually impossible to duplicate. Signatures are accepted by governments and financial institutions as a legal means of verifying identity. This emphasizes the need for an automatic verification system. It decides whether or not a current test signature corresponds to a given reference signature. | ||||||||||||||
| The segmentation of the signature from the image document is the major problem in signature verifications in our practical life and in many cases it is impractical to segment the signature from a complex background. Presence of Gaussian noise caused by scanning of document, the different positions of the signature inside the document, presence of texture and logos in the background of the document, presence of stamps and typed text mixed with signature etc are some examples related to the extraction of signature from the document. | ||||||||||||||
| In this paper a method for removing or reducing the background complexity has been explained and extracting the original signature from the complex background. This extracted signature has also been analysed using a neural network classifier. Among the techniques that analyze the stroke thickness or stroke intensity variations, here we focus on the gray level distribution in the signature stroke. | ||||||||||||||
II. METHODOLOGY |
||||||||||||||
| The design of the system is divided into two stages. They are | ||||||||||||||
| i) Training Stage | ||||||||||||||
| ii) Testing Stage | ||||||||||||||
| The training stage consists of three major steps 1) Retrieval of a signature image from a database 2) Image preprocessing which includes image enhancement and background removal 3) Neural network training using back propagation feed forward algorithm and SVM [1]. | ||||||||||||||
| A Testing stage consists of four major steps 1) Retrieval of a signature to be tested from a database 2) Image preprocessing 3) Application of extracted features to a trained neural network 4) checking output generated from a neural network using back propagation feed forward algorithm and SVM. The block diagram of the proposed system is given in the Fig.1 below. | ||||||||||||||
| A. Database | ||||||||||||||
| The first step in the data-acquisition is the collection of signature samples to use for the evaluation of the respective study. The bigger the number of signature specimen the greater the probability of achieving accurate results. The database contains signed and unsigned cheques. Four individuals are asked to sign on cheques with varying background. They are asked to sign five cheques each. Six individuals signed on white paper and they also signed five times. Total sixty signatures were stored as database. Forgery sign of each signer is also taken. Twenty forgeries sign was also taken. The cheques and papers are scanned using a Canon Laser scanner and the images were stored as the test signatures and the database. | ||||||||||||||
| B. Conversion to gray scale image | ||||||||||||||
| Once the image is scanned, next step is to pre-process the image to improve the quality of the image. Preprocessing includes various techniques such as noise reduction, separating the signature from the background, binarization through the identification of an optimal threshold, data area cropping etc. The colour images are converted to gray scale images. | ||||||||||||||
| C. Back ground Removal | ||||||||||||||
| The individuals are asked to sign on bank cheques. Cheques differ in background complexity. But they can also be asked to sign on white paper. If they are signing in white paper it can be blended with the unsigned cheques to obtain an image with complex background. There are different types of blending modes: darken, multiply, colour or linear burn, lighten, colour or linear dodge etc. Here multiply blend mode is used which multiples the cheque image by the signature one. [2] | ||||||||||||||
| If I(x,y) be an image from the database and C(x,y) be an image of the check signing area both of 256-level gray scales and N and M indicates the pixels as shown in Fig.2. When blending the check and the signature some of the pixels outside of the strokes will be changed. In order to ensure that the pixels outside of the strokes remain unchanged [3], it is converted to black and white with a fixed threshold equal to 222 (strokes in white and the background in black) as shown in Eq(1) and is shown in Fig.3(a). | ||||||||||||||
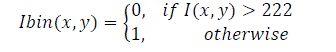 (1) (1) |
||||||||||||||
| Now the blended image ID(x,y) shown in Fig.3(b) is obtained by multiplying the pixels corresponding to the signature strokes as shown in Eq(2). | ||||||||||||||
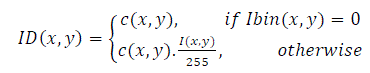 (2) (2) |
||||||||||||||
| The Gray level distortion Gd of each signature was calculated and is given as eqn (3) | ||||||||||||||
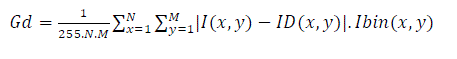 (3) (3) |
||||||||||||||
| Next there are two cases. | ||||||||||||||
| Case 1 | ||||||||||||||
| Back ground removal when there is no gray level distortion. | ||||||||||||||
| The background of the scanned signatures is well contrasted with the darker signature strokes. Therefore the signature images were first binarized by posterization. If I(x,y) be a 256-level, gray scale signature image of the database.[4] Then nl gray level posterized image shown in Fig.3(c) is defined as | ||||||||||||||
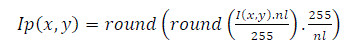 (4) (4) |
||||||||||||||
| where rounds (.) rounds the elements to the nearest integer. Here nl is taken as 3. By applying a single thresholding operation, we obtain the binarized signature Ibw(x,y) as | ||||||||||||||
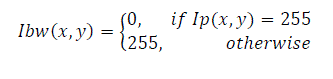 (5) (5) |
||||||||||||||
| This binarized image Ibw(x,y) shown in Fig.3(d) shows hair like artifacts which arises from the signature strokes. These artifacts can be eliminated by using an or- exclusive operation. This operation converts the white pixels to black if the left and right pixels are black or if the upper and lower pixels are black as shown in Fig.4 (a) and (b). | ||||||||||||||
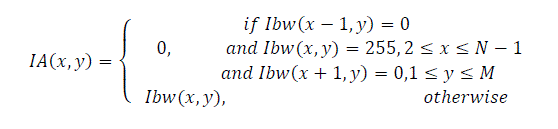 (6) (6) |
||||||||||||||
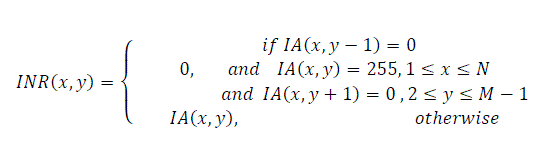 (7) (7) |
||||||||||||||
| The black and white INR(x,y) image is used to segment the original signature. The segmented signature IG(x,y) is obtained as in Eq(8) and is shown in Fig.4(d). | ||||||||||||||
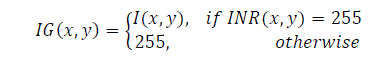 (8) (8) |
||||||||||||||
| Case 2 | ||||||||||||||
| Background removal when there is gray level distortion. | ||||||||||||||
| If the signatures are blended with the cheque images, this posterization procedure is not useful. This is because the background does not contain uniform character, lines and gray level textures. Here we use different background removal algorithms. | ||||||||||||||
| Two methods for signature segmentation are considered. First one is the segmentation of the database using the information from the original signature and the second is the use of automatic procedures to eliminate the background. | ||||||||||||||
| First method is that if I(x,y) be a 256-level, gray scale signature image of the database without gray level distortion and INR(x,y) be the same signature converted to black and white. Let ID(x,y) is the blended image with gray level distortion. The signature of ID(x,y) can be segmented as | ||||||||||||||
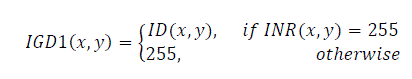 (9) (9) |
||||||||||||||
| where IGD1(x,y) the segmented signature shown in Fig.4(c) | ||||||||||||||
| Next method is the automatic signature segmentation on complex backgrounds. | ||||||||||||||
| In this method the signature is segmented from the signed cheque without using the original signature. Here the cheque is binarized by means of Otsu’s threshold. The resulting image contains the signature strokes plus several lines and text from the cheque with noise. Then the image is cleaned by removing the smaller objects. Along with this there are two additional processes. The first process eliminates the lines while the second one reduces the amount of residual text. The lines are eliminated by Hough transform. The beginning and end of each line is detected using Hough transform. Next the line width is detected; its pixels are turned to white except when the line crosses another object. | ||||||||||||||
| Text reduction is performed by obtaining the centroids of all the objects and selecting those that are lined up, elimination occurs when at least four objects are aligned to a similar height. A minimum height is required so that low pressure signature strokes which are similar to dotted lines are not erased. The final cleaned image shown in Fig.4(e) is given as the input to the neural network. The resulting signature is called INRD(x,y) and the signature automatically segmented with the gray level distorted is called IGD2(x,y) obtained in a similar way as in Eq.(9). | ||||||||||||||
| D. Training with a Classifier | ||||||||||||||
| After the background removal next step is to train and test the signature images. . Many classifiers can be used to train the network which includes support vector machine (SVM), neural networks, fuzzy sets etc. Here the paper focuses on the neural networks and SVM which are popular for their learning capability. An SVM [7] is a popular supervised machine learning technique which performs an implicit mapping into a higher dimensional feature space. This is called as kernel trick. Radial basis function (RBF) kernels are commonly used. In SVM feature extraction is done and the parameters are given in the form of matrices. Features such as local binary pattern (LBP) [6], local directional pattern (LDP), local derivative pattern (LDerivP) are taken and these parameters are used to train the network. The main disadvantage of using SVM is that it cannot be used for large database such as banking applications etc. Another demerit is that images cannot be directly given to train the network. These demerits can be overcome using neural network. | ||||||||||||||
| Backpropagation algorithm is a common method of training artificial neural networks. Classification is done using gradient descent with momentum and adaptive learning rate backpropagation. Gradient descent is used to reduce the error. After background removal the signatures are applied as input to train the neural network.[5] | ||||||||||||||
| The training parameters are given as | ||||||||||||||
| net.performFcn = mse; | ||||||||||||||
| net.trainParam.show =20; | ||||||||||||||
| net.trainParam.epochs =4800; | ||||||||||||||
| net.trainParam.mc = 0.95; | ||||||||||||||
| E. Verification | ||||||||||||||
| In the verification stage, the signature to be tested is extracted from the image by using the background removal equations as explained in section II-C. After that it is fed to the trained neural network which will classify the signature as genuine or forged. There are statistical error rates that affect the overall performance of the system. False Acceptance Rate (FAR), False Rejection Rate (FRR), and Correct Classification Rate (CCR) are the three parameters used for measuring the performance of the system. FAR and FRR are the error rates associated with verification and identification processes. In the analysis process it was found that number of forgeries accepted is 16 in SVM but it is only 9 in neural network. Number of originals rejected is 8 in SVM but it reduced to 4 in neural network. Number of samples correctly recognised is 60 in SVM whereas in neural network it is 71. Therefore CCR rate increased to 84.5% in neural network. | ||||||||||||||
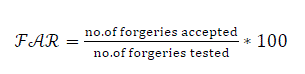 (10) (10) |
||||||||||||||
 (11) (11) |
||||||||||||||
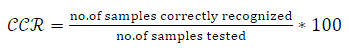 (12) (12) |
||||||||||||||
III. RESULTS AND DISCUSSION |
||||||||||||||
| For testing and training of the system many signatures were used which contains both the genuine and forged signature. These signature samples were applied in the testing phase to check whether the SVM and neural network classifies it correctly as genuine or forged. Random and simple forgeries are detected here. Here there are 60 signatures which belong to 12 peoples. Each people signed five times. So after training the samples in SVM, when these signatures were given for testing, it correctly identified the group to which the signature belongs as shown in the Fig.5. When forged signature and a signature which was not in the database were given, SVM cannot correctly identify the false signatures. Rather it showed the group to which the signature belongs closely as shown in Fig.6 and Fig 7. When training the samples in neural network, it correctly identified the group to which the signature belongs as shown in the Fig.5. But when a forged signature of the same was given it showed ‘wrong signature’ which is given in the Fig.6. This represents the simple forgery. Now if a signature which does not belong to the group was given, it also showed ‘wrong signature’. This represents a random forgery and is shown in Fig.7. | ||||||||||||||
IV. CONCLUSION |
||||||||||||||
| This paper presents a method for verifying handwritten signatures by using neural network architecture and SVM. In this paper a method for removing or reducing the background complexity using the gray level features has been introduced and the original signature has been extracted from the complex background. This extracted signature has also been analysed using SVM and neural network classifier. The neural network identified the group to which the signature belongs and simple and random forgery has also been identified whereas SVM only identified the genuine signatures in the database. Neural network was found to be better since it has good CCR. The proposed offline signature verification system has been tested with relatively small set of database. Future works entails using neural networks to identify the skilled forgery to increase the performance of the system. | ||||||||||||||
Figures at a glance |
||||||||||||||
|
||||||||||||||
References |
||||||||||||||
|