ON THE TERNARY QUADRATIC EQUATION

M.A.Gopalan; V.Sangeetha; Manju Somanath

ON THE TERNARY QUADRATIC EQUATION

M.A.Gopalan1,V.Sangeetha2,Manju Somanath3
Professor, Department of Mathematics,Srimathi Indira Gandhi College, Trichy, India1
Assistant Professor, Department of Mathematics, National College, Trichy, India2
Assistant Professor, Department of Mathematics, National College, Trichy, India3

Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology

Abstract

The ternary quadratic Diophantine equation 5 x2 + y2 − 9xy = 19z2 is analyzed for its patterns of non zero distinct integral solutions

Keywords

Integral solutions,Ternary quadratic

MSC 2000 subject classification number 11D09

INTRODUCTION

The Ternary Quadratic Diophantine Equation offers an unlimited field for research because of their variety [1, 2]. For an extensive review of various problems, one may refer [3-23]. This communication concerns with yet another interesting Ternary Quadratic Equation

for determining its infinitely many non-zero integral solutions.

II.METHOD OF ANALYSIS

The ternary quadratic equation to be solved in integers is

It is noted that (1) can be satisfied by the following triples of integers (1141a,379a,419a),(-2294A,1895A,2095A),(151a,a,77a),(746A,5A,385A),(305T,94T,115T), (-679A,470A,575A),(346a,91a,137a),(-911A,455A,685A),(1469A,355A,595A), (-166a,71a,119a),(481a,70a,215a),(-71T,14T,43T).

Now,introducing the linear transformations

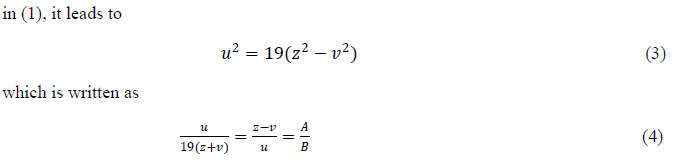which is equivalent to the system of equations

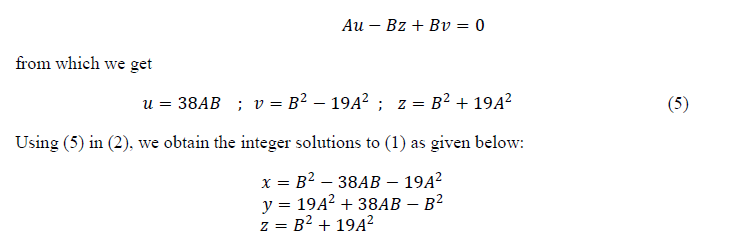It is observed that, by rewriting (4) suitably, one may arrive at the following three patterns of solutions to (1).

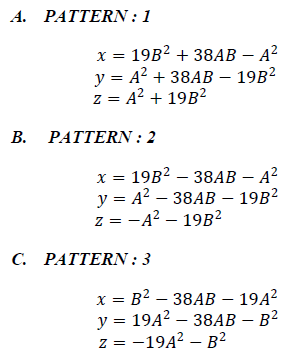However , we have another solution pattern which is illustrated below:

III.CONCLUSION

To conclude, one may search for other patterns of solutions to the equation under consideration.

References

L.E.Dickson, “ History of Theory of Numbers”, Vol.2, Chelsea Publishing Company,New York, 1952.
L.J.Mordell, “ Diophantine Equations”, Academic Press, London, 1969.
M.A.Gopalan, “Note on the Diophantine equation x2 + axy + by2 = z2” , Acta Ciencia Indica, vol.XXVIM(2), pp.105-106, 2000.
M.A.Gopalan, “Note on the Diophantine equation x2 + xy + y2 = 3z2” , Acta Ciencia Indica, vol.XXVIM(3), pp.265-266, 2000.
M.A.Gopalan,R.Ganapathy and R.Srikanth, “On the Diophantine Equation z2 = Ax2 + By2”, Pure and Applied Mathematika Sciences,vol.LII(1-2), pp.15-17,2000.
M.A.Gopalan and R.Anbuselvi, “On ternary Quadratic Homogeneous Diophantine Equation x2 + pxy + by2 = z2”,Bulletin of Pure and Applied Sciences,vol.24E(2),pp.405-408,2005.
M.A.Gopalan,S.Vidhyalakshmi and A.Krishnamoorthy, “Integral solutions of Ternary Quadratic ax2 + by2 = c(a + b)z2” Bulletin of Pure and Applied Sciences,vol.24E(2),pp.443-446,2005.
M.A.Gopalan,S.Vidhyalakshmi and S.Devibala, “Integral solutions of ka x2 + y2 + bxy = 4kα2z2”, Bulletin of Pure and Applied Sciences,vol.25E(2), pp.401-406,2006.
M.A.Gopalan,S.Vidhyalakshmi and S.Devibala ,“Integral solutions of 7x2 + 8y2 = 9z2”, Pure and AppliedMathematika Sciences,vol.LXVI(1-2),pp.83-86,2007.
M.A.Gopalan and S.Vidhyalakshmi, “An observation on kax2 + by2 = cz2”, Acta Cienica Indica, vol.XXXIIIM(1),pp.97-99, 2007.
M.A.Gopalan,Manju somanath and N.Vanitha, “Integral solutions of kxy + m x + y = z2”, Acta Cienica Indica, vol.XXXIIIM(4),pp.1287-1290, 2007.
M.A.Gopalan and J.Kaliga Rani, “Observation on the Diophantine Equation y2 = Dx2 + z2”,Impact J.Sci.Tech.vol.2(2),pp. 91-95, 2008.
M.A.Gopalan and V.Pondichelvi, “On Ternary Quadratic Equation x2 + y2 = z2 + 1”, Impact J.Sci.Tech.vol.2(2), pp.55-58, 2008.
M.A.Gopalan and A.Gnanam, “Pythagorean triangles and Special Polygonal numbers”, International Journal of Mathematical Sciences,vol.9(1-2),pp. 211-215, Jan-June 2010.
M.A.Gopalan and A.Vijayasankar, “Observations on a Pythagorean Problems”,Acta Cienica Indica,vol.XXXVIM (4), pp.517- 520, 2010.
M.A.Gopalan and V.Pondichelvi, “Integral solutions of Ternary Quadratic Equation Z X − Y = 4XY”, Impact J.Sci.Tech.vol.5(1),pp.1-6, 2011.
M.A.Gopalan and J.Kaliga Rani, “On Ternary Quadratic Equation X2 + Y2 = Z2 + 8”, Impact J.Sci.Tech.vol.5(1),pp.39-43,2011.
M.A.Gopalan,S.Vidhyalakshmi and T.R.Usharani, “Integral Points on the Homogeneous Cone 2z2 + 4xy +8x − 4z + 2 = 0”,Global Journal of Mathematics and Mathematical Sciences, vol.2 (1),pp.61-67,2012.
M.A.Gopalan,S.Vidhyalakshmi,T.R.Usharani and S.Mallika “Integral Points on the Homogeneous Cone 6z2 + 3y2 − 2x2 = 0”, Impact J.Sci.Tech.,vol.6(1),pp.7-13, 2012.
M.A.Gopalan,S.Vidhyalakshmi and G.Sumathi, “Lattice Points on The Hyperboloid of One Sheet 4z2 = 2x2 + 3y2 − 4”,Diophantus J.Math.vol.1(2),pp. 109-115,2012.
M.A.Gopalan,S.Vidhyalakshmi and G.Sumathi, “Lattice Points on The Elliptic Paraboloid 9x2 + 4y2 = z”,Advances in Theoretical and Applied Mathematics,vol.7(4),pp.379-385,2012.
M.A.Gopalan,S.Vidhyalakshmi and K.Lakshmi, “Integral Points on The Hyperboloid of Two Sheets 3y2 = 7x2 − z2 + 21”, Diophantus J.Math.vol.1(2),pp.99-107,2012.
M.A.Gopalan,V.Sangeetha and Manju Somanath, “Integral Points on the homogeneous cone z2 = 5x2 + 11y2”,Discovery Science,vol.3(7),pp.5-8, 2013.