ISSN ONLINE(2278-8875) PRINT (2320-3765)
ISSN ONLINE(2278-8875) PRINT (2320-3765)
S.Vadivazhagi1, Dr.N.Jaya2
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering
J.G. Ziegler and N.B. Nichols, after carrying out extensive experiments with different types of processes proposed certain tuning rules, that were readily accepted and till now are used as basic guidelines for tuning of PID controllers. This paper presents the online tuning of Two Tank Conical Interacting Level Process(TTCILP). This online tuning is based on simple experimental tests and is often required because the process models used to calculate the preliminary controller settings are not exact. There are different methods for online controller tuning. In this paper, the tuning method used for the process under study is Ziegler-Nichols (Z-N) tuning algorithm. The objective of this paper is to show that by employing the Z-N tuning, an optimization can be achieved. The performance of the PI controller based on Z-N tuning is verified by taking servo and regulatory responses in MATLAB/SIMULINK software environment. The controller provides satisfactory performance in both the cases.
Keywords |
||||||||||
| Two Tank Conical Interacting Level Process, PI controller, Z-N method, MATLAB/SIMULINK, ISE. | ||||||||||
I.INTRODUCTION |
||||||||||
| The control systems used for modern industrial plants typically include thousands of individual control loops as discussed by Dale Seborg et al (2004). Most of the industrial plants present many challenging problems due to their non linear dynamic behavior. Because of inherent non linearity, most of the chemical process industries are in need of traditional control techniques. One such non linear process taken up for study is Two Tank Conical Interacting Level Process. To achieve a satisfactory performance using conical tanks, its controller design becomes a challenging task because of its nonlinearity. Conventional controllers are widely used in industries since they are simple, robust and familiar to the field operator. It is well known that the Ziegler-Nichols continuous cycling tuning is the most popular method to tune the parameter settings of conventional PI controller. |
||||||||||
| The PI and PID controllers are widely used in many industrial control systems for several decades. Over 60 years ago, Ziegler and Nichols (1942) published a classic paper that introduced the continuous cycling method for controller tuning. D.Marshiana et al (2012) presented a paper on the design of Ziegler Nichols tuning controller for the non linear system such as conical tank. A simulink based model for analyzing the Z-N tuning algorithm for speed control of DC motor is presented by Bhaskar Lodh (2014). Chan Wooei Shyan et al (2013) discussed about different controller tuning rules for a hopper tank which has a non linear behavior. A comparison of PID controller tuning techniques is done by Anusha et al (2014) for the non linear conical tank process. |
||||||||||
| The paper is organized with following main headings. The mathematical modelling of conical interacting level process is described along with its operating parameters. Next, implementation of Z-N controller tuning is presented followed by the simulation studies which covers the servo and regulatory responses. Finally the paper ends with a conclusion which confirms that the controller designed offers satisfactory performance for a given set point. |
||||||||||
II. MATHEMATICAL MODELLING |
||||||||||
| The two tank conical interacting system consists of two identical conical tanks (Tank 1 and Tank 2), two identical pumps that deliver the liquid flows Fin1 and Fin2 to Tank 1 and Tank 2 through the two control valves CV1 and CV2 respectively as shown in Fig. 1. These two tanks are interconnected at the bottom through a manually controlled valve, MV12 with a valve coefficient β12. Fout1 and Fout 2 are the two output flows from Tank 1 and Tank 2 through manual control values MV1 andMV2 with valve coefficients β1 and β2 respectively. |
||||||||||
| The operating parameters of the interacting conical tank process is shown in Table.I | ||||||||||
| In this work, TTCILP is considered as two inputs two output processes in which level h1 in Tank 1 and level h2 in Tank 2 are considered as output variables and Fin1 and Fin2 are considered as manipulated variables. The mathematical model of two tank conical interacting system is given below as discussed by Ravi and Thyagarajan (2011). |
||||||||||
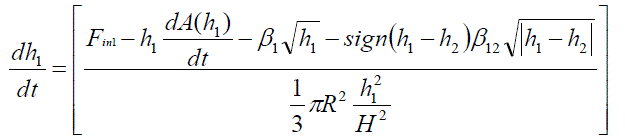 (1) (1) |
||||||||||
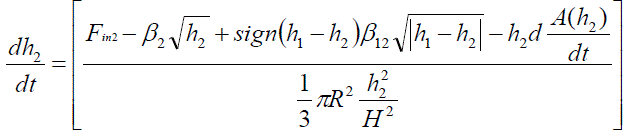 (2) (2) |
||||||||||
| where | ||||||||||
| A(h1) = Area of Tank 1 at h1(cm2) | ||||||||||
| A(h2) = Area of Tank 2 at h2(cm2) | ||||||||||
| h1= Liquid level in Tank 1 (cm) | ||||||||||
| h2= Liquid level in Tank 2 (cm) | ||||||||||
| Ziegler and Nichols presented a simple method for adjusting the controller when it is installed on an application, making use of the ultimate gain and period. For tuning the controller when the process is under closed loop operation, continuous cycling method can be opted. The ultimate gain (Ku) and ultimate period (Tu) of oscillation must be determined from the actual process by the following procedure as given by Carlos Smith and Armando Corripio in the Principles and Practice of Automatic Process Control (1997). |
||||||||||
| 1. Switch off the integral and derivative modes of the feedback controller so as to have a proportional controller. | ||||||||||
| 2. With the controller in closed loop, increase the proportional gain until the loop oscillates with constant amplitude. Record the value of gain that produces sustained oscillation as Ku , the ultimate gain. |
||||||||||
| 3. From the time recording of the controlled variable, the period of oscillation is measured and recorded as Tu. | ||||||||||
| 3. From the time recording of the controlled variable, the period of oscillation is measured and recorded as Tu. | ||||||||||
| P control: Kp = 0.5 Ku | ||||||||||
| PI control: Kp = 0.45 Ku, Ti = Tu / 1.2 | ||||||||||
| PID control: Kp = 0.6 Ku, Ti = Tu / 2, Td = Tu/8 | ||||||||||
| The controller settings obtained are tabulated below as shown in Table II. | ||||||||||
IV. SIMULATION STUDIES |
||||||||||
| An on-line tuning controller is designed for conical interacting level process and the performance is evaluated through MATLAB/SIMULINK software. The simulation is carried out by considering the nominal values of h1 and h2. (h1 = 28cm and h2 = 26cm). Servo and Regulatory responses are taken for tank1 and tank2. |
||||||||||
| Servo Performance | ||||||||||
| In servo operation the designed controller tracks the set point in a satisfactory manner. Figure 2 and 3 shows how the controller takes the operation for the given set point with respect to h1 and h2. |
||||||||||
| From the responses, it is inferred that the online tuning controller is able to maintain the tank levels h1 and h2 at the respective set points. The integral square error (ISE) obtained is tabulated in Table III. |
||||||||||
| Regulatory performance | ||||||||||
| In the regulatory operation, the disturbances are corrected automatically and the controller brings back the output to the desired level. Disturbances are introduced at output levels of h1 = 30cm and h2 = 30 cm. Figure 4 and 5 shows the regulatory response of conical interacting level process using Z-N tuned PI controller. |
||||||||||
| Simulation results show how the controller rejects the disturbance and brings back the plant back to the desired level. | ||||||||||
V. CONCLUSION |
||||||||||
| The strength of the ZN method is that it does not require a mathematical model, but controller parameters can simply be chosen by experimentation. Ziegler-Nichols method provides initial settings that will give satisfactory result, but it is always advisable to fine-tune the controller further for the particular process and better performance is expected to be achieved. |
||||||||||
Tables at a glance |
||||||||||
|
||||||||||
Figures at a glance |
||||||||||
|
||||||||||
References |
||||||||||
|