Research and Reviews - International Journals

International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Menu

ISSN ONLINE(2278-8875) PRINT (2320-3765)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

Optimal Control of Singular System via Walsh Function

Shilpa Arora
Assistant professor, Dept. of EE, Poornima College of Engineering, jaipur, Rajasthan, India
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Abstract

In first part the optimal control of singular system with a quadratic cost functional using walsh function is considered. After introducing walsh function in the beginning we develop an operational matrix for solving singular state equations. To demonstrate the validity and applicability of the technique, a numerical example is included



Keywords
Optimal control, singular system, orthogonal function, operational matrix, walsh function.

INTRODUCTION
Operational matrices were constructed using orthogonal functions for solving identification and optimisation problems of dynamic systems, was initially established in 1975 when the Walsh-type operational matrix was constructed by the present authors(Chen et al.,1965).Since then, many operational matrices based on various orthogonal functions, like Laguerre (Hwang et al.,1981 & King et al.,1979),Legendre(Chang et al.,1984),Fourier(Paraskevopoulos et al.,1985), and, Chebyshev (Paraskevopoulos et al.,1985), block pulse(Chen et al.,1977) had developed. Orthogonal functions deals with various problems of dynamic systems as it reduces the problems to those of solving algebraic equations. The operational matrix of integration eliminate the integral operation as in this approach differential equations are converted into integral equations through integration(Leila Ashayeri et al.,2012).
Singular system model is necessary for description of such a system which leads to the violation of casuality assumption. Singular systems also arise naturally in describing large scale systems; examples occur in power and interconnected systems(Iman ZamanI et al., 2011).
Optimal control of singular system via orthogonal functions has been presented, among others, by Balachandran and Murugesan(K. Balachandran et al.,1992), Shafiee and Razzaghi(M. Shafiee et al.,1998) and Razzaghi and Marzban (M. Razzaghi et al., 2002).
Very few work exist in the field of singular system therefore many challenging and unsolved problems have to face.

PRELIMINARY DEFINITION

A. Walsh function and its properties
A periodic function may be expanded into Fourier series. Analogously speaking, afunction, f(t), which is absolutely integrable in (0,1] may be expanded into series of Walsh.
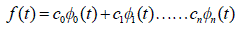image
where
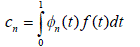image
are determined such that the following error is minimized:
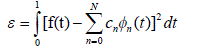image
image
where means taking the integer part of • and 1 1 , , , k k b b b is the binary number expression of i and ( ) k r t is the Rademacher function.
To draw the wave form of any Walsh function becomes a trivial matter if we use the above mentioned decomposition technique.
Let us then return to the Walsh coefficient evaluation for a function. Consider a given function f ( t ) = t. It is desired to expand it into Walsh series. Substituting the function f(t)= t into (2), we have
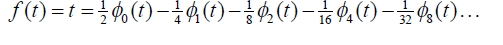image

B. Integration and operational matrix
In this section we will derive a method by which we can perform any integration by multiplying a constant matrix. Let us take Φ0 ,Φ1 Φ4.... and integrate them; we will have various triangular waves (Z.H.Jiang et al).If we evaluate the Walsh coefficients for these triangular waves, the following formula for approximation will be obtained:
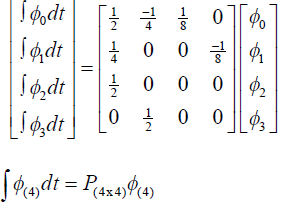image
The subscript means the dimension taken. It is preferable to take 2Ω , where Ω is an integer, as a dimension number. Making this choice will enable us to obtain simple results and easier calculation(Chih-Fan Chen et al.,1975). It is noted that
image

SINGULAR SYSTEM
Consider a singular system described by
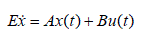image
image
Certain features of this case that are of special interest may be list, and will serve as points of contrast with the case of nonsingular case(G. C. Verghese et al.,1981).
1. The number of degrees of freedom of system is reduced to
f = rankE
2. The transfer function G(s) may no longer be strictly proper.
3. The free response of the system in this case exhibits exponential motions. In addition, however it may contain impulsive motions.
Definition: Singular system is regular if and only if there exists a scalarλ such that (λ E − A)−1 exists.

OPTIMAL CONTROL OF SINGULAR SYSTEM
In this section, we consider the LQR problem for linear time-invariant singular systems. Suppose that the optimization problem can be stated as follows: minimize
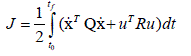image
and 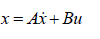image
For simplicity, we assume that Q and R are symmetric positive definite matrices. The Hamiltonian function is given by
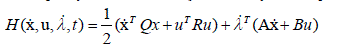image
Necessary conditions imply that
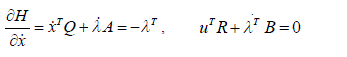image
that is,
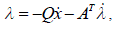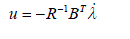image
image
where λ* satisfies the following equation:
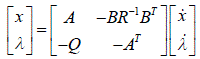image
and the boundary condition are specified as
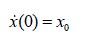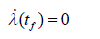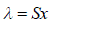image
image
image
where S is a constant matrix to be determined. Put this in (13) we get
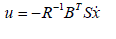image
Substituting (20) in (11),we get
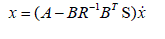image
By (14), (15), (19), (21), we have
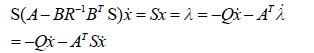image
that is
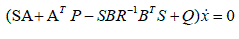image
Since this is true for any x* , we obtain the following Ricatti equation for singular system:
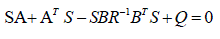image
By (20) , the optimal state derivative feedback control is given by (Yuan-Wei Tseng et al.,2013):
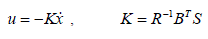image
And the closed loop system becomes
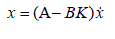image

WALSH SERIES SOLUTION TO THE PROBLEM
Firstly we normalize the problem because Walsh series is defined in the 0 to 1 interval
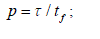image
Then (16) becomes
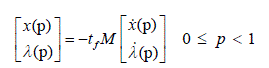image
Next, assume x*(p) and p* (p) to be expanded into Walsh series and we can determine its coefficients
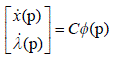image
where C is an 2nXm matrix, and Φ (p) ,an m-vector.
To perform integration on (29) eqn (6) is applied:
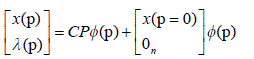image
Substituting (30) and (29) into (28) gives
Defining k as
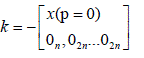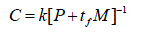image
image
Solving (32) forC ,we obtain the Walsh coefficients of the rate variable x*(p) rate co-state variable p* (p) .Then substitute them into (30) .The answer of x(p) and p(p) in terms of Walsh function are finally obtained.

RESULTS
Let us consider the example
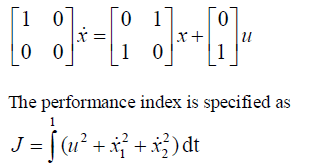image
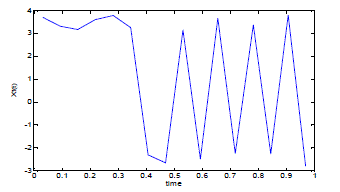
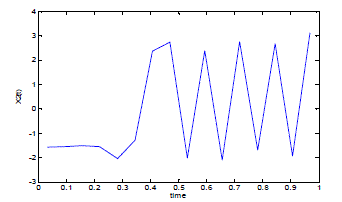
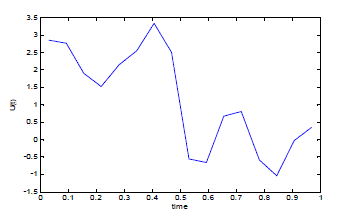
The the state variable x(t) and optimal control law u(t) are computed with m=4. Fig. 1, 2, 3. shows the result.
Fig.1 shows the trajectory of 1x (t) for m=4.The result can be improved by using higher values of m.
Fig.2 shows the state trajectory of x2 (t) for m=4.If resolution increases then time difference also increases.
Fig.3 shows the trajectory of optimal control u(t) for m=4 and tε [0,1).This is new approach for obtaining the optimal control of singular systems with quadratic cost function.

CONCLUSION
In this paper, a technique has been developed for obtaining the optimal control of singular systems with quadratic cost functional using walsh functions. The proposed approach is computationally simple. Since walsh functions are piecewise constant, one has to choose a large value for m in order to improve the accuracy.

Figures at a glance
Figure Figure Figure
Figure 1 Figure 2 Figure 3

References