Research and Reviews - International Journals

International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Menu

ISSN ONLINE(2278-8875) PRINT (2320-3765)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

Optimal Mother Wavelet for EEG Signal Processing

Arun Chavan1, Dr. Mahesh Kolte 2
  1. Assistant professor, Dept. of Biomed Engg., VIT, Wadala, Mumbai, India
  2. Prof. & Head , Dept. of EXTC, MIT, Pune, India
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Abstract

In the paper, wavelet analysis is applied to EEG. The wavelet transform is used to represent essential characteristics of EEG spikes and spike wave(SSW) complex with few coefficients. Since spikes contain high frequency energy, they will be represented in particular scale localized in a small time window. The wave portion of the spike wave complex will be represented in a lower scale of WT, covering wider span of time. Thus with the proper selection of WT scales and time spans a fewer number of WT coefficients may be used to represent the SSW complexes[6].In order to reduce the false detection, we can extend the contextual information by referring to other signals such as EOG for information about eye movements, EMG (Electro Myo Gram) for information about muscle electrical activity. With this it is possible to reduce greatly the false detection of sharp transients due to artifacts.[3]



Keywords
Wavelet Analysis, EEG, STFT, WT.

INTRODUCTION
Wavelets are an efficient tool for analysis of short-time changes in signal morphology. As pointed out by Unser and Aldroubi in [8], the preferred type of wavelet transform for signal analysis is the redundant one that is continuous wavelet transform in opposition to the non-redundant type corresponding to the expansion on orthogonal bases ( multi resolution analysis). The reason is that the CWT allows decomposition on an arbitrary scale. Thus, frequency bands of interest can be studied properly at chosen resolution. Wavelet theory provides a unified framework for a number of techniques developed for various signal-processing applications. Particularly, it is of immerse interest for the analysis of non-stationary signals like EEG, because it provides an alternative to the classical Short-Time Fourier Transform (STFT) or Gabor transform. The basic difference is, in contrast to the STFT, which uses a single analysis window, the Wavelet Transform (WT) uses short windows at high frequencies and long windows at lower frequencies. This is similar to “Constant Q” or Constant relative bandwidth frequency analysis.[6]For some applications WT can be seen as signal decomposition onto a set of basis functions. Basis functions called Wavelets are obtained by a single prototype wavelet by dilation and contraction (Scaling) as well as shifts. The prototype wavelet can be thought of as a band pass filter, and the constant Q property of the other band pass filter (Wavelets) follows because they are scaled version of prototype.[6]Therefore, in a WT, the notion of the scale is introduced as an alternative to frequency leading to time scale representation. It means that a signal is mapped into a time-scale plane as compared to the time frequency plane used in the STFT.[6]

LITERATURE SURVEY
Despite advances in the development of drugs for the control of seizures, there are still many individuals with pharmacoresistant epilepsy . Recent conferences suggested the use of animal models of chronic epilepsy to facilitate the development and testing of more efficacious drugs [13]. Because of the volume, human review of the data is impractical. An automated system is required to increase accuracy and speed of analysis. Artificial neural networks have been used for EEG analysis for disease diagnosis, sleep-stage classification, mental-state classification, artifact recognition, and the detection of epileptiform discharges. The radial basis function (RBF) neural networks are used to identify seizure or preseizure states. As input to the RBF networks we can use raw EEG data, coefficients from wavelet decomposition of the raw data. An RBF network consists of an input layer, a single hidden layer, and an output node [12]. In addition to demonstrating a reliable seizure identification method, the possibility of predicting an impending seizure before clinical onset can also be investigated. The period during a seizure is known as the ictal state, while the periods of normal brain activity between seizures are called inter-ictal. A third state, referred to as pre-ictal, has been defined as the period just before seizure onset. If this state can be identified in the EEG [9] seizures can effectively be predicted, resulting in an early warning to the patient. This would also facilitate the use of implantable devices that would abort a seizure, eliminating the need for prophy-lactic drug treatment [10]. The field of seizure identification has been around for many years and many techniques have been refined to accurately identify either focal or generalized seizures. These methods can directly employ use of the EEG data or may involve transformations. The attempt to identify a pre-ictal state began much more recently and has been shown to be a much greater challenge [9],[10],[11]. Early attempts at identifying seizures used the EEG data directly . These attempts met with some success, but more subtle seizures and those associated with a noisy signal were often missed.
More recently, more sophisticated algorithms have been used, yielding increasingly accurate results. For example, visual inspection of wavelet-transformed EEG from an epileptic patient was used, where the Daubechies wavelet decomposition was found superior to the short-time Fourier transform for its ability to localize and identify the transient signals associated with epileptic discharges. There is extensive literature concerning the use of neural networks in EEG interpretation. Seizure prediction is some what controversial because it has not been proven that there is a “pre-ictal state” during which the brain functions differently than in the inter-ictal state. It is further uncertain whether or not this proposed difference in functioning is evident on an EEG. Most methods of seizure prediction employ nonlinear techniques. A review of seizure pre-ictal state identification research was published in [9]. It is pointed out in [12] that estimates of fractal dimension of EEG data are almost certain to be incorrect; however, relative differences between estimates using the same method may be useful in distinguishing between states. In [11], a dimensionality decrease was noted in human EEG data hours before seizure onset, indicating an increase in the correlated neural activity. This finding has not been reproduced by other authors. The earliest study of pre-ictal state identification to use wavelet decomposed data with a neural network was reported in [14]. They used recurrent neural networks with one or two inputs, ten or 15 recurrent hidden neurons, and one output neuron. Daubechies wavelets were used to decompose the raw data, and only data from the most relevant intracranial probe were used. Separate networks were trained with raw data, wavelet approximation coefficients, and detail coefficients. The students from Amirkabir University of Technology, Tehran, have used wavelet packet transform to the EEG signal in order to decompose it into frequency sub-bands, before being introduced to the neural network. In the study they have applied a genetic algorithm (GA) learning method with different fitness functions to optimize the neural network. The network has been tested for EEG signals that are provided from BCI and the results show the power of ANN in processing of noisy nature signals as EEG signals [15].

[A] EEG Analysis Methods
 Nonparametric Methods
 Amplitude distribution
 Interval or period Distribution
 Amplitude – interval Scatter plots
 Correlation functions
 Auto – and Cross- Correlation
 Complex demodulation
 Power Spectrum analysis
 Time – varying spectra
 Cross- spectral functions ( coherence and phase )
 Bispectra
 Walsh and Haar transforms
 Parametric Methods
 Autoregressive and ARMA Models
 Time- varying signals : Kalman filtering
 Segmentation Analysis.
 Mimetic Analysis
 Template Matching
 Topographic Analysis

[B] Limitations of Conventional EEG Analysis
From the earliest days of electroencephalography it has been realized that the records are complex. Even when great care is taken to restrict the effective size and separation of electrodes so as to reduce the area from which activity is recorded, it is only rarely that a pure and simple oscillation is observed. This puts a heavy burden on the experimenter, for the human eye and brain are very poorly adapted to the analysis of a complex curve.
1) Masking – When a record contains two simple pure components of unequal size, only the larger one is readily appreciated when the frequencies differ by less than a factor of about four. The larger rhythm is said to “mask” the smaller, which cannot be readily measured in the record. When the frequency of the smaller rhythm is more than about four times that of the larger, the small fast rhythm can be seen more easily ,as a “ripple” superimposed on the larger slow waves.
2) Beats: - When the frequencies of two rhythm are closer together in ratio 2 to 3 , the record shows periodic fluctuations of amplitude at a frequency equal to difference between the frequencies of two rhythms , and the rhythms are said to be “bear” with one another.
3) Waveform distortion: -When the frequency ratio of their rhythm lies between 2 and 3 and 1 to 4 the rhythms distort one another. Only the frequency of larger one can be measured directly.
4) Modulation:- When there are three rhythms such that the frequencies of two of them are at equal intervals on either side of frequency of the third , which is largest of the three, the record shows periodic fluctuations of amplitude at a frequency equal to half the difference between the frequencies of the upper and lower components.

WAVELET TRANSFORM

[A] Wavelet Transform
The wavelet transform of a sigmoid x(t) is defined as
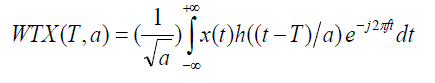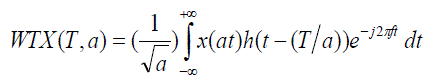image
image
In WT, analysis of a signal is carried out by the use of a special function, h(t) , called the mother wavelet. This function is translated in time for selecting that part of the signal to be analysed. The portion of the signal selected is then expanded or contracted using a scale parameter, a, which is analogous to frequency. For small values of a, the wavelet is a narrow function of the original function, which corresponds roughly to higher frequencies. For very large values of a , the wavelets are expanded and correspond to low frequency. In the WT, high frequency components are analysed with the sharper time resolution than low frequency components. This is desirable properly, especially in analysing fast transient waveforms such as EEG spikes. [6] The functions WTX ( T,a ) is the projection of signal onto the wavelet shifted by T and scaled by a , and hence indicates the contribution of wavelet to the signal. Thus, such a transformation does not lead to time- frequency representation but instead, to, time – scale decomposition in which scales are related to frequency.

[B] Advantages of wavelet transform
1] The Fourier transform represents a signal as combination of scaled and phase shifted sinusoids. Wavelet decomposition represents a signal as a combination of scaled wavelets; the mother wavelet shape selected depends on the application.
2] The Discrete Fourier transform assumes that the signal is periodic and in the case of non – periodic signals complex techniques must be used to estimate the Fourier components without misrepresentation. Wavelets decomposition is naturally amenable to represent non- periodic functions.
3] The wavelet expansion allows a more accurate local description and separation of signal characteristics. A Fourier coefficient represents a component that last for all time and therefore, temporary events must be described by a phase characteristics that allows cancellation or reinforcement over large time periods. A wavelet expansion coefficient represent a component that is itself local and is easier to represent.
4] The Fourier transform acts on a block of data simultaneously, therefore, information about the location of different components within the block is not available. In wavelet decomposition the time location of the wavelets is known directly from the position of the output Wavelet coefficients.
5] The Fourier transform has equal time and frequency resolution for all the components. Wavelet decomposition has a large time aperture, but closely spaced frequency resolution for slow components ; and small time aperture but broad frequency resolution for fast components.

RESULTS AND CONCLUSION
The purpose of the study was to investigate the feasibility of using wavelet transform as a preprocessor for EEG spikes detection system. The study aimed at decreasing the information content of the signal without degrading the detection performance. Since routine clinical EEG requires recording from many channels (generally 32 to 44 ) , input size becomes a critical design parameter for real – time multichannel spike detection systems. The results of the study now that the use of the WT drastically decrease the input size, without much compromise in performance. The most important factor in performance, however, was the proper selection of the scale. Scale 4 performed the best for the Haar as well as Daubechies Wavelets indicating that it contained most content of the relevant information for detection. [2]
In the following figures the sample waveforms for channel-2 are shown.
Out of two wavelets analyzed namely Haar (Daub-1), Daub-4, it was found that Daub-4 gives good results. Daubechies Wavelets were found suitable for analysis due to the compact support and their similarity with the SSW wave. Programs can be developed to display the sample waveform for different channels, for decomposition of the waveform using DB-1 & DB-4 as well as for the display of original, de-noised and compressed waveforms for each channel.
In order to reduce the false detection. we can extend the contextual information by referring to other signals such as EOG( Electro-oculogram) for information about eye movements, EMG( Electro myogram) for information about electrocardiography activity. With this it is possible to reduce greatly the false detection of sharp transients due to artifacts. For more reliable detection of epilepsy , number of clinical and pathological information such as age, sex , body temperature , pulse rate , body sugar etc. and behavioral status of patient like co-operative or non co-operative , Introvert or extrovert , right handed or left handed etc. and different EEG recording with photic stimulations, hyperventilation may be used. Although in this study, the accuracy of Daub-4 found to be satisfactory, other type of wavelets such as morlets wavelet or spline wavelets need to be analyzed. Designing the mother wavelet that matches the shape of frequency characteristics of Spike and Spike Wave (SSW) events may also offer higher accuracy. These possibilities are open for future studies. The method was implemented and tested off-line. However, this can be further extended for on-line implementation by taking into account memory management and computational load. This method can be further extended with ANN to classify the EEG into normal or abnormal depending upon its frequency distribution. It can be extended to further classify the abnormalities. In order to replicate the reasoning of EEGer, the expert system provided with the knowledge of spatial context may be designed. Finally, the system must be evaluated by comparing its performance after applying it to large number of abnormal cases, including normal cases with visual scoring by EEGer.

Figures at a glance
Figure Figure
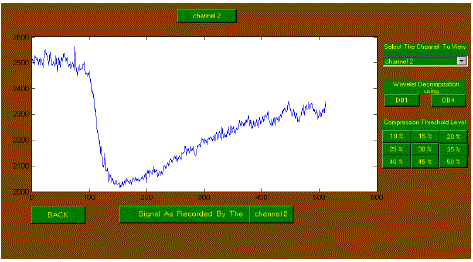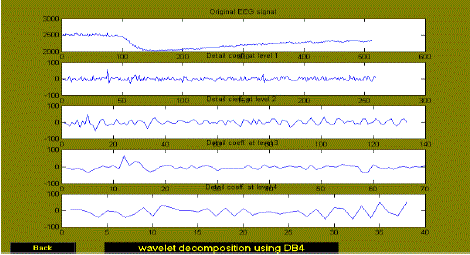Figure 1 Figure 2

References