Research and Reviews - International Journals

International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Menu

ISSN ONLINE(2278-8875) PRINT (2320-3765)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

Optimal Placement of PMU for Power System Observability

Parth Patel1, Jigar Tailor2, Chinmay Naik3
  1. PG Student [Power Systems], Dept. of EE, C. G. Patel Institute of Technology, Bardoli, Gujarat, India
  2. PG Student [Power Systems], Dept. of EE, C. G. Patel Institute of Technology, Bardoli, Gujarat, India
  3. Assistant Professor, Dept. of EE, C. G. Patel Institute of Technology, Bardoli, Gujarat, India
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Abstract

Phasor Measurement Unit (PMU) is a relatively new technology that, when employed in power networks, offers real-time synchronised measurements of the voltages at buses and currents along the lines that connect them. This is accomplished by using a GPS based monitoring system which facilitates time synchronisation of measurements and unlike SCADA, makes the measured data available in Real-Time format. SCADA is not able to provide Real-time data due to the low speeds at which RTUs (Remote Terminal Units) provide data. Availability of time-stamped phasor measurements makes PMUs preferable for power system monitoring and control applications such as State Estimation, Instability Prediction Analysis, Real time monitoring of the system conditions, Islanding Detection, System Restoration and Bad Data Detection. Since PMUs are expensive, their procurement and installation needs to be planned both in terms of economy and utility. Usually utilities like to see that the power network becomes fully observable with minimum number of PMUs placed at strategic buses. Where full observability refers to all the buses in the network are actively monitored. Thus the problem of optimal placement of PMUs is formulated as an optimization problem where the number of PMUs is minimized subject to complete system observability. This paper solves the optimal placement of PMUs for power system observability using Integer Linear Programming (ILP) methodology. The method is tested on IEEE 14 Bus System.

Keywords
Integer Linear Programming, Phasor Measurement Units, Power System Observability.

I.INTRODUCTION
Phasor Measurement Units are important devices in Wide Area Measurement, Protection and Control system studies. PMU is a monitoring device, which can provide synchronized measurement of voltage and current phasor in a power system. Synchronized signals are achieved from Global Positioning System (GPS) satellites [4].Synchronicity in PMU is achieved by time stamping of voltage and current waveforms using a common synchronizing signal available from the GPS [6].
PMU measurements, in compare with SCADA system are taken at higher speed. Time stamping of each measurement; provides the precise view of the entire network interconnections. In recent years, due to high cost of having PMU at each node of the network, several research activities have been performed to locate minimal set of PMUs in order to make the power system completely observable, with considering different operation conditions [4].
PMU placement at all substations allows direct measurement of the state of the network. However, PMU placement on each bus of a system is difficult to achieve either due to cost factor or due to nonexistence of communication facilities in some substations. Moreover, as a consequence of Ohm’s Law, when a PMU is placed at a bus, neighboring busses also become observable. This implies that a system can be made observable with a lesser number of PMUs than the number of busses.
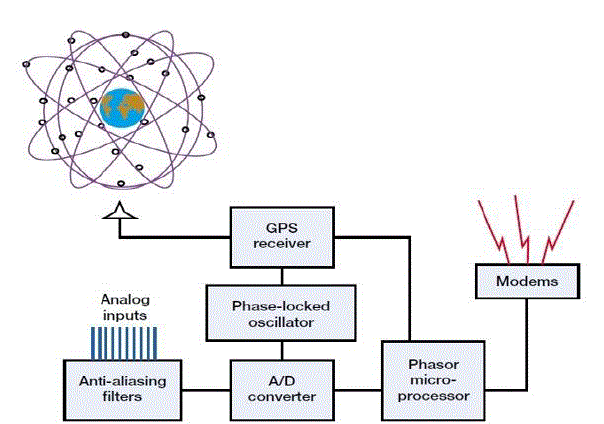
A PMU is a measurement processing device which is connected to buses at substations. The PMU makes use of measured currents and voltages from voltage and current transformers. This is received in an analogue form and is processed by an anti-aliasing filter which removes all components of the signal larger than half the Nyquist sampling rate [5].
The measurement signal is then put through an Analogue to Digital Converter (ADC). The digitised measurement is thereafter time-stamped by the GPS clock. The digital samples go through a microprocessor which converts the measurements into a phasor form of data. Now the measured sample is ready to be sent to the Phasor Data processor (PDC). The PDC can be compared to a mini-control centre, only there may be multiple PDCs in a system. In other words, singular centralised control is not necessary. Figure
For systems of 50 to 60 Hz, 50 to 60 samples are provided per second respectively by the PMU. Figure shows a diagram of control blocks of a PMU.The actual phasor is derived from the complex voltage and current sinusoidal waveforms of the measured buses. PMUs measure the voltage phasor of the resident bus and current phasors in the lines connecting the adjacent buses.
Phasor Measurement Units (PMU) allow the observer to get measurements of voltage phasor of all the bus as well as the phasor currents for all lines incident to that bus. PMU placement at all substations allows direct measurement of the state of the network. However, PMU placement on each bus of a system is difficult to achieve either due to cost factor or due to nonexistence of communication facilities in some substations. Moreover, as a consequence of Ohm’s Law, when a PMU is placed at a bus, neighboring busses also become observable. This implies that a system can be made observable with a lesser number of PMUs than the number of busses.
In Reference [2] a unified approach is developed to find the minimum number and locations of PMUs such that the power network is observable. In addition, it accounts for the existing conventional measurements in the mathematical model of the optimal PMU placement strategy. Reference [3] presents an algorithm that avoids iterative addition of measurements and allows simultaneous placement of PMUs for observability analysis. Presented method in reference [4] proposes a method to place PMUs in the power system optimally in the cases of loss of normal operating and in the case of any single PMU or single branch from the network. The method in reference [5] proposes a generalized integer linear programming formulation for optimal PMU placement under different cases. In reference [6] the proposed model is used to determine the optimal number and location of PMUs to make the system observable.

II.SOBJECTIVE AND ASSUMPTIONS
PMU placement for Power System Observability is the main focus of this paper. The algorithm must produce placement solutions that are cost effective and either similar to or better than placements of other algorithms. The following assumptions were made during the process of this paper:
1. All PMUs cost the same.
2. There are sufficient telecommunication facilities for PMU operations.
3. The proposed network does not utilize any existing conventional measurements and/or zero injections.

III.OBSERVABILITY ANALYSIS
Observability Analysis is a fundamental component of real time state estimation. Observability analysis of electric power system is to study whether there is enough measurement in system in order to estimate the state of electric power system including the amplitude value and phase angle of the voltage.If the voltage of a node can be measured directly or can be calculated by other voltage phasor or current phasor, the node is observable.

IV.PROBLEM FORMULATION
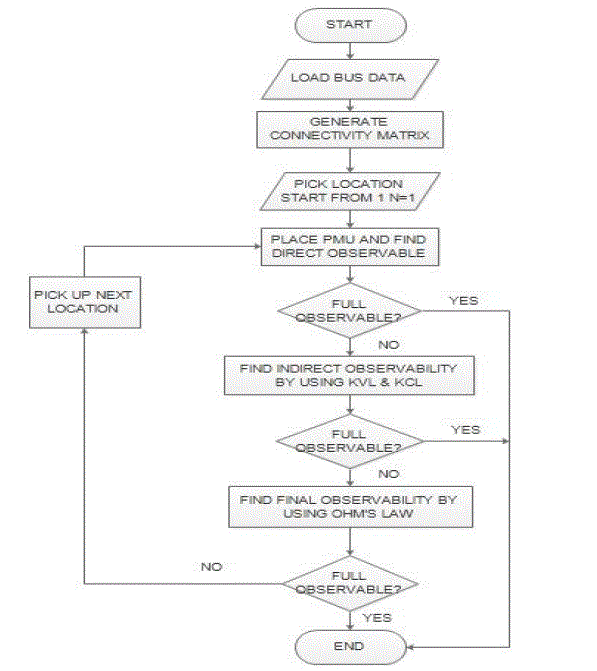
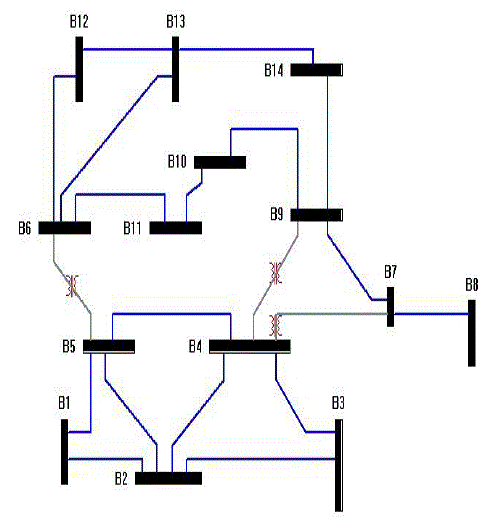
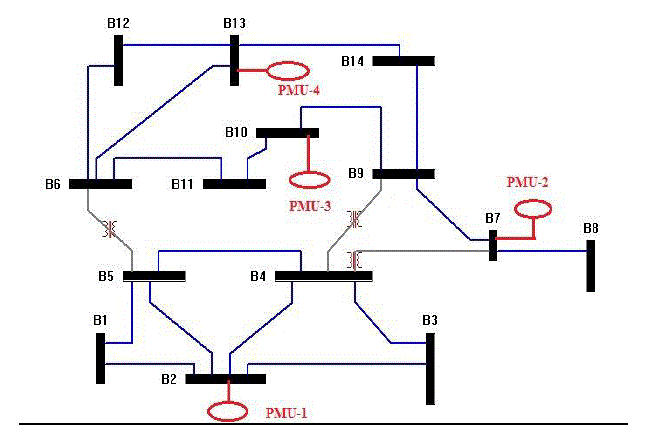
The minimum PMU placement problem is NP-complete, which can be solved by either mathematical algorithm or heuristic algorithm.The number of PMUs will have to be minimised due to cost and communication line availability. Consider the IEEE 14 Bus System and its measurement configuration shown in Figure 3. The task of optimal PMU placement can be solved by using a binary integer linear programming approach [5].
The objective function is given below:
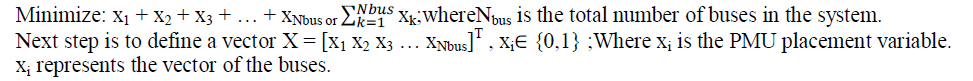image
The constraints are thus given as equation AX ≥ b_L
Where b_L is a vector: [1 1 1 . . . 1]T, which generates the constraint that each bus must be observed by at least one PMU. The algorithm for Integer Linear Programming is shown in Figure 2.

V. SIMULATION RESULT
The presented method in this paper is programmed on MATLAB and binary integer linear programming problem has been solved in order to find the best PMU placement with complete Power System observability and minimum installation cost.In order to examine the validity of the proposed algorithm, it has been tested on IEEE 14-bus as shown in Figure 3.
The technical specifications of the computer used for these simulations are given in Table I
Integer Linear programming problem is solved in MATLAB using the TOMLAB Optimization Toolbox [1]. Table 2 shows the results of optimal PMU placement for the IEEE 14-bus system, which has no other conventional power flow or injection measurements.
The graphical representation is shown in Figure 4. The four PMUs installed at bus 2, bus 7 and bus 10, and bus 13 can make the whole system observable.

VI.CONCLUSION
A generalized method based on binary integer linear programming is used to find the optimal number and location of PMUs, to make whole system completely observable. Keeping entire system observable in case of any contingencies and minimizing total installation cost are the main aims of this paper.

Tables at a glance
Table icon Table icon
Table 1 Table 2
 

Figures at a glance
Figure 1 Figure 2 Figure 3 Figure 4
Figure 1 Figure 2 Figure 3 Figure 4
 

References