Research and Reviews - International Journals

International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Menu

ISSN ONLINE(2278-8875) PRINT (2320-3765)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

Optimal Placement of Shunt Connected Facts Device in a Series Compensated Long Transmission Line

Hari konidala1, Y. N. Vijay kumar2
  1. M.Tech (PE&ED) Student, Department of EEE, SVCET, India
  2. Associate Professor, Department of EEE, SVCET, India
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Abstract

Static VAR Compensator (SVC) and Static Synchronous Compensator (STATCOM) are important devices in FACTS family, and is widely recognized as an effective and economical means to solve the power system stability problem. SVC and STATCOM are used as shunt in transmission system. In the present work a series compensated Distributed transmission line (345KV, 450km, 50Hz) with a shunt FACTS devices SVC and STATCOM is considered to the optimal location of the shunt FACTS devices to get the highest possible benefits of maximum power transfer and system stability. Effect of change in degree of series compensation on the optimal location of the shunt FACTS device to get the highest possible benefit is studied. It is found that the optimal location of the shunt FACTS device varies with the change in the level of series compensation to get the maximum benefit in terms of power transfer capability and stability of the system. All the simulations for the above work have been carried out using MATLAB /SIMULINK software.

Keywords
optimal placement, SVC, STATCOM, degree of series compensation, long transmission line etc.

LITERATURE SURVEY
During the last decade a number of control devices under the term Flexible AC Transmission Systems (FACTS) technology have been proposed and implemented. The FACTS devices can be used for power flow control, loop flow control, load sharing among parallel corridors, voltage regulation [1].The basic concepts of the proposed generalized power flow controller that is able to maintain prescribed, and independently controllable, real power and reactive power powerflow in the line [2]. The term and definition of various FACTS devices are described in references [3, 4].

I. INTRODUCTION
The FACTS controllers offer a great opportunity to regulate the transmission of alternating current (AC), increasing or diminishing the power flow in specific lines and responding almost instantaneously to the stability problems. The potential of this technology is based on the possibility of controlling the route of the power flow and the ability of connecting networks that are not adequately interconnected, giving the possibility of trading energy between distant agents. It is meant to enhance controllability and increase power transfer capability. It is generally power electronics based device. The FACTS devices can be divided in three groups, dependent on their switching technology: mechanically switched (such as phase shifting transformers), thyristor switched or fast switched, using IGBTs. While some types of FACTS, such as the phase shifting transformer (PST) and the static VAR compensator (SVC) are already well known and used in power systems, new developments in power electronics and control have extended the application range of FACTS.
Furthermore, intermittent renewable energy sources and increasing international power flows provide new applications for FACTS. The additional flexibility and controllability of FACTS allow to mitigate the problems associated with the unreliable of supply issues of renewable. SVCs and STATCOM devices are well suited to provide ancillary services (such as voltage control) to the grid and fault rid through capabilities which standard wind farms cannot provide Furthermore, FACTS reduce oscillations in the grid, which is especially interesting when dealing with the stochastic behaviour of renewable.
The SVC provides an excellent source of rapidly controllable reactive shunt compensation for dynamic voltage control through its utilization of high-speed thyristor switching/controlled reactive devices. An SVC is typically made up of the following major components:
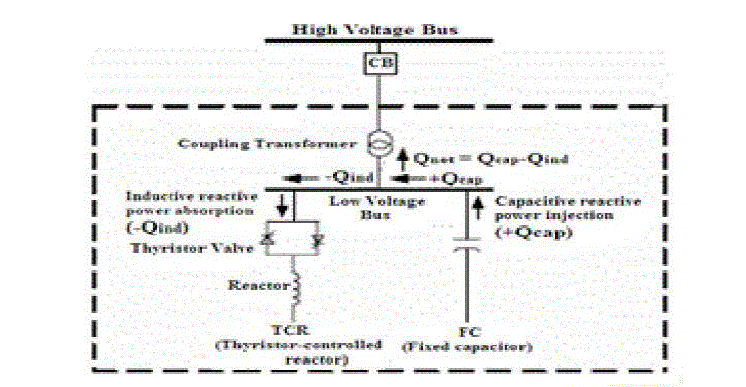
Coupling transformer
Thyristor valves
Reactors
Capacitors (often tuned for harmonic filtering)
In general, the two thyristor valve controlled/switched concepts used with SVCs are the thyristor-controlled reactor (TCR) and the thyristor-switched capacitor
A. Dynamic Response of the SVC
When the SVC is operating in voltage regulation mode, its response speed to a change of system voltage depends on the voltage regulator gains (proportional gain KP and integral gain Ki, the droop reactance X , and the system strength (short circuit level). For an integral-type voltage regulator (KP = 0), if the voltage measurement time constant Tm and the average time delay Td due to valve firing are neglected, the closed-loop system consisting of the SVC and the power system can be approximated by a first-order system having the following closed-loop time constant.
B. Description of Static VAR Compensator
The static VAR compensator (SVC) is a shunt device of the flexible AC transmission systems (FACTS) family using power electronics to control power flow and improve transient stability on power grids. The SVC regulates voltage at its terminals by controlling the amount of reactive power injected into or absorbed from the power system. Each capacitor bank is switched on and off by three thyristor switches (Thyristor Switched Capacitor or TSC). Reactors are either switched on-off (Thyristor Switched Reactor or TSR) or phase-controlled (Thyristor Controlled Reactor or TCR).
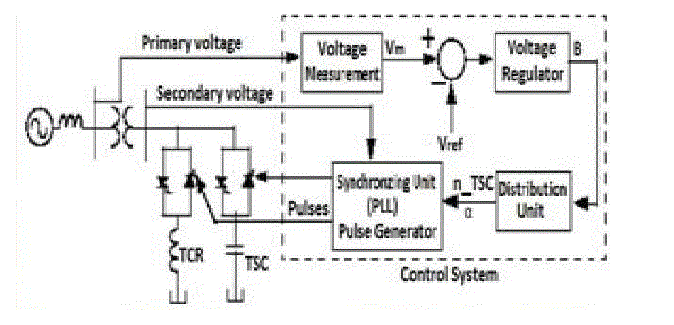
C. Single-line Diagram of an SVC and Its Control System
The control system consists of, -A measurement system measuring the positive-sequence voltage to be controlled. A Fourier-based measurement system using a one-cycle running average is used. A voltage regulator that uses the voltage error (difference between the measured voltage Vm and the reference voltage Vref) to determine the SVC susceptance B needed to keep the system voltage constant. A distribution unit that determines the TSCs (and eventually TSRs) that must be switched in and out, and computes the firing angle M of TCRs. A synchronizing system using a phase-locked loop (PLL) synchronized on the secondary voltages and a pulse generator that send appropriate pulses to the thyristor.
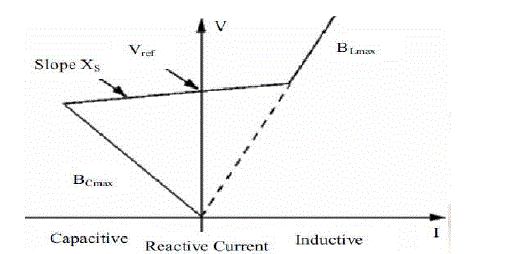
D. SVC V-I Characteristic
The SVC can be operated in two different modes: In voltage regulation mode and in VAR control mode (the SVC susceptance is kept constant) when the SVC is operated in voltage regulation mode, it implements the following V-I characteristic. As long as the SVC susceptance B stays within the maximum and minimum susceptance values imposed by the total reactive power of capacitor banks (BCmax) and reactor banks (Blmax) the voltage is regulated at the reference voltage Vref . However, a voltage droop is normally used (usually between 1% and 4% at maximum reactive power output), and the V-I characteristic has the slope indicated in the Figure.4.The V-I characteristic is described by the following three equations: SVC is in regulation range (−BCmax < < Blmax )

III. MODELING OF THE STATCOM
A. Configuration
STATCOM is one of the important shunt connected Flexible AC Transmission Systems (FACTS) controllers to control power flow and make better transient stability. The basic structure of STATCOM in schematic diagram is shown in Figure 6. It regulates voltage at its terminal by changing the amount of reactive power in or out from the power system. When system voltage is low, the STATCOM inject reactive power. When system voltage is high, it absorbs reactive power.
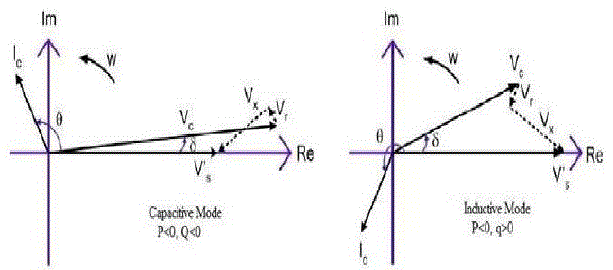
B. Phase angle control
In this case the quantity controlled is the phase angle δ. The modulation index “m” is kept constant and the fundamental voltage component of the STATCOM is controlled by changing the DC link voltage. By further charging of the DC link capacitor, the DC voltage will be increased, which in turn increases the reactive power delivered or the reactive power absorbed by the STATCOM. On the other hand, by discharging the DC link capacitor, the reactive power delivered is decreased in capacitive operation mode or the reactive power absorbed by the STATCOM in an inductive power mode increases. For both capacitive and inductive operations in steady-state, the STATCOM voltage lags behind AC line voltage (δ> 0).
By making phase angle δ negative, power can be extracted from DC link. If the STATCOM becomes lesser than the extracted power, Pc in becomes negative and STATCOM starts to deliver active power to the source. During this transient state operation, Vd gradually decreases. The phasor diagrams which illustrating power flow between the DC link in transient state and the ac supply is shown in above Figure 5. For a phase angle control system, the open loop response time is determined by the DC link capacitor and the input filter inductance. The inductance is applied to filter out converter harmonics and by using higher values of inductance; the STATCOM current harmonics is minimized.
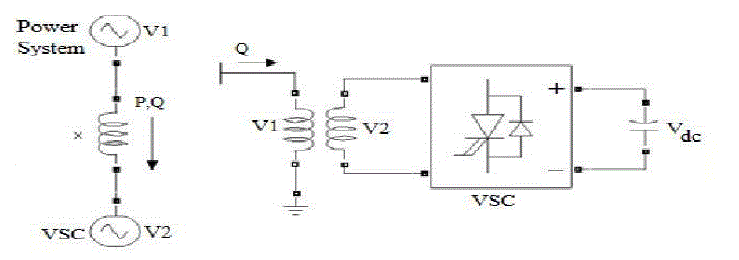
C. Operating Principle of the STATCOM
The operating principle of STATCOM is explained in the figure.1 showing the active and reactive power transfer between a power system and a VSC. In this figure, V1 denotes the power system voltage to be controlled and V2 is the voltage produced by the VSC. During steady state working condition, the voltage V2 produced by the VSC is in phase withV1 (i.e.=0), so that only reactive power is flowing (Active power P=0). If the magnitude of voltage V2produced by VSC is less than the magnitude of power system voltage V1, reactive power Q is flowing from power system to VSC (STATCOM is absorbing reactive power mode).
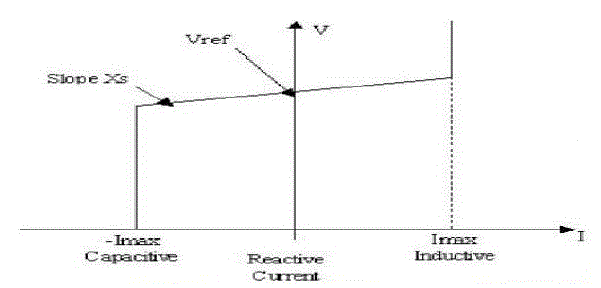
D. STATCOM V-I characteristic
Voltage regulation mode
VAR control mode
When the STATCOM is worked in voltage regulation mode, it implements the V-I characteristic as shown in Fig. 7.The V-I characteristic is depicted by the following equation: Where V= Positive sequence voltage (p.u) I = Reactive current
(I > 0 indicates an inductive current and I< 0indicates capacitive current)
Xs = Slope (p.u. /Pnom : usually between 1% and 5%) Pnom =Converter rating in MVA
In this scheme, each node with message searches for possible path nodes to copy its message. Hence, possible path nodes of a node are considered. Using NSS, each node having message selects its path nodes to provide a sufficient level of end-to-end latency while examining its transmission effort. Here, it derives the CSS measure to permit CRNetworks nodes to decide which licensed channels should be used. The aim of CSS is to maximize spectrum utilization with minimum interference to primary system. Assume that there are M licensed channels with different bandwidth values and y denotes the bandwidth of channel c. Each CR-Networks node is also assumed to periodically sense a set of M licensed channels. Mi denotes the set including Ids of licensed channels that are periodically sensed by node i. suppose that channel c is periodically sensed by node i in each slot and channel c is idle during the time interval x called channel idle duration. Here, it use the product of channel bandwidth y and the channel idle duration x, tc = xy, as a metric to examine the channel idleness. Furthermore, failures in the sensing of primary users are assumed to cause the collisions among the transmissions of primary users and CR-Networks nodes.

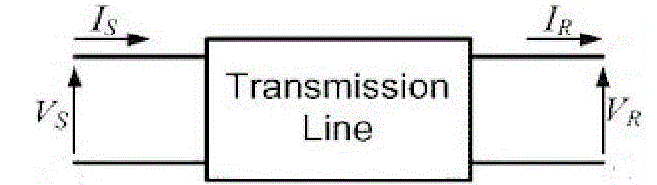
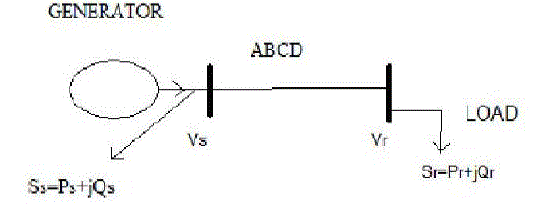
IV.TRANSMISSION LINE MODEL
In this paper, the transmission line is modelled by a two port, four terminal networks as Shown in Figure 3.Transmission lines are operated with a balanced three phase load; the analysis can therefore proceed on a per phase basis. A transmission line on a per phase basis can be regarded as a two port network, where in the sending end voltage and current are related to the receiving end voltage and current through ABCD constants as
The ABCD constants of a line of length l, having a series impedance of z Ω km and shunt admittance of y S km are given by
A=D=cosh( γl) B=ZC sinh(γl) C = sinh(γl) (8)
Where, ZC=zy γ=zy ZC=Characteristic impedance of the line γ=Propagation constant of the line z=series impedance/unit length/phase y =shunt admittance/ unit length/phase to neutral l=transmission line length α=attenuation constant β=phase constant γ =Propagation constant of the line z=series impedance/unit length/phase.
A. Power flow through a transmission line for a actual line model
The principle of power flow through a transmission line is illustrated through a single transmission line (2- node/2-bus system).Let us consider receiving-end voltage as a reference phasor ( V ∟0) and let the sending end voltage lead it by an angle δ is known as the torque angle
The complex power leaving the RE and entering the SE of the transmission line can be expressed as
Sr=Pr+Qr=Vrlr*
Ss=Ps+Qs=Vsls
It is clear from the RE power reaches the maximum value when the angle δ becomes β. However, the SE power becomes maximum at δ = (Π− β). In this study, a 345 kV single circuit transmission line (450 km in length), is considered. It is assumed that each phase of line has a bundle of 2 conductors of size one million c-mils each and conductors are fully transposed. The series impedance and shunt admittance of the line are found to be Z= (0.02986 + j0.2849) Ω/km and Y = j3.989 ×106 S/km, respectively, at 50 Hz. The parameters are obtained using the MATLAB /SIMULINK software. The results of the line are presented in p.u. on a 100 MVA, 345 kV.
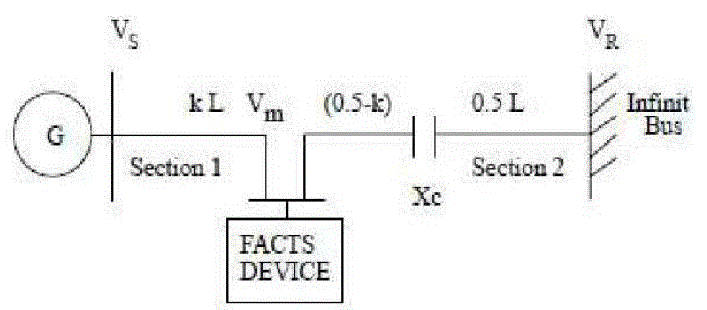
Consider that the line is transferring power from a large generating station to an infinite bus and equipped with series capacitor at centre and a shunt FACTS device at point ‘’m’’ as shown in Figure 10. Parameter k is used to show the fraction of the line length at which the FACTS device is placed. The shunt FACTS device are SVC and STATCOM and is usually connected to the through a step-down transformer. The transmission line is divided into 2 sections (1 & 2), and section 2 is further divided in subsections of length [(0.5−K) & half-line length]. Each section is represented by a separate 2-port, 4-terminal network (similar to Figure 10) with its own ABCD constants considering the actual line model

IV. RESULT AND DISCUSSION
For a simplified model, when there is no FACTS device connected to the line, maximum power transfer through the line is given by [3]: Many researchers established that the optimal location of shunt FACTS device for a simplified model is at K= 0.5 when there is no series compensation in the line. For such cases maximum power transmission capability and maximum transmission angle become double.
However, for an actual line model power flow is given by the above results may not be considered accurate. One of the objectives of this paper is to find the maximum power and corresponding location of shunt FACTS device for different series compensation levels (%S) located at the centre of the line. A sophisticated computer program was developed to determine the various characteristics of the system of Figure 2 using an actual model of the line sections. The constant of the same RE power of section (1) and SE power of section (2) ( 1= 2 ) is included into the problem. In all cases,1.0 p.u. unless specified. The maximum power and corresponding angle are prior determined for various values of location (K).
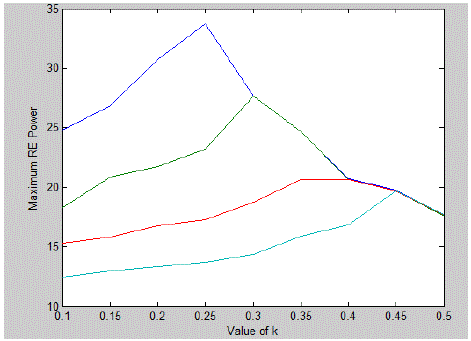
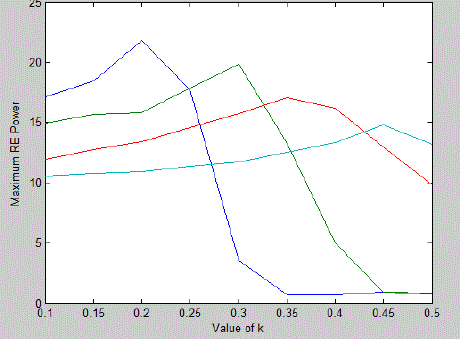
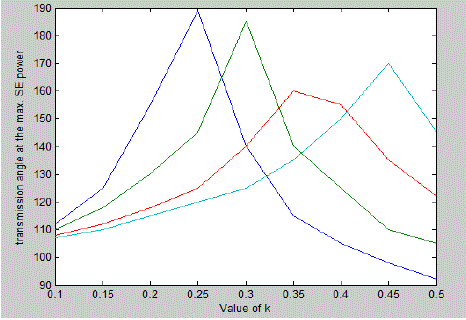
Thus, to get the highest benefit in terms of maximum it means that when series compensation level (%S) is increased then the optimal location of the shunt device shifts towards the generator side. Similarly when %S = 30 then the optimal location is at K = 0.3 and for %S = 45 it is at K = 0.25. Figure 9 shows the variation in optimal off centre location of the shunt FACTS device against the degree of series compensation level (%S) for given R/X ratio of line.

VI. CONCLUSION
This paper investigates the effect of series compensation on the optimal location of a shunt FACTS device to get the highest possible benefit of maximum power transfer and system stability. Various results were found for an actual line model of a series compensated 345 kV, 450 km line. It has been found that the optimal location of the shunt FACTS device is not fixed as reported by many researchers in the case of uncompensated lines but it changes with the change in degree of series compensation. The deviation in the optimal location of the shunt FACT device from the centre point of line depends upon the degree of series compensation and it increases almost linearly from the centre point of the transmission line towards the generator side as the degree of series compensation (%S) is increased. Both the power transfer capability and stability of the system can be improved much more if the shunt FACTS device is placed at the new optimal location instead of at the mid-point of the line. The effect of SVC and STATCOM controllers in enhancing power system stability has been examined. Though both the devices can provide extra damping to the system, it has been demonstrated that STATCOM is very effective in enhancing system performance in situations where system voltages are very much depressed. Also, because of its fast response time, STATCOM control is superior to that of SVC.
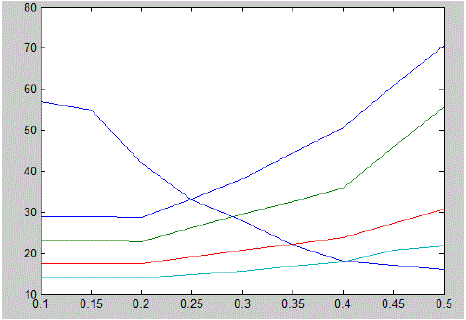
It can be observed in Figure 9 that the optimal off-centre location is 10% for the uncompensated line. When series compensation level (%S) is increased than optimal off-centre location increases linearly and reaches its highest value 55% for %S = 45. Operation of the UPFC demands proper power rating of the series and shunt branches. The rating should enable the UPFC carrying out pre-defined power flow objective.

Figures at a glance




Figure 1 Figure 2 Figure 3 Figure 4 Figure 5
Figure 1 Figure 2 Figure 3 Figure 4 Figure 5
Figure 6 Figure 7 Figure 8 Figure 9 Figure 10
Figure 6 Figure 7 Figure 8 Figure 9 Figure 10
Figure 11 Figure 12 Figure 13 Figure 14
Figure 11 Figure 12 Figure 13 Figure 14
 

References