Research and Reviews - International Journals

International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Menu

ISSN ONLINE(2278-8875) PRINT (2320-3765)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

OPTIMAL POWER FLOW USING CUCKOO OPTIMIZATION ALGORITHM

M.RamaMohana Rao1, A.V.Naresh Babu2
  1. PG Student [P.E], Dept. of EEE, DVR &Dr. HS MIC College of Technology, Andhra Pradesh, India
  2. Associate professor, Dept. of EEE, DVR &Dr. HS MIC College of Technology, Andhra Pradesh, India
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Abstract

This paper presents an efficient and reliable evolutionary-based approach to obtain optimal power flow (OPF) problem solution. The approach employs a nature inspired meta heuristic optimization algorithm called cuckoo optimization algorithm (COA) to determine the optimal settings of control variables. The performance of the COA is examined and tested on IEEE 14 bus test system with fuel cost minimization as objective function. The results demonstrate the potential of the COA shows its effectiveness and robustness to solve the OPF problem.

Keywords
Cuckoo optimization algorithm, optimal power flow, optimization techniques, cost minimization, power systems.

I.INTRODUCTION
Optimal power flow (OPF) has become one of the most important problem and it is the fundamental tool that enables electric utilities to specify economic operating and secure states in power systems. The main objective of the OPF problem is to optimize a chosen objective function such as fuel cost, piecewise quadratic cost function, fuel cost with valve point effects, voltage profile improvement, voltage stability enhancement, through optimal adjustments of power systems control variables while at the same time satisfying system operating conditions with power flow equations and inequality constraints. The equality constraints are the nodal power balance equations, while the inequality constraints are the limits of all control or state variables. The control variables involves the tap ratios of transformers, the generator real power, the generator bus voltages and reactive power of sources. In general the OPF problem is a large-scale, highly constrained, nonlinear and non-convex optimization problem.
The OPF problem has been solved by using traditional and evolutionary based algorithms. In the past conventional methods were employed for the solution of OPF problem. H.W.Dommel and W.F.Tinney[1] firstly presented the solution of optimal power flow. Conventional optimization techniques such as interior point method, linear programming and nonlinear programming have been discussed by K.Deb [2]. However the disadvantage of these techniques is that it is not possible to use these techniques in practical systems because of nonlinear characteristics such as valve point effects, prohibited operating zones and piecewise quadratic cost function. Therefore it becomes necessary to improve the optimization methods that are capable of overcoming these disadvantages and handling such difficulties. Recently many population based optimization techniques have been used to solve complex constrained optimization problems. These techniques have been increasingly applied for solving power system optimization problems such as economic dispatch, optimal reactive power flow and OPF for decades.
Some of the population-based methods have been proposed for solving the OPF problem successfully such as genetic algorithm(GA), particle swarm optimization(PSO), differential evolution(DE), simulated annealing(SA), Intelligent search evolutionary algorithm(ISEA) etc., Then the topic has been handled by many researchers. R.Gnanadass et al. [3] is devoted an evolutionary programming algorithm to solve the optimal power flow problem with non-smooth fuel cost functions. M.R.AlRashidi and M.E.EI.Hawary [4] has reported a hybrid particle swarm optimization algorithm as a modern optimization tool to solve the discrete optimal power flow problem with valve loading effect. M.Varadarajan and K.S Swarup [5] presented differential evolution approach to solve optimal power flow problem with multiple objectives. A.V.NareshBabu and S.Sivanagaraju [6] proposed a new approach based on two step initialization to solve the OPF problem. Different methods to find the solution for OPF problem has been discussed in [7-9]. One of the recently proposed meta heuristic algorithm is the cuckoo optimization algorithm was proposed in [10-12]. It is based on the intelligent breeding behaviour of cuckoo. In this paper, COA is used to solve the OPF problem which is formulated as a nonlinear optimization problem with equality and inequality constraints in a power system. The objective function is to minimize the fuel cost. The performance of the proposed approach is sought and tested on the standard IEEE 14 bus test system. Obtained simulation results demonstrate that the COA provides very remarkable results for solving the OPF problem.

II.MATHEMATICAL PROBLEM FORMULATION OF OPF
The OPF is a nonlinear optimization problem. The essential goal of the OPF is to obtain the optimal settings of control variables in terms of a certain objective function subjected to various equality and inequality constraints. In general, the OPF problem can be mathematically formulated as follows:
Min f(x,u) (1) Subject to g(x,u) = 0
h(x,u) ≤ 0
Where f is the objective function to be minimized, x and u are vectors of dependent and control variables respectively. x is the vector of dependent variables including:
Generator active power input at slack bus Pg1
Load bus voltage Vl.
Generator reactive power input Qg.
x can be represented as:
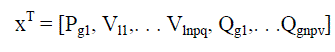image (2)
wherenpvandnpq defines the number of voltage controlled buses and number of PQ buses respectively. In a similar way the vector of control variables u can be expressed as:
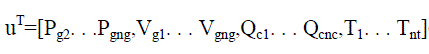image (3)
Pg defines the active power output of generators at PV bus.
Vg depicts the terminal voltages at generation bus bars.
Qc represents the output of shunt VAR compensators
T stands for the tap setting of the tap regulating transformers.
wherent and nc define the number of tap regulating transformers and number of shunt VAR compensators, respectively
A.Objective function
The minimization of fuel cost is considered as an objective function to examine the performance of COA. The aim of the fuel cost minimization is to determine optimal generation settings of thermal generating units which minimize the total fuel cost while satisfying all the equality and inequality constraints. The total fuel cost function (J) for a number of thermal generating units can be represented by a quadratic function as
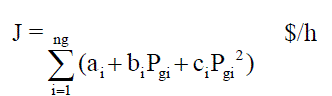image (4)
Where ai, bi& ci are cost coefficients of ith generator.
Pgi is the generation at ith generator
ng is the number of generator buses.

III.CUCKOO OPTIMIZATION ALGORITHM
A. Overview
The cuckoo optimization algorithm (COA) is a nature inspired meta heuristic algorithm which is inspired by the life of a bird family, called Cuckoo. Special lifestyle of these birds and their characteristics in egg laying and breeding has been the basic motivation for development of this new evolutionary optimization algorithm. It is a novel evolutionary algorithm, suitable for continuous nonlinear optimization problem.
Similar to other evolutionary methods, COA also starts with an initial population. The effort to survive among cuckoos constitutes the basis of cuckoo optimization algorithm. During the survival competition some of the cuckoos or their eggs may demise. The survived cuckoo societies immigrate to a better environment and start reproducing and laying eggs. Cuckoos survival effort hopefully converges to a state that there is only one cuckoo society, all with the best profit values. Application of the COA algorithm to some benchmark functions and a real problem has proven its capability in solving complex, nonlinear and non-convex optimization problems.
The key features of the COA are faster convergence rate and reduction in computational complexity. Similar to other evolutionary algorithms, it is also a population based algorithm. The initial population is randomly generated within the control parameter limits. Then the levy flight operator is performed on all individuals until a stopping criterion is reached.
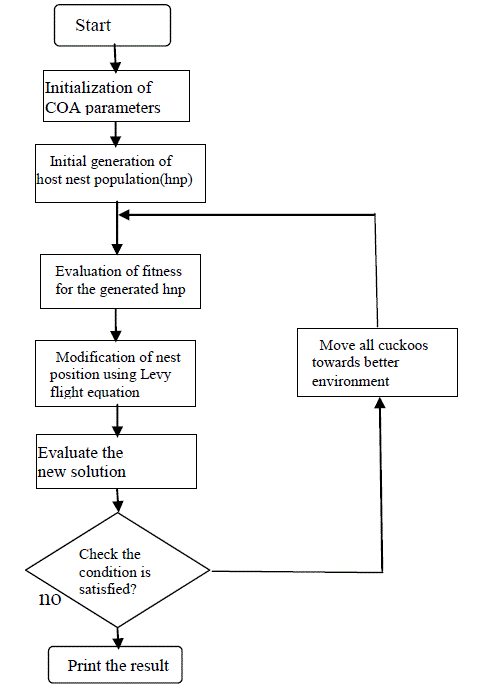
B. Solution methodology of COA
The main steps of COA are shown in Fig.1

IV.NUMERICAL RESULTS
In order to demonstrate the effectiveness and robustness of the COA method to solve the OPF problem, the objective function of fuel cost minimization is applied on IEEE 14 bus system [13] and the results are presented. The method is implemented using MATLAB software on a personal computer with Intel Pentium dual core 2.6 GHz processor and 1 GB RAM. The input parameters of COA for the test system are considered as the number of host nests as 10, Levy flight constants λ as 1≤λ≤3 and α as rand (-1,1). The number of iterations to be 10. Table I summarizes the OPF results. The real power generation and losses are expressed in MW and the cost is in $/h. The bus voltages and corresponding phase angles for fuel cost minimization are given in Table II.
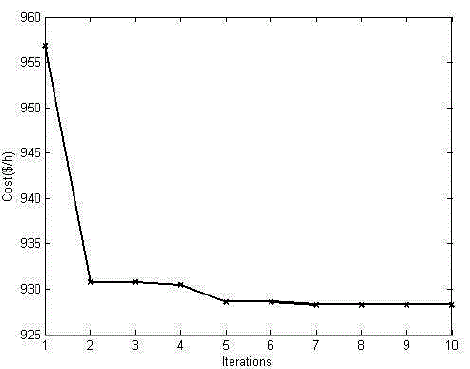
From Table I, it can be observed that the power generation of individual generators, generator voltage, total power generation, total losses and the cost obtained using COA is satisfactory. Table II gives the voltage magnitudes and corresponding phase angles at each bus using COA are better. Fig. 2 indicates the convergence characteristics of the test system using COA. From Fig. 2, it can be observed that the initial cost (at 1st iteration) is 956.881 $/h and it falls to 928.285 $/h ( at 10th iteration) for COA.From this, it can be concluded that the initial cost and change in cost (from 1stiteration to 10th iteration) using COA is less and the fuel cost is minimized in less number of iterations.From this, it is clear that COA gives the converged solution with less number of iterations and it results in reduction of computation time.

V. CONCLUSION
In this paper, one of the recently proposed heuristic algorithm COA is used to solve the optimal power flow problem in powersystems. The OPF problem is formulated as a nonlinear optimization problem with equality and inequality constraints in power systems.In this case theminimization of fuel cost is considered as objective function. This approach was successfully and influentially performedto find the optimal settings of the control variables of test system.The simulation results proved the robustness and superiority of the COA approach to solve the OPF problem. The effectiveness of this algorithm is demonstrated on IEEE 14 bus system. The observations reveals that the COA gives optimal solution with lessnumber of generations and requires less computation time.

Tables at a glance
Table icon Table icon
Table 1 Table 2
 

Figures at a glance
Figure 1 Figure 2
Figure 1 Figure 2
 

References