This paper presents new optimal scheduling technique for charging the batteries of Electrical Vehicles (EVs) where the electric supply companies offer differential pricing depending on the Time-of-Use (TOU). The optimal schedule minimizes the total chargingcost of the battery of a specific EV. At the charging station, the arrival and departure time of the EV is taken into consideration along with the required charging power sequence.
Keywords |
| Arrival time slot, Binary Integer programming, departure time slot, Kronecker product, Linear Sum
Assignment Programming (LSAP), Plug-in Electric Vehicle (PEV), sort index, Time-of-Use pricing,charging
stints,vec-operator. |
I. INTRODUCTION |
| Battery driven Electric Vehicles (EVs) are ecologically superior to conventional fossil fuel driven vehicles. Periodic
charging of the batteries is an important requirement in the operation and maintenance of EVs. Easily accessible and
efficient Charging Stations will boost the usage of EVs. In a smart grid, the Time-of-Use (TOU) pricing of electricity
scheme [1], [2] is a Demand Side Management (DSM) technique.Here, the electrical energy is differentially priced
depending on the time of use in a day. The energy cost is priced at a higher rate during peak demand hours so that users
are encouraged to consume more during lean periods. This will, to some extent, make way for over all uniform load
distribution.In those places where the electricity market is highly regulated and the TOU pricing is adopted, it is
possible to schedule the charging task to minimize the total cost of electricity used to charge the battery of the EV in
the specified duration. The objective of this paper is to calculate the optimum charging schedules to minimize cost of
electricity used under different charging constraints.Several solutions have already been proposed for optimum
charging of EV batteries based on different techniques [3], [4], [5]. A game theoretic approach is used in [6]. |
II. TIME-OF-USE PRICING, ASSUMPTIONS AND NOTATIONS |
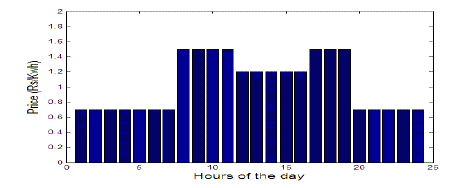
| A typical 24 hour TOU price information is shown in the bar graph of Fig.1. Normally the TOU tariff will be different
for weekdays and holidays/weekends. In general, the TOU price varies on hourly basis during the 24 hour day. For
convenience, the 24 hours of the day are divided into 24 standard slots of one hour each. The TOU time slots are
sequentially numbered as j = 1, 2,…, 24. Slot 1 starts just after midnight(00 hrs) and occupies the time interval from 00
to 01 hrs. Slot i occupies the time interval (i–1) to i hrs. |
| For a given TOU scheme, the unit price (rate) information is stored in the array R(j) for j = 1, 2,…,24. Here, R(j) is the
price of the electrical energy in time slot j. Variable j represents the time slot index for the Ncontiguous hours of the
day under consideration. Since TOU pricing is generally cyclic with a 24 hour period, it repeats itself after every 24
hours except for holidays and weekends. Therefore R(j) is periodic as, |
| R(j+24) = R(j) (1) |
| Thus the price matrix is R = [R(1) R(2) … R(24)]. The size of R is (1, 24). It is a row vector. In some situations, all the
24 hours may not be available for charging. Therefore we may take the range of the price vector R fromR(1) to R(N).
That is, R = [ R(1) R(2) …. R(N)]. Invariably N=24. Therefore in our discussion we take N=24. |
| A. Charging Sequence |
| In this section, we consider the charging of one EV battery. To take advantage of the TOU pricing, we would like to
charge the battery during the low price time slots as far as possible and to skip charging during high price time slots.
Thereforethe charging of the battery will be intermittent (in burst). Thus we use ON-OFF charging. The battery
charging ON-OFF time periods are also expressed in terms of the standard time slots adopted to describe TOU pricing.
Thus an ON or OFF charging intervals will be an integers representing the hours of the day. The ON charging
operation for aninterval of one hour is calledacharging stint. The charging stints are synchronous with the time slots of
the day. That is, the starting and ending of a charging stint coincides with that of a time slot. A typical charging
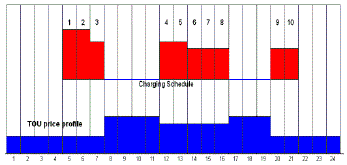
sequence is shown in Fig.2. |
| In Fig. 2, the charging operation has 10 charging stints. The charging stints are sequentially marked as,1, 2, 3, (fourgaps)
4, 5, 6, 7, 8, (three-gaps) 9, 10. In general, let the total number of charging stints in a charging cycle be M. The
individual stints are designated as i = 1, 2, …, M.Normally M is less than or equal to 24 so that a charging cycle has a
duration less than or equal to 24 hours. |
| B. Power and Energy Drawn by the battery. |
| Let the charging power drawn by the concerned EV battery in its successive charging stints (time periods)be
represented by P(i)’s for i = 1, 2,…, M. The unit of P(i) is in Kilowatts. Here, P(i)’s represent the battery charging
power sequence. The total charging energy E, in Kilowatt hours, drawn by the battery in one charging cycle would be, |
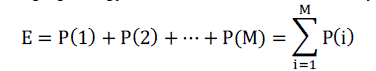 (2) (2) |
| The charging power sequence is represented by the row matrix P = [P(1) P(2) … P(M)]. The size of P is (1, M). |
| C. Arrival and departure time of the EV |
| We assume that the battery of the EV is available for charging as soon as the EV arrives at the charging station. Let
the EV arrive at the charging station at T1 hrs. IfT1isat the beginning of the time slot J, then the arrival slot,designated
as a,is taken as J. If t1 is somewhere in the middle of the time slot J, then a is taken as (J+1). That is the arrival time slot
a is given by, |
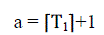 (3) (3) |
| Thus if T1 = 01.30 hrs, it has arrived in the middle of time slot 2. Therefore a = 3. The departure slot b corresponding to
the departure time T2hrs, is given by, |
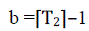 (4) (4) |
| Thus if T2 = 12.30 hrs, then b = 12. The charging operation can take place between a andb as shown in Fig. 3. Here, the
available slots for charging are from a tob.That is from 3 to 12. In Fig. 3, the time slots are marked in red numbers. If
the departure time belongs to the next day, add 24 to T2 to get the effective T2.Since the first slot available for charging
is a, the first charging stint x(1) can be a or greater than a. Similarly, the last charging stint can occur on or before b.
Thusx(1) ≥ aand x(M) ≤ b. That is, |
| a ≤ x(i) ≤ b (5) |
| Since we have M charging stints, they should occur within the range a tob. Therefore the total number of available time
slots should be greater than or equal to M. That is, |
| (b–a+1) ≥ M (6) |
| In oursolution, we assume that the condition specified by Eq.(6) is satisfied |
| D. Charging Schedule |
| = 5.) Let the charging power in stint 1 beP(1). Therefore the power P(1) is drawn in the time slot x(1). Let the second
charging stint be at time slot x(2). (In Fig. 2, x(2) = 6.) Naturally x(2) >x(1) because, the second stint occurs after the
first one. There may be gaps between x(2) and x(1).Power drawn during x(2) is P(2). Similarly the i th charging stint
occupies the time slot x(i). The time slots occupied by the consecutive charging stints are represented by x(1),
x(2),…,x(M). The charging powers drawn are, |
| P(1) during day time slot x(1) |
| P(2) during day time slot x(2)
………………………………… |
| P(i) during day time slot x(i)
………………………………… |
| P(M) during day time slot x(M) |
| Thus the power drawn for charging in slot x(i) is P(i) for i =1,2, 3,…, M. The sequence x(i) for i = 1 to M forms the
charging schedule. Thus the charging schedule denoted by symbol X is, |
| X = [ x(1), x(2), … x(i),…, x(M)] (7) |
| In Fig.2, the charging schedule X is, |
| X=[ 5, 6, 7, 12, 13, 14, 15, 16, 20, 21] |
| The charging energy during charging stint i of 1 hour duration is P(i)*1=P(i).This P(i) occurs in the time slot x(i). The
energy price in slot x(i) is given by R(x(i)). Therefore the corresponding charging cost would be R(x(i))*P(i). Hence
the total cost for all the stints is, |
| C = R(x(1))*P(1)+R(x(2))*P(2)+,…+R(x(M))*P(M) |
| That is, |
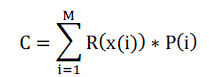 (8) (8) |
| Here, our objective is to minimize C by properly choosing the sequence ofx(i)’s. |
III. CONSTRAINED OPTIMIZATION |
| Optimal battery charging schedule is to determine the sequence x(i) for i = 1 to M to minimize C as given by Eq. (8).
The following data are given. |
| 1. Number of TOU time slots N. |
| 2. Number of charging stints M. |
| 3. TOU pricing scheme represented by R(j) for j = 1 to N. |
| 4. Battery charging power sequence P(i) for i = 1 to M. |
| 5. Arrival and departure timesT1 and T2of the EV. Thus a and b are known. |
| While determining the sequence x(i) for i = 1 to M, the following constraints are to be satisfied. |
| 1. x(i)∈{1 to N} for i = 1, 2,..., M (9) |
| 2. x(i+1) > x(i) for i=1, 2,..., (M–1) (10) |
| 3. a ≤ x(i) ≤ b (from Eq. (5) ) (11) |
| A. Solution |
 |
| Therefore, the minimum of D is, |
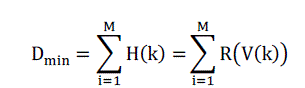 (23) (23) |
| Hence, the indices of R’s which minimize F are given by V(k) = a+Q(k)–1 for k = 1 to M. Thus x(i)’s belong to the set
{V(k) for k = 1 to M}. Since x(i)’s have to be a sequence in the ascending order, x(i)’s are obtained by sorting V(k)’s in
the ascending order. Thus the optimal sequence S is given by, |
| S = [ x(1), x(2), … x(i),…, x(M)]=sort(V) (24) |
| The above process of determining the optimal sequence S is described in Algorithm 1. |
| Algorithm 1.The inputs are: TOU price sequence R(j)’s. The lowerand upper limits a and b on x(i)’s. |
| Output: Optimal sequence S =[ x(1), x(2), … x(i),…, x(M)]. |
| 1. Get the sequence G using Eq. (13). |
| 2. Sort G in the ascending order to get H and the sort_index using Eq. (17). |
| 3. Get Q, the first M terms of G using Eq. (19). |
| 4. Add offset (a–1) to the elements of Q to get V as,
V(k) = Q(k)+ a–1 for k = 1 to M |
| 5. Get X by sorting array V in the ascending order as, X = sort(V). |
| 6. Get Dmin using Eq. (23). |
 |
| In the light of Eqs. (27), Eq. (26) becomes, |
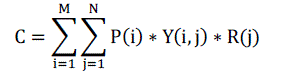 (28) (28) |
| Here Y(i, j) is the element at row i and column j of the binary matrix Y. The size of Y is(M, N).When Y(i, j) =1,
charge stint i is assigned to the time slot j. Then P(i)*Y(i, j)*R(j) =P(i)*R(j) represents the cost of charging with stint I
assigned to slot j. To choose Y(i, j) to Minimize C given by Eq. (26) is a Linear Sum Assignment Problem(LSAP) [4].
We have to assign appropriate charging stint i to the TOU time slot j so that C is minimum.
Eq.(28) can be written in the matrix form as, |
| C = P*Y*RT (29) |
| where P =[ P(1) P(2) … P(M)] is a row matrix of size (1, M) and R = [R(1) R(2) … R(N) ] is the price matrix of
size (1, N). |
| D. Constraints of the LSAP |
| In our assignment problem, charging stint i should be assigned to a single time slot. Therefore, |
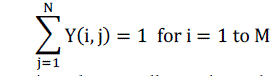 (30) (30) |
| When the arrival and the departure time slots a andb are given, the summation range of Eq. (28) for j would be from j
= a to b. No assignments are made outside this range. Therefore, the summation terms are zeros outside this range.
Hence Y(i, j) = 0 outside this range. Therefore Eq. (30) is modified as, |
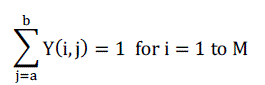 (31) (31) |
| This means only one element of each array Y(i, j) for j =a to b has to be 1 and the remaining elements have to be
zeros.From Eq. (28), the time slot assigned for charge stint i is, j = x(i). Therefore, |
| Y(i, j) = 1 when j = x(i) |
| and Y(i, j) = 0 when j ≠ x(i) |
| for i =1 to M. |
| The above condition is expressed as, |
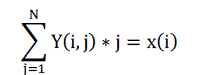 (32) (32) |
| Now for row (i+1), the above equation becomes, |
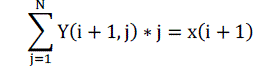 (33) (33) |
| We know from Eq. (10), that x(i+1) > x(i). This means, the column locations of 1’s should progressively increase as we
go from the present row to the next row. Therefore, from Eqs. (10), (32) and (33), |
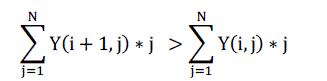 (34) (34) |
| Eq. (34) should hold good for i =1 to (M–1). |
| Thus the LSAP is to determine Y to minimize C given by Eq. (30), subjected to the conditions of Eqs. (31) and (34).
Another important constraint is, a TOU time slot cannot accommodate more than 1 battery charging stints. We assume
that a single battery is gettng. It can be one or none. |
| This constraint can be formulated as, |
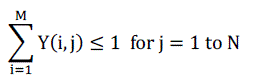 (35) (35) |
| E. Column Major format of Y or vec(Y) |
| The optimization problem is to determine the binary matrix Y to minimize C given by Eq. (29). Determination of Y
is easy if Y is in the column major or single column format. The column major format of Y is obtained by arranging the
columns of Y one beneath the other. This result is obtained using the vec-operator [7] as follows. |
| Let Y = [ Z(1) Z(2) … Z(j) … Z(N) ] |
| where Z(1), Z(2),…, Z(j),… Z(N) are the columns of Y. |
| Then vec(Y) is defined as, |
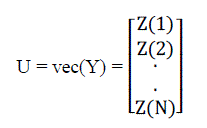 (36) (36) |
| The vec-operator vectorizes the matrix. The well known theorem [9] using vec-operator states that, |
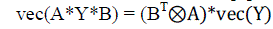 (37) (37) |
| For compatible size matrices A, Y and B. In eq(37), is the Kronecker product [9] operator. |
| From Eqs. (29), (36) and (37), |
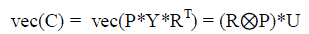 (38) (38) |
| Since C is a scalar, vec(C) = C itself. Therefore the cost of charging C is, |
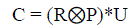 (39) (39) |
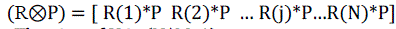 (40) (40) |
 |
 |
 |
| F. Recovering Y from U |
| From the optimal U, the equivalent optimal binary matrix Y of size (M, N) is recovered using the reshape [9] function
as, |
| Y = reshape(U, M, N) (72) |
| The reshape function returns the M-by-N matrix Y whose elements are taken column-wise from U.
The locations of 1 in Y give the allocation of charging stints to the respective TOU time slots. If Y(I, J) =1, it means the
charging stint I allocated to the time slot J. That is, the row index represents the charge stint and the column index
represents the TOU time slot. |
| The optimal allocation time slots x(1) , x(2),...,x(M) are determined by finding the column locations of 1’s in Y for
the successive row locations. This is done using the Matlabfind function as, |
| [ I J] = find(Y) (73) |
| Here the subscript set[ IJ ] gives the locations of 1’s in Y. Column vector I gives the row index and the column vector J
gives the corresponding column index of 1’s in Y. The size of J is (M, 1). The contents of I will be from 1 to M. The
optimum charging schedule is given by, |
| X = [ x(1), x(2), … x(i),…, x(M)] = JT (74) |
| JT is the transpose of J. |
IV. OPTIMAL SCHEDULING ALGORITHM |
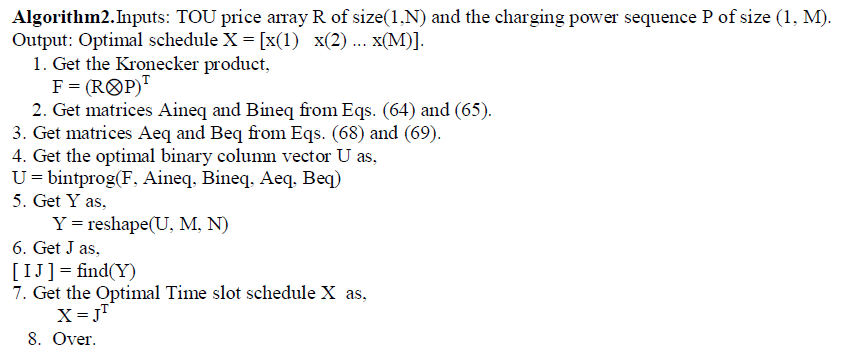 |
V. RESULTS & DISCUSSION WITH EXAMPLES |
| Example 1:TOU price sequence is given in TABLE 1. The price is in some appropriate units. Charging Power is
constant.TABLE 1. TOU price information for 24 time slots |
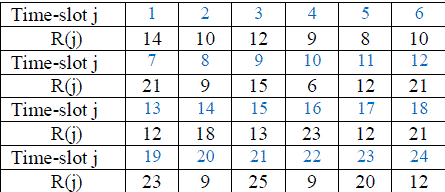 |
| The arrival and departure time slots are, a = 3 and b = 12. The number of charging stints are M = 7.
From Eq. (13), |
 |
 |
VI. CONCLUSION |
| A Binary Integer Programming approach is presented for minimizing the EV battery charging cost under the
differential Time-of_Use (TOU) price scheme. In this paper the TOU time slot interval is takenas 1 hour. Our method
holds good for different values of the time slot interval either higher or lower granularity. |
Figures at a glance |
 |
 |
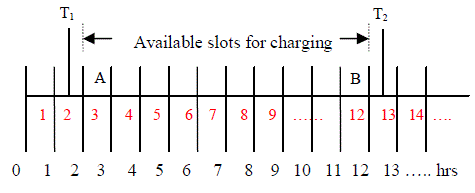 |
| Figure 1 |
Figure 2 |
Figure 3 |
|
| |
References |
- C. W. Gellings, “The concept of demand-side management for Electricutilities,”Proc. IEEE , vol. 73, pp. 1468–1470, 1985.
- S. Rahman and SR. Rinaldy, “An efficient load model for analyzingdemand side management impacts,”IEEE Trans. Power Syst.vol. 8, pp. 1219– 1226, 1993.
- S.Deilami, A. S. Masoum, P. S.Moses, and M. A. S. Masoum, “Realtimecoordination of plug-in electric vehicle charging in smart grids tominimize power losses and improve voltage profile,” IEEE Trans. Smart Grid, vol. 2, no. 3, pp. 456–467, Sep. 2011.
- J. A. Peças Lopes, F. J. Soares, P. M. Almeida, M. Moreira da Silva“Smart Charging Strategies for Electric Vehicles: Enhancing GridPerformance and Maximizing the Use of Variable Renewable Energy Resources,” 24th International Electric Vehicle Symposium andExposition (EVS24) InProceedings 24th International Electric Vehicle Symposium and Exposition (EVS24) (May 2009), pp. 1-11.
- D. T. Phan, JinjunXiong, S. Ghosh“A distributed scheme for fair EV charging under transmission constraints,”2012 American ControlConference (ACC) Proceedings In 2012 American Control Conference (ACC) Proceedings (June 2012), pp. 1053-1058.
- W. Tushar, W. Saad, H. V. Poor, D. B. Smith, “Economics of Electric Vehicle Charging: A Game Theoretic Approach,” IEEE Transactions onSmart Grid In IEEE Transactions on Smart Grid, Vol. 3, No. 4. December 2012, pp. 1767-1778.
- M. Akg¨ul, “The linear assignment problem, in Combinatorial Optimization,” M. Akg¨uland S. Tufecki, eds., Springer Verlag, Berlin, 1992, pp.85–122.
- Rainer E. Burkard, ErandaC¸ela, “Linear Assignment Problems and Extensions,” Handbook of Combinatorial Optimization: Supplement,Volume 1. Ding-Zhu Du, Panos M. Pardalos. Springer, Oct 31, 1999.
- Jan R. Magnus and Heinz Neudecker (1999), Matrix Differential Calculuswith Applications in Statistics and Econometrics, 2nd Ed., Wiley. pp.31-35.
|