This article deals with an application of Particle Swarm Optimization (PSO) to obtain a optimum PI controller settings for a non linear process. In this work, a conical tank level process is identified as first order plus dead time model (FOPTD). Control of level in conical tank is a complex issue but in the presence of gravity discharge flow conical tanks are used in industrial unit. PSO algorithm is used to tune the parameters of PI controller to control the level of the liquid in the conical tank. Efficacy of proposed method has been validated through a comparative study with gain scheduling method. The proposed method has excellent features of high computational efficiency. In this paper optimum values of PI controller settings are found and it is proved that the PSO based tuned PI values gives better results than the gain scheduling method. Hence the results demonstrates that the tuning of PI controller using PSO technique gives minimum rise time, minimum settling time than Gain Scheduling method and also reduces the IAE.
Keywords |
| PSO, Computation Intelligence, Gain Scheduling, PI Controller, Non Linear Process |
I. INTRODUCTION |
| Role of PID controller in industries have been found more than fifty years [1]. Over the past 50 years research work on
PID tuning methods are carried out which includes Ziegler-Nichols Ultimate-cycle tuning [1], Cohen-Coon’s [2],
Astrom and Hagglund [3] and many other techniques are also emerged. Since PID control has been an energetic
research topic. PID controllers were widely used in many process plants; it gives satisfactory output from minimum
plant information. These technique is highly appreciated by many researchers [6,8] because of the adjustments will be
made in controller parameters with minimum attempt. PID controller must be properly tuned to get the desired
response. Tuning a PID controller means setting the proportional, integral and derivative gain values to get the best
possible control for a particular process. |
| In past few decades, to meet system demands researchers were deals with intelligent agents claiming that its a central
ability of humans, intelligence [4, 5]. Owing the complexity in their real time implementation and tuning, the research
community as well as the industrial to pay attention towards computation intelligence [9-11]. The computation
efficiency is the advantage of particle swarm optimization algorithms over other tuning techniques. |
| Particle swarm optimization (PSO) is a computational algorithm technique based on swarm intelligence. This method is
motivated by the observation of social interaction and animal behaviours such as fish schooling and bird flocking. It
imitates the way they find food by the cooperation and competition among the entire population [7]. A swarm consists
of individuals, called particles, each of which represents a different possible set of the unknown parameters to be
optimized. The ‘swarm’ is initialized with a population of random solutions [9]. In a PSO system, particles fly around
in a multi-dimensional search space adjusting its position according to its own experience and the experience of its
neighbouring particle. The goal is to efficiently search the solution space by swarming the particles towards the best
fitting solution encountered in previous iterations with the intention of encountering better solutions through the course
of the process and eventually converging on a single minimum or maximum solution [10]. The performance of each
particle is measured according to a pre-defined fitness function, which is related to the problem being solved.
The accuracy of the tuned controller is greatly dependent on the degree of accuracy of the system model. So the model
of the process much more important. Analysis show that the design of proposed controller gives a better robustness,
and, the performance is satisfactory over a wide range of process operations[12].Simulation results describes the efficiency of the PSO based PI controller in point of improvement of performances in time domain specifications for a
step response with that of gain scheduling algorithm. |
| The objective of the proposed work is to use Particle swarm optimization in order to obtain optimal values for PI
controller parameters for a conical tank process. The dynamic behavior of a conical tank level system is high degree of
non-linearity, and parameter is time variances in these processes make it extremely difficult to control. To overcome
the problem of non linearity, the process must be linearized i.e. full range is sliced into linear regions. Hence we
propose four set of PI parameters. Every possible controller setting represent a particle in the search space which
changes its parameters proportionality constant, Kp, integral constant, Ki, in order to minimize the error function and in
this case error function is taken as objective function. The error function used here is Integral of Absolute errors
(IAE).In section 2, we have discussed in detail about the development of the mathematical model for the non-linear
conical tank process. The tuning results of conventional techniques are discussed in section 3. Section 4 and 5 deal with
the explanation of the PSO algorithm and its implementation. The comparative analysis and results are given in Section
6. The conclusions arrived, based on the results is given in Section 7. |
II. MATHEMATICAL MODELING |
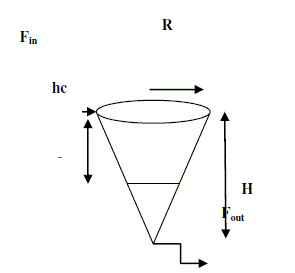
| The conical tank system shown in Figure1 is a system with nonlinear dynamics. Its nonlinearity is described by the
differential equation [14]. |
| It is derived according to law of conservation of mass, |
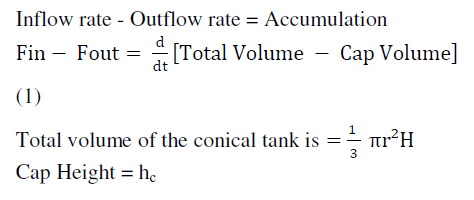 |
| By solving equation 1 we get, |
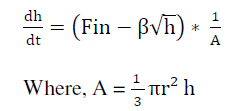 (2) (2) |
| The equation [2] describing the mathematical model for single conical tank level control, this equation is implemented
in MATLAB Simulink. The basic method of identifying the system is step response method. A step change in inlet
flow rate represents a process as first order transfer function with dead time. |
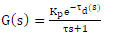 (3) (3) |
| Where K is the process gain; τ is the first order time constant; τd is the dead time (1 sec). Due to the non-linearity in the
shape of the conical tank, a single range response cannot cover the entire range. So, full range of conical tank is sliced
into different regions by introducing step change at various ranges, four responses were obtained for 0-1.44cm as
model-1, 1.44-5.76cm as model-2, 5.76-12.83cm as model-3 and 12.83-23.04 cm as model-4 with process gain
0.0218, 0.0654, 0.109, 0.155 and time constant 0.041, 0.24, 1.97, 11.75 respectively. |
III. ADAPTIVE CONTROL TECHNIQUE |
| In this paper a gain scheduling approach is discussed. It is a model based approach, PI controller parameter were
identified from the model parameters. In this approach, gain is scheduled with respect to operating regions. This
method has scheduling variable, based upon the scheduling variable PI controller gain values the proportional ( ) and
integral gain ( ) are calculated [14,15]. |
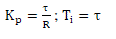 (4) (4) |
IV. PSO BASED PI CONTROLLER |
| A. Particle Swarm Optimization |
| In PSO algorithm, the system is initialized with a population of random solutions, which are called particles, and each
potential solution is also assigned a randomized velocity. PSO relies on the exchange of information between particles
of the population called swarm. Each particle adjusts its trajectory towards its best solution (fitness) that is achieved so
far. This value is called pbest. Each particle also modifies its trajectory towards the best previous position attained by
any member of its neighborhood. This value is called gbest. Each particle moves in the search space with an adaptive
velocity. |
| The fitness function evaluates the performance of particles to determine whether the best fitting solution is achieved.
During the run, the fitness of the best individual improves over time and typically tends to stagnate towards the end of
the run. Ideally, the stagnation of the process coincides with the successful discovery of the global optimum. |
| Let D be the dimension of the search space taken into consideration and Xi = [xi1, xi2,….xiD]T denote the current
position of ith particle of the swarm, Then: Xi pbest =[xi1
pbest,xi2
pbest,….xiD
pbest] T denote the best position ever visited by
the particle.Xgbest =[x i1
gbest,x i2
gbest,….x i2
gbest] T represents ‘gbest’,i.e the best position obtained this far by any particle
in the population. Vi=[v i1,v i2,….v iD] T represents the velocity of ith particle. Vimax = [vi1
max,vi2
max ….viD
max] T denotes
the upper bound on the absolute value of the velocity with which the particle can move at each step.The position and
velocity of the particles is adjusted as per the following equation: |
 (5) (5) |
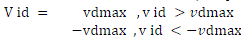 (6) (6) |
 (7) (7) |
| where c1 and c2 are positive constants, represent the cognitive and social parameter respectively; r1 and r2 are random
numbers uniformly distributed in the range [0,1]; w is inertia weight to balance the global and local search ability. In
general the PSO technique can be given by the following algorithm, |
| B. Algorithm |
| Step1: Start the program |
| Step2: Initialize particles with random place and velocity |
| Step3: Evaluate fitness value for each particle |
| Step4: If current fitness value is better than pbest, goto step5 else goto step8. |
| Step5: Pbest equal to current fitness value |
| Step6: If current fitness value is better than Gbest, goto to step7 else goto step 8 |
| Step7: Gbest is equal to current fitness value. |
| Step8: Update position and velocity of particles |
| Step9: Goto step10 if stop criteria met else goto step3. |
V. IMPLEMENTATION OF PSO ALGORITHM |
| The optimal values of the PI controller parameters Kp, Ki are found using PSO. All possible sets of controller
parameter values are particles whose values are adjusted so as to minimize the objective function, which in this case,
the error criterion is discussed in detail. For the PI controller design, it is ensured the controller settings estimated
results in a stable closed loop system. |
| A. Selection of PSO parameters |
| To start up with GA, predefining certain parameters is necessary. It includes the population size, iteration length,
velocity constants etc. Selection of these parameters decides to a great extent the ability of designed controller[13]. The
size of swarm balances the requirement of global optimization and computational cost. Initializing the values of the
parameters is listed in table II. |
| A. Performance Index for the PSO Algorithm |
| The objective function considered is based on the error criterion. The performance of a controller is best evaluated in
terms of error criterion. A number of such error criteria are available and in the proposed work, performance of the
controller’s is examined in terms of Integral of Absolute Errors (IAE) criterion, given in equation (8). The IAE weights
the error with time and hence emphasizes the error values over arrange of 0 to T, where T is the expected settling time. |
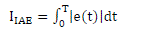 (8) (8) |
| B. Termination criteria |
| Optimization algorithm will automatically terminate execution either when the number of iterations gets over or with
the attainment of acceptable fitness value. Fitness value, in this case is nothing but reciprocal of the error, since we
consider for a minimization of objective function. In this paper the termination criteria is considered to be the
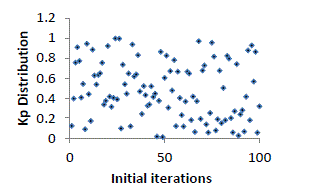
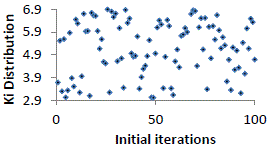
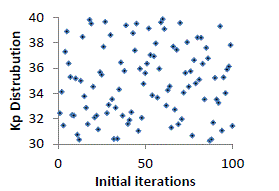
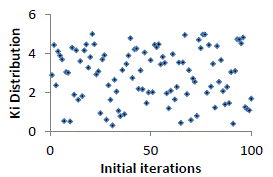
attainment of maximum number of iterations. The variation of the values (Kp,Ki) for four models during first iteration
are sketched and shown in figure2- 9. |
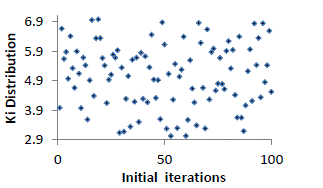
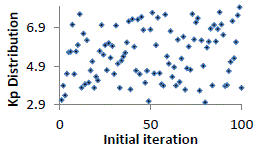
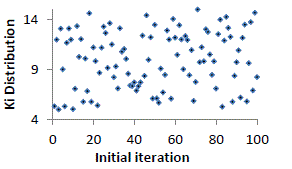
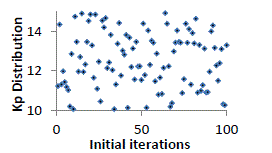
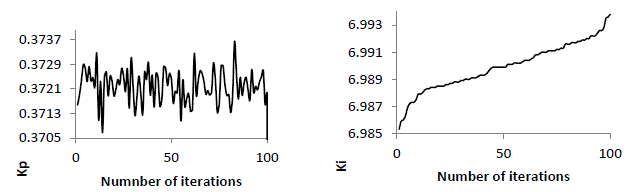
| For each iteration the best among the 100 particles considered as potential solution is chosen. Therefore the best values
for 100 iterations for four models are sketched and shown in figure10-13 with respect to iterations for Kp and Ki. |
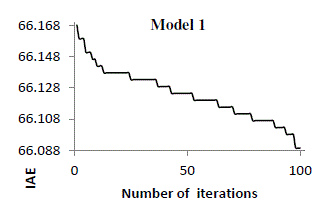
| The PI controller was formed based upon the respective parameters for 100 iterations, and the gbest (global best)
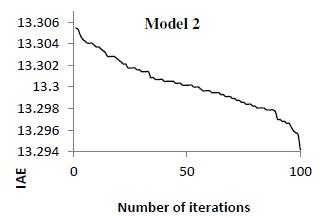
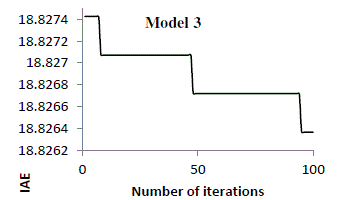
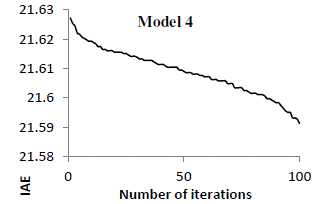
solution was selected for the set of parameters, which had the minimum error. A sketch of the error based on IAE
criterion for 100 iterations is given in figure.14 -17 for four models. |
| It was seen from figure 14-17 that the error value tends to decrease for a larger number of iterations. As such the
algorithm was restricted to 100 iterations beyond which there was only a negligible improvement. Based on PSO
algorithm for the application of the PI tuning, the tuned PI parameters were tabulated in table III. |
VI. RESULT AND DISCUSSION |
| After the tuning process is done through adaptive method and proposed PSO technique, analysis was performed for
step change; with the help of simulation environment application to the conical tank is examined. The time domain
specifications comparison for the obtained models with the designed controller is presented in table IV. Four models
was obtained as 0-1.44cm as model-1, 1.44-5.76cm as model-2, 5.76-12.83cm as model-3 and 12.83-23.04 cm .The
four models are represented as first order transfer function with delay time. |
| The most important feature of the paper is presented in this section. The simulated responses of the conical tank of
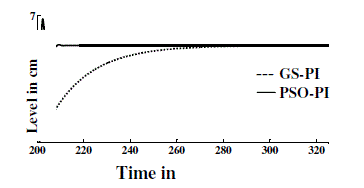
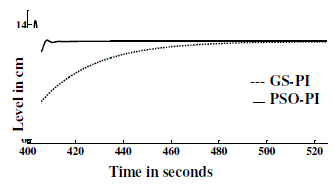
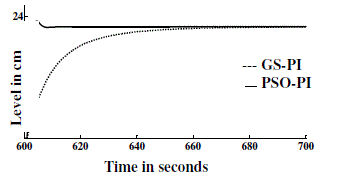
various set points with various PI controller settings are presented in the figures 18-21. The response of the process was
observed by giving set point change at various time instant of 1.4cm, 5.7cm, 12.8cm and 23cm. |
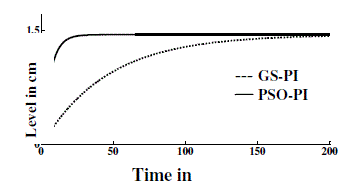
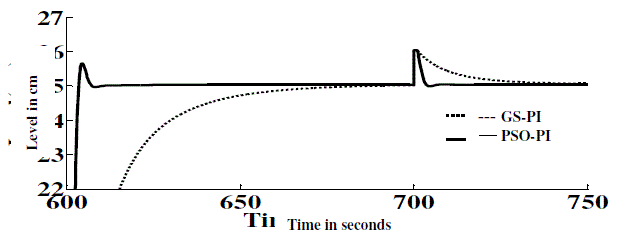
| Figure 22 clearly states that how fast the PSO based PI controller reacts to disturbance compare to GS based PI
controller. A process is disturbed at the time of 700 seconds, the proposed PSO-PI controller reacts faster and process
variable attains steady state in 6 seconds for setpoint 25cm. |
VII. CONCLUSION |
| An analysis has been presented here that the tuned PI values based on PSO algorithm was tested in controlling of level
in the conical tank. It comes out with a conclusion that the rise time(Tr) and settling time(Ts) is reduced drastically for
PSO based tuned PI values compared to GS based tuned PI values. The simulation responses for the models are
validated through time domain analysis and the effectiveness of the PSO based controller in time domain specification
are tabulated in table IV. |
| The obtained results demonstrated that the PSO based PI controller yield good results than gain scheduling method. It
is clearly represented in figure 22, a process is disturbed at time 700 seconds, the proposed PSO-PI controller responds
quickly to disturbance and attains steady state within 6 seconds but GS based controller reaches steady state in 60
seconds at reference value of 25cm. The reaction rate of the proposed controller setting is 10 times faster than the GS
based PI controller setting. |
| PSO presents multiple advantages to a designer by operating with a reduced number of design methods to establish the
type of the controller, giving a possibility of configuring the dynamic behaviour of the control system with ease, starting the design with a reduced amount of information about the controller (type and allowable range of the
parameters), but keeping sight of the behaviour of the control system. So this method of tuning can be applied to any
system irrespective of its order and can be proved to be better than the existing traditional techniques of tuning the
controller. |
Tables at a glance |
 |
 |
 |
 |
| Table 1 |
Table 2 |
Table 3 |
Table 4 |
|
| |
Figures at a glance |
 |
 |
 |
 |
 |
| Figure 1 |
Figure 2 |
Figure 3 |
Figure 4 |
Figure 5 |
 |
 |
 |
 |
 |
| Figure 6 |
Figure 7 |
Figure 8 |
Figure 9 |
Figure 10 |
 |
 |
 |
 |
 |
| Figure 11 |
Figure 12 |
Figure 13 |
Figure 14 |
Figure 15 |
 |
 |
 |
 |
 |
| Figure 16 |
Figure 17 |
Figure 18 |
Figure 19 |
Figure 20 |
 |
 |
| Figure 21 |
Figure 22 |
|
| |
References |
- J. G. Ziegler and N. B. Nichols, âÃâ¬ÃÅOptimum settings for automatic controllers,âÃâ¬Ã Trans. Amer. Soc. Mech. Eng., vol. 64, pp. 759âÃâ¬Ãâ768, 1942.
- G.H Cohen and G.A Coon: Theoretical Consideration of Retarded Control , Trans ASME 75,pp.827/834,1953.
- Astrom, K J.;.Hagglund .T , Automatic tuning of simple regulators with specifications on phase and amplitude margins, Automatica, 20,645- 651, 1984.
- Simon Fabri and VisakanKadirkamanathan, Dynamic structure neural networks for stable adaptive control of nonlinear systems, IEEE Transactions on Neural Networks, Vol. 7, No. 5, 1996.
- Asriel U. Levin and Kumpati S. Narendra, Control of nonlinear dynamical systems using Neural Networks- Part II : observability, identification and control, IEEE Transactions on Neural Networks, Vol. 7, No. 1, 1996.
- Yonghong Tan Xuanju and Dang Achiel Van Cauwenberghe, âÃâ¬ÃÅGeneralised nonlinear PID controller based on neural networksâÃâ¬ÃÂ, IEEE, Information decision and control,1999.
- Thomas Beielstein , K.E. Parsopoulos and Michael N. Vrahatis , âÃâ¬ÃÅTuning PSO Parameters Through Sensitivity Analysis, Technical Report of the Collaborative Research Center 531 Computational Intelligence CI--124/02, University of Dortmund, January 2002.
- S. Skogestad,. âÃâ¬ÃÅSimple analytical rules for model reduction and PID controller tuningâÃâ¬ÃÂ. J. Proc. Cont, Vol 13, pp .291 âÃâ¬Ãâ 309, 2003.
- Y Zheng, Liyan Zhang, JixinQianLonghua Ma âÃâ¬ÃÅRobust PID Controller Design using PSOâÃâ¬Ã International Symposium on Intelligent Control IEEE, October 2003.
- T.BartzâÃâ¬ÃâBeielstein K.E. Parsopoulos and M.N. Vrahatis, âÃâ¬ÃÅAnalysis of Particle Swarm Optimization Using Computational StatisticsâÃâ¬ÃÂ, International conference on numerical analysis and applied mathematics ICNAAM-2004.
- Jun Zhao, Tianpeng Li and JixinQian âÃâ¬ÃÅApplication of Particle Swarm Optimization Algorithm on Robust PID controller TuningâÃâ¬ÃÂ, Springerlink-Verlag Berlin Heidelberg , pp. 948-957, 2005.
- Xu, Z.-C, âÃâ¬ÃÅParameter tuning method of robust PID controller based on particle swarm optimization algorithmâÃâ¬Ã Control and Instruments in Chemical Industry 33 (5), pp. 22-25, 2006.
- S. M. Giri raj Kumar, R. Sivasankar, T. K. Radhakrishnan, V. Dharmalingam and N. Anantharaman, âÃâ¬ÃÅParticle Swarm Optimization Technique Based Design of Pi Controller for a Real-Time Non-Linear ProcessâÃâ¬ÃÂ, Instrumentation Science & Technology, Volume 36, Issue 5, 2008 .
- V.R. Ravi., T. Thyagarajan ,âÃâ¬ÃÅApplication of Adaptive Control Technique to Interacting Non Linear Systems, Electronics Computer Technology (ICECT)âÃâ¬ÃÂ, 2011 3rd International Conference, 386 âÃâ¬Ãâ 392, 2011.
- P.Aravind, M.Valluvan2, S.Ranganathan,âÃâ¬ÃÂModelling and Simulation of Non linear TankâÃâ¬ÃÂ, International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering, Vol. 2, Issue 2, February 2013.
- P Aravind, M Valluvan , M Saranya ,âÃâ¬Ã Simulation based Modeling and Implementation of Adaptive Control Technique for Non Linear Process Tank, International Journal of Computer Applications (0975 âÃâ¬Ãâ 8887) Volume 68âÃâ¬Ãâ No.16, 2013.
- D. Mercy, S.M.Girirajkumar, âÃâ¬ÃÅTuning of Controllers for Non Linear Process using Intelligent TechniquesâÃâ¬ÃÂ, International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering, Vol. 2, Issue 9, September 2013.
|