Keywords
|
| Genetic Algorithms, Signal Processing, decimation, digital filter, optimization, resampling. |
I.INTRODUCTION
|
| In signal processing theory there are numerous applications where it is advantageous or even necessary to convert (increase or decrease) the sampling rate [1]. The process of decreasing of an original signal sampling rate to a lower sampling rate by some integer factor is a combination of low pass filtering and decimation process. Sample rate conversion (SRC) often requires less multiplies and add per second when implemented in multiple stages. Even though multistage implementation increases the computation rate of some filter coefficients, the overall multiplies and add per second (MADS) and required coefficient storage are reduced. Moreover, multistage implementation relieves word length requirements of both signals and filter coefficients, which further reduces the computation effort. [1] One another benefit of multistage SRC is usage of special filter structures. For example, half band filters are efficient in decimation by two because one of their polyphase branches is a pure delay [1]. Cascaded integrator-comb decimators [2] [23]are efficient due to their simple, multiplier free structure performs well in narrow stop bands applications. This is x benefits of both of exploited in multistage decimation. Earlier Crochiere and Rabiner quantitatively considered the computational cost of performing sampling rate reduction [1]. Occasional examples of multistage decimation filters appear in more recent literature [3], [4]. For instance, Kale et al. [4] used a cascade of seven stages with a sample-rate reduction of two at each stage. That work employed all-pass infinite impulse response recursive digital filters and was concerned with efficient hardware realizations. However, the best way to split mentioned operations into its component stages is not known to best of our knowledge [11]. A possible solution for the design of multistage decimators using finite impulse response (FIR) filters based upon the minimization of the multiplies and add per sec is presented in [20] and [21]. Starting from the method for determination of multistage decimation ratios published in [20], the method for design of the optimized multistage decimation filter chain for two and three-stages and four stage is analysed and number of stages are finally decided for the case which have minimum multiplies and addition per second as three [1]. The aim is to minimize overall multiplication and addition per second which can be achieved by reducing overall number of multipliers, and by shifting the most of multipliers to the lower sampling rate [22]. In this work genetic algorithm is used for finding optimum decimation factor of multistage decimator components for minimum multiplication and addition per second. Genetic algorithm is an optimization technique based on natural evolution that is the change over a long period of time .The Genetic Algorithms [7], [9] provide robust and efficient search in complex spaces. Survival of the fittest “genes” and structured yet randomized genetic operations are the basic philosophies behind the algorithms. The main advantages of Genetic Algorithms have been successfully applied to control problems in ATM networks, such as bandwidth allocation [16] and buffer management [17]. Recently, they have been applied to point-to-point routing [18] and spanning tree problem [19] in communication networks. |
| The results of the proposed GA-based method is compared with the previous methods. The simulation results show that the proposed method is also able to find the almost same solution of multistage decimator optimisation problem decreasing mathematical complexity even for higher decimation ratio. In the section 2 , the multistage decimator structure is discussed. In Section 3, genetic algorithm is discussed .In section 4 solution for multistage optimization problem is proposed using GA. Design examples are given in Section 4, and conclusions are drawn in Section 5. |
II. OPTIMIZED MULTISTAGE DECIMATION
|
| Multiple stages for decimation (or interpolation) can reduce the number of filter coefficients in the filter specifications. Discussion [1] shows that transition width, filter length of filter stage depends on the decimation rate of that particular stage. So determination of optimal decimation rate per stage is very important in multistage decimation. If the overall sampling rate decimation ratio D can be factored into the product |
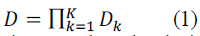 |
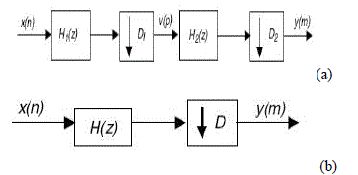
| where ïÿýïÿýïÿýïÿý is an integer, then the decimators can be implemen ted using K stages as it is shown in Fig. 1(a), where x(n) and y(m) denote discrete input and discrete output signal and H(z) is the transfer function. For the design and analysis purposes, diagram shown in Fig. 1(a) can be redrawn into the equivalent single-stage form given in Fig. 1(b) [1], [2] where D=D1*D2. and H(z)= H1(z)*H2(z) |
| Let Δf=(fc-fp)/fs denotes the normalized transition bandwidth, where fc stands for the stop band edge frequency, fp stands for the pass band edge frequency, and fs denotes sampling frequency. In order to minimize total number of multiplications and additions per second approximate objective function [1] is used given in equation (2) |
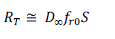 (2) (2) |
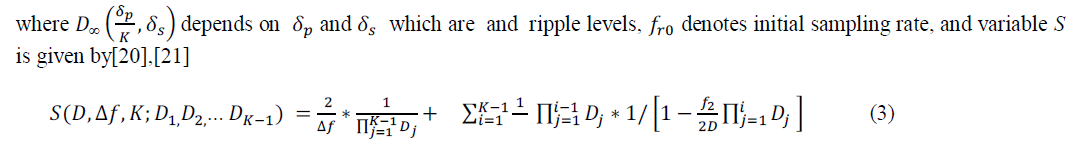 |
| where .It is obvious that to obtain minimal value of function RT the multivariate function S has to be minimized, for a given number of stages, K. As multivariate function S is dependent on decimation factor of component stages and it can be only minimized using optimum values of D. So the above function is optimised for the case K=2 and K=3 i.e. three stage and two stage decimator .Corresponding values of individual decimation ratio and minimum value of objective function is calculated using proposed method which provides a logical comparison for choosing number of stages in decimator. |
III. (1) THE PROPOSED GENETIC ALGORITHM APPROACH
|
| III.1.1 Genetic Algorithm |
| The basic principles of GA were first proposed by Holland [7]. Thereafter, a series of literature [8], [9] and reports [10], [11], [12] became available. GA is an optimization technique inspired by the mechanism of natural selection, a biological process the individuals with the considered best characteristics to adapt to the environment are more likely to reproduce and survive. These advantageous individuals mate between them, producing descendants similarly characterized, so favourable characteristics are preserved and unfavourable ones destroyed, leading to a progressive evolution of the species. |
| Artificial genetic algorithm aims to improve the solution to a problem by keeping the best combination of input variables. It starts with the definition of the problem to optimize , generating an objective function to evaluate the possible candidate solutions (chromosomes).An initial random population of n individuals is generated. The population size, which is usually a user-specified parameter, is one of the important factors affecting the scalability and performance of genetic algorithms. For example, small population sizes might lead to premature convergence and yield substandard solutions. On the other hand, large population sizes lead to unnecessary expenditure of valuable computational time. The size of this population varies from one problem to another although, some guidelines are given in [15]. These n individuals are called chromosomes that are symbolized by binary strings, where each binary position of the chromosome is called a gene and denotes a specific characteristic (input variable). |
| Each chromosome is evaluated in the objective function and the best individuals are selected to survive for mating (parents), while the worse ones are discarded to make room for new descendants. The next step is to create a second generation of individuals, based on the information of the parents. There are several ways of mating [14]. |
| The parent’s binary information to the child is transferred using genetic operators crossover point and mutation. New parents are randomly selected for each new child and the process continues until the chromosome population grows back to the original size n. The purpose of mutation is to introduce diversity into the population, allowing the algorithm to avoid local minima by generating new gene combinations in the chromosomes. |
| Finally, after mutation is done the new generation of chromosomes is evaluated with the objective function and used in the next iteration of the described algorithm. The algorithm iterates until a maximum number of chromosome generations are created or a satisfactory solution is reached |
| III.1.2 The Proposed Approach Optimum Decimation ratio of multistage Decimator is calculated so that multiplies and adds per sec can be minimised. When K=2 (two stage decimator ) the objective function given in[20] for minimum computation load will become as |
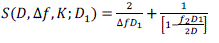 (3) (3) |
| when K=3(three stage decimator) the objective function given in[20] for minimum computation load will become as |
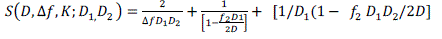 (4) (4) |
| Where .Now GA act as heuristic search method and is used for an efficient searching and fast converging tool for the optimum decimation factor detection in the above problem. For a clearly defined above problem the simple GA works with following parameter setting as follows: |
| 1. Population: Initial Population type specifies the type of the input to the fitness function. The population used here is of Double vector type. The population size which defines number of individuals in a generation is taken here as 20. An initial population is created that satisfies the bounds .The bound on the decimation factor of first stage is based on iterative method chosen by [5]. Similarly the decimation factor of subsequent stages will considered to be near 2 as it is the minimum integer decimation factor. The initial range for the population is also given by the help of these bounds . 2. Fitness function: Fitness function in the present case is equation no.(3) for each individual in the population. The main purpose of fitness function is to get best individual for optimum detection. Now the scaling function converts raw fitness scores returned by the fitness function to values in a range that is suitable for the selection function. Scaling function Rank is used here which scales the raw scores based on the rank of each individual, rather than its score. The rank of an individual is its position in the sorted scores. The rank of the fittest individual is 1, the next fittest is 2, and so on. Rank fitness scaling removes the effect of the spread of the raw scores. |
| 3. Selection: The selection function chooses parents for the next generation based on their scaled values from the fitness scaling function. Stochastic uniform lays out a line in which each parent corresponds to a section of the line of length proportional to its expectation. The algorithm moves along the line in steps of equal size, one step for each parent. At each step, the algorithm allocates a parent from the section it lands on. The first step is a uniform random number less than the step size. |
| 4. Reproduction: It determine how the genetic algorithm creates children at each new generation. Elite count specifies the number of individuals that are guaranteed to survive to the next generation which is set as 2 in this case .The Elite count must be a positive integer less than or equal to Population size. Now Crossover and Mutation are performed. The fraction of the next generation that crossover produces is taken as 0.8. Mutation produces the remaining individuals in the next generation. So for the initial population of 20 , elite count of 2 , and the crossover fraction 0.8 ,there are 18 individuals other than elite children, so the algorithm rounds 0.8*18 = 14.4 to 14 to get the number of crossover children. The remaining four individuals, other than elite children, are mutation children. |
| 5. Now fitness function is calculated again for these new children and process is repeated until the stopping criteria is met. The algorithm runs until the weighted average change in the fitness function value over generations is less than 10- 6 . Each iteration of this process is called a generation. A GA is typically iterated for anywhere from 50 to 500 or more generations. The entire set of generations is called a run. At the end of a run there are often one or more highly fit chromosomes in the population. Since randomness plays a large role in each run, two runs with different randomnumber seeds will generally produce different detailed behaviours. GA researchers often report statistics (such as the best fitness found in a run and the generation at which the individual with that best fitness was discovered) averaged over many different runs of the GA on the same problem. |
IV. RESULT AND DISCUSSION
|
| This section presents some results obtained by applying the optimization approach. For given specification in [5] the decimation factor of multistage component is calculated using GA. |
 |
| The results of the optimization problem considering different number of stages are shown in Table I. |
| Above table shows that minimum computation is required for K=3 for same set of specifications. Now the results of proposed approach for K=3 are compared with set of eligible decimation factors chosen by the previous two approaches . A suitable initial estimate for D1 for iterative method is chosen by [5] so that the bounds on initial population of decimation factor of first stage can be set. One more assumption is that the minimum decimation factor of further stages must be bound near 2 as having decimation factor 1 converts the problem in less stage decimation .The result of generation with best fitness is averaged and the numerical value of the individual matches with the results in [20]. |
| As GA gives different result in each run due to randomness results for 100 runs are then averaged. These decimation ratios have been given in decimal form in order to allow direct comparison with [1]. In practice, the ratios must take integer values and for the above case the values may be D1= 6, D2= 2, D3=2 . Specifically, this implies that the overall decimation rate should be chosen to be highly composite (nonprime) for high rates. These points are discussed in more detail where some guidelines for delivering integer-valued rates are presented [5]. |
| In addition decimation rates D1 , D2 , and D3 = D/D1D2 are plotted on a log–log scale for K = 3 stages using the results of proposed approach for Δf =0.5 and Δf= 0.1 in Fig.3. |
 |
V. CONCLUSION
|
| In this paper, novel signal processing technique is proposed using genetic algorithm for optimization of individual decimation ratio of multirate multistage decimators by minimizing multiplication and addition per second of the filter . For the class of multistage decimators considered in [1], independent decimation ratios are calculated and compared . The proposed multistage decimator design method uses genetic algorithm technique for any specification set even of higher decimation ratio in a successful way. |
Tables at a glance
|
 |
 |
| Table 1 |
Table 2 |
|
| |
Figures at a glance
|
 |
 |
| Figure 1 |
Figure 3 |
|
| |
References
|
- Crochiere R. E. and Rabiner, L. R. 1975.“Optimum FIR digital filter implementations for decimation, interpolation, and narrowband filtering,”IEEE Trans. Acoust., Speech Signal Processing, vol. ASSP-23, 444.
- Cliffs Englewood Multirate Digital Signal Processing., NJ:Prentice-Hall, 1983.
- Krukowski A., Kale I, Hein K., and. Cain G. D,1994 “A design technique for polyphase decimators,” in Proc. 2nd Int. Symp. on DSP for Communications Systems( Apr 1994). 26–29.
- Kale I., Morling R. C. S., Krukowski A., and Tsang C.-W 1995.“A highfidelity decimator chip for the measurement of sigma-delta modulator performance,” IEEE Trans. Instrum. Meas., vol. 44 (Oct.1995), 933–939.
- Feinleib R. E. and 2001 “Analysis, design, and implementation of a digital multistage subband tuner,” TRW Syst. Information. Technol. Rev. J.,23, Spring/Summer 2001.
- Shively R. R 1975 “On multi-stage FIR filters with decimation,” IEEE Trans.Acoust., Speech, Signal Processing, vol. ASSP-23, 1975.
- Holland J. H 1975. Adaption in Natural and Artificial Systems. Cambridge, MA: MIT Press.
- Van Nostrand Reinhold. 1991 Handbook of Genetic Algorithms. New York.
- Goldberg D. E 1995 Genetic Algorithms in Search, Optimization, and Machine Learning.
- Beasley D., Bull D. R. , and. Martin R. R 1993 “An overview of genetic algorithms: Part I-Fundamentals,” Univ. Comput., vol. 15, no. 2, 58-69.
- D Beasley D., Bull D. R. , and. Martin R. R 1993, “An overview of genetic algorithms: Part 2-Research topics,”Univ. Comput., vol. 15, no.4, pp. 170-181.
- Srinivas M. , and Patnaik L. M 1994. “Genetic algorithms: A survey,” Computer(june 1994) 17-26.
- Whitley D. 1993 “A genetic algorithm tutorial,” Dept. Comput. Sci, Colorado State Univ., Tech. Rep. CS-93 103,
- Haupt, Randy. Haupt, Sue 2004. Practical Genetic Algorithms. Second edition. New Jersey: John Wiley & Sons
- Mahfoud S. W.,1994 “Population sizing for sharing methods,” Dept. Comput. Sci.,Univ. Illinois at Urbana-Champaign, IlliGAL Rep. 94005
- Pan H. and Wang I. Y 1991.“The bandwidth allocation of ATM through genetic algorithm,”IEEE GLOBECOM ‘91, 125-129.
- . Chou L.-D. and. Wu J.L.C. 1995. “Buffer management using genetic algorithms and neural networks,” IEEE GLOBECOM ’95, 1333-1337.
- Shimamoto N., Hiramatu A., and Yamasaki K. 1993. “A dynamic routing control based on a genetic algorithm,” 1993 IEEE International Conference on Neural Network,1123-1128.
- Palmer C. C. and Kershenbaum A 1993. Two algorithms for finding optimal communication spanning trees.Technical Report, IBM T. J. Watson Research Center, Yorktown Heights, NY.
- Coffey M.W. 2003 “Optimizing multistage decimation and interpolation processing,” IEEE Signal Process. Lett., Vol. 10,No. 4, pp. 107-110, Apr. 2003.
- Coffey M.W. 2007 “Optimizing multistage decimation and interpolation processing – part II,” IEEE Signal Process. Lett., Vol. 14, No. 1, 24-26, Jan. 2007.
- DE Troncoso Romero, M Laddomada” Optimal Sharpening of Compensated Comb Decimation Filters: Analysis and Design “The ScientificWorldJournal Volume 2014.
- Guillermo A. Jaquenod, Javier Valls, Javier Siman”Efficient FPGA Hardware Reuse in a Multiplierless Decimation Chain” International Journal of Reconfigurable ComputingArticle ID 546264, Volume 2014 .
|