Research and Reviews - International Journals

International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Menu

ISSN ONLINE(2278-8875) PRINT (2320-3765)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

PAPR Reduction in MU- MIMO-OFDM Using FITRA with L1 Minimization

M.Suneetha1, Ritesh2, N.Pushpalatha3
  1. M.Tech (DECS) Student, Department of ECE, Annamacharya Institute of Technology and Sciences, Tirupati, India
  2. Assistant Professor, Department of ECE, Annamacharya Institute of Technology and Sciences, Tirupati, India
  3. Assistant Professor, Department of ECE, Annamacharya Institute of Technology and Sciences, Tirupati, India
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Abstract

In this paper PAPR is reduced at downlink scheme by using PMP pre coding at transmitter section. By using FITRA algorithm with l infinity minimization we can reduce PAR, but practical implementation is complex, to overcome this we use l1 minimization in addition to FITRA algorithm which can reduce computational complexity of FITRA. We compare our results with FITRA.We prove that our method will reduce computational complexity of FITRA.

 

INTRODUCTION
After more than thirty years of research and growth carried out in the field of communication OFDM has been widely implemented in high speed digital communication. OFDM has its major benefits of higher data rates and better performance. The higher data rates are achieved by use of multiple carriers and performance improved by use of guard interval which leads to removal of Inter Symbol Interference (ISI) . OFDM has several features which makes it more advantageous for high speed data transmission. These features include High Spectral competence, Robustness to Channel Fading, and Immunity to Impulse Interference, litheness and Easy Equalization. In spite of these benefits there are some drawbacks such as PAPR, Offset frequency and Inter Carrier Interference (ICI) between sub-carriers. Practical wireless channels typically exhibit frequency selective fading and a low-PAR precoding solution suitable for such channels would be desirable. rather, the solution should be such that the complexity required in each (mobile) terminal is small (due to stringent area and authority constraints), whereas heavier dispensation could be afforded at the BS. Orthogonal frequency-division multiplexing (OFDM) is an efficient and well-established way of commerce with frequency selective channels. In addition to simplify the equalization at the receiver, OFDM also facilitates per-tone influence and bit allocation, scheduling in the frequency domain, and band shaping. However, OFDM is known to suffer from a high PAR [9], which necessitate the use of linear RF components (e.g., power amplifiers) to avoid out-ofband radiation and signal distortions. Unfortunately, linear RF components are, in general, more costly and less power efficient than their non-linear counterparts, which would eventually result in exorbitant costs for large-scale BS implementations having hundreds of antennas. Therefore, it is of paramount consequence to reduce the PAR of OFDMbased large-scale MU-MIMO s to facilitate parallel low-cost and low-power BS implementations.

A. Contributions
In this paper, we develop a novel system broadcast scheme for large-scale MU-MIMO-OFDM wireless s, which only affects the signal processing at the BS while leaving the meting out required at each terminal undamaged. The key idea of the proposed scheme is to exploit the excess of degrees-of-freedom (DoF) offered by equip the BS with a large number of antennas and to jointly perform MU precoding, OFDM modulation, and PAR reduction, referred to as PMP in the remnants of the paper. Our contributions can be summarized as follows: • We formulate PMP as a convex optimization problem, which in cooperation performs MU precoding, OFDM modulation, and PAR reduction at the BS. • We develop and examine a novel optimization algorithm, referred to as fast iterative truncation algorithm (FITRA), which is able to find the solution to PMP efficiently for the (typically large) dimensions arising in large-scale MU-MIMO-OFDM s. • We present numerical simulation results to demonstrate the capability of the proposed MUMIMO- OFDM system spread scheme. Specifically, we analyze the trade-offs between PAR, error-rate performance, and out-of-band radiation, and we present a comparison with conventional preceding schemes. b. Notation lowercase bold-face writing for column vectors and upper-case bold-face letters designate matrix. The M×M distinctiveness matrix is denoted by Im. The M×N all zeros matrixes by 0m×n. and Fm refers to the M×M discrete Fourier transform(DFT) matrix.

B. Outline of the Paper
The remainder of the paper is organized as introduces the model and summarizes important PAR-reduction concepts. The proposed system transmission scheme is detailed and the fast iterative truncation algorithm (FITRA) is developed.

EXISTING METHOD

I). FITRA ALGORITHM
Compressed Sensing is the name assigned to the idea of encoding a large sparse signal using a relatively small number of linear measurements, and minimizing the `1-norm (or its variants)in order to decode the signal. New results reported by Candes et al [4, 2, 3], Donoho et al [12,53, 13] and others [45, 51] stimulated the current burst of research in this area. Applications of compressed sensing include compressive imaging [56, 57, 47], medical imaging, multisensory and distributed compressed sensing [1], analog-to-information conversion [52, 27, 30, 29], and missing data recovery. Compressed sensing is attractive for these and other potential applications because it reduces the number of measurements required obtaining a given amount of information. The trade-off is the addition of a non-trivial decoding process.
CS channel estimation method concerns the sparse reconstruction problem of estimating an unknown sparse channel vector from an observed vector of measurements R∈CM based on the linear model, namely the measurement
by omitting the superscript for brevity.
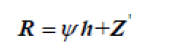image
where = m N m ψ φ F ∈C × is a known measurement matrix, Z' is the measurement noise vector, and channel vector h is L sparse,
where L is the number of multipath and is much
where = m
m ψ φ F ∈C × is a known measurement matrix, Z' is the measurement noise vector, and channel vector h is L sparse, where L is the number of multipath and is much
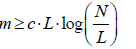image
where c > 0 is a constant. Secondly, the measurement matrix ψ should satisfy the RIP, namely, for all Lsparse vector h, we have
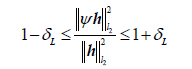image
Where 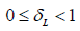image is the isometry constant,
image

A. PAPR Problem
One of the new problems emerging in OFDM s is the so-called Peak to Average Power Ratio (PAPR) problem. The input symbol stream of the IFFT should possess a uniform power spectrum, but the output of the IFFT may result in a non-uniform or spiky power spectrum. Most of transmission energy would be allocated for a few instead of the majority subcarriers. This problem can be quantified as the PAPR measure. It causes many problems in the OFDM at the transmitting end.

B. Effect of PAPR
There are some obstacles in using OFDM in transmission in contrast to its advantages [3]:
(i) A major obstacle is that the OFDM signal exhibits a very high Peak to Average Power Ratio (PAPR).
(ii) Therefore, RF power amplifier should be operated in a very large linear region. Otherwise, the signal peaks get into non-linear region of the power amplifier causing signal distortion. This signal deformation introduces intermediation among the subcarriers and out of band radiation. Thus, the power amplifiers should be operated with large power back offs. On the other hand, this leads to very inefficient amplification and expensive transmitters. Thus, it is highly desirable to reduce the PAPR.
(iii) These large peaks cause saturation in power amplifiers, leading to inter modulation products among the subcarriers and disturbing out of band energy. Therefore, it is desirable to reduce the PAPR.
(iv) To reduce the PAPR, several techniques have been proposed such as clipping, coding, peak windowing, Tone Reservation and Tone Injection. But, most of these methods are unable to achieve simultaneously a large reduction in PAPR with low complexity, with low coding overhead, without performance degradation and without transmitter receiver symbol handshake. (v) Complexity is increased in the analog to digital and digital to analog converter.

C. Calculation of PAPR:
The peak to average power ratio for a signal x(t) is defined as
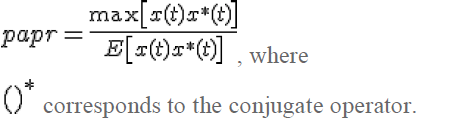image
Expressing in decibels
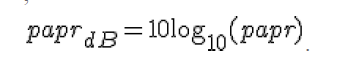image

PROPOSED TECHNIQUES

Sparse representation:
Norm minimization Problems:
• L1 norm: ||x||=
Minimize ||Ax-b|| is equivalent to this LP in x R^n, s R^n:
Minimize t
Subject to Ax-b≤s
Ax-b≥-s
• L∞ norm: ||x||∞=max i{|Xi|}
Minimize ||Ax-b||∞ is equivalent to this LP in x R^n, t R:
minimize t
subject to Ax-b≤t1
Ax-b≤-t1

Dual Linear Programming
• Primal Problem in standard form:
Minimize cTx
Subject Ax=b
x≥0
• Write down Lagrangain using Lagrange multipliers lamba,v:
L(x,lamda,v)=cTx-+vT(Ax-b)=-bTv+(c+A┬v-lamda)Tx
• Find Lagrange dual function:
g(lamda,v)=inf L(z,lamda,v)=-bTv+inf{(c+aTv-lamda)T.x}
since a linear function is bounded below only if is identically Zero,we
have
g(lamda,v)=
l1-minimization (`1-min) has been one of the hot topics in the signal processing and optimization communities in the last five years or so. In compressive sensing (CS) theory [9], [16], [8], it has been shown to be an efficient approach to recover the sparsest solutions to certain underdetermined systems of linear equations. More specifically, assuming there exists an unknown signal x0 2 Rn, a measurement vector b 2 Rd can be generated by a linear projection b = Ax. If we assume the sensing matrix A to be full-rank and overcomplete, i.e., d < n, an `1-min program solves the following convex optimization problem
(P1) : min kxk1 subject to b = Ax: (1)
The formulation of (P1) constitutes a linear inverse problem, as the number of measurements in b is smaller than the This work was partially supported by.The views and conclusions contained in this document are those of the authors and should not be interpreted as representing the official policies, either expressed or implied, of the Army Research Laboratory or the U.S. Government. The U.S. Government is authorized to reproduce and distribute for Government purposes notwithstanding any copyright notation hereon. A. Yang and S. Sastry are with the Department of Electrical Engineering and Computer Sciences, University of California, Berkeley, USA. A. Ganesh, and Y. Ma are with the Coordinated Science Laboratory, University of Illinois, Urbana, USA. Y. Ma is also with the Visual Computing Group, Microsoft Research Asia, Beijing, China. Corresponding author: Allen Yang, Cory Hall, University of California, Berkeley, CA 94720. Email:yang@eecs.berkeley.edu. Tel: 1-510-643-5798. Fax: 1-510-643-2356. number of unknowns in x. However, CS theory shows that if x0 is sufficiently sparse and the sensing matrix A is incoherent with the basis under which x0 is sparse (i.e., the identity matrix in its standard form (1)), x0 can be exactly recovered. This sparsity-seeking property of (P1) has been shown to have tremendous applications in geophysics, data compression, image processing, sensor networks, and most recently computer vision. The reader is referred to [9], [2], [8] for a comprehensive review of these applications. Traditionally, (P1) has been formulated as a linear programming (LP) problem, such as in basis pursuit (BP) [11]. However, one can show that the computational complexity of these general-purpose algorithms is often too high for many real-world, large-scale applications. Alternatively, heuristic greedy algorithms have been developed to approximate (P1), which are also significantly faster than using LP. Orthogonal matching pursuit (OMP) [14] and least angle regression (LARS) [18] are two well-known algorithms in this category. Empirically, these greedy algorithms often can find sufficiently good solutions to approximate (P1). However, they may also fail in some conditions (one negative example for OMP is discussed in [38]). In practice, the exact

`1-MINIMIZATION ALGORITHM
A. Gradient Projection Methods
We first discuss gradient projection (GP) methods that seek sparse representation x along certain gradient direction, which induces much faster convergence speed. The approach reformulates the `1-min as a quadratic programming (QP) problem compared to the LP implementation in PDIPA.We start with the `1-min problem (P1;2). It is equivalent to the so-called LASSO objective function
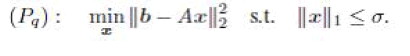image

B. Homotopy Methods
Both PDIPA and GP require the solution sequence to be close to a “central path”, which is often difficult to satisfy and computationally expensive in practice. A natural question arises: Are there any fast algorithms that are suitable for largescale applications and yet can recover the sparsest solutions in similar conditions as `1-min? In this section, we overview one such approach called homotopy methods [37], [31], [17]. The algorithm has intimate connection with two other greedy `1-min approximations, namely, least angle regression (LARS) [18] and polytope faces pursuit (PFP) [38]. For instance, if a k-sparse signal is sufficiently sparse, all three algorithms can find it in k iterations. On the other hand, LARS would never remove indices from the current sparse support set, while the general homotopy and PFP include mechanisms to remove coefficients from the sparse support during the iteration. More importantly, the homotopy algorithm provably solves `1-min (P1), while LARS and PFP are only approximate solutions.

C. Iterative Shrinkage-Thresholding Methods
The homotopy algorithm employs a more efficient iterative update rule that only involves operations on those submatrices of A corresponding to the nonzero support of the current vector x. However, it may lose its computational competitiveness when the sparsity of x grows proportionally with the observation dimension d. In such scenarios, the complexity may still approach the worst-case upper-bound O(n3). In this section, we discuss iterative shrinkage-thresholding (IST) methods

EXPERIMENTAL RESULTS

CONCLUSION
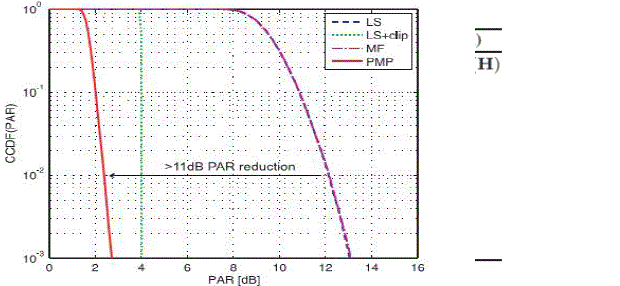
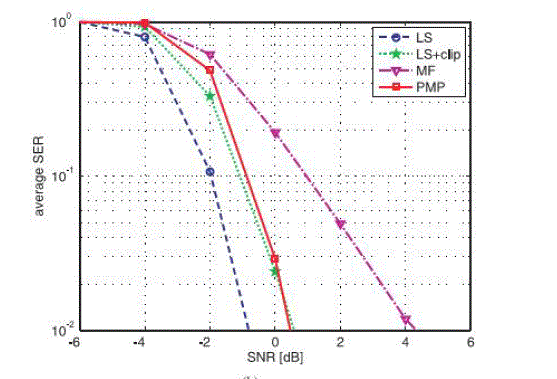
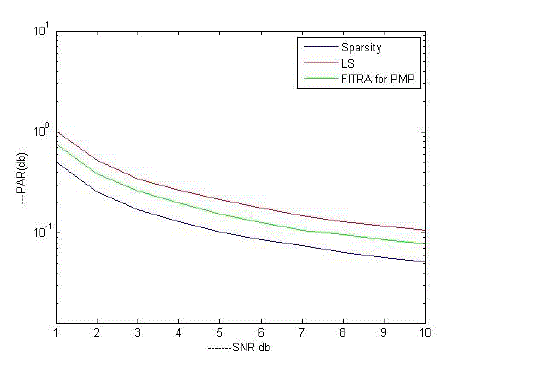
In this paper, we apply sparse representation based on l1 minimization applied to FITRA algorithm which is proposed in state-of –art methodology [1], by using sparse representation, we can reduce PAR values drastically.We compare our results with state-of-art criteria like FITRA using l-infinity minization,and we prove that our methodology will give better results based on PAR values which we obtained. It is applicable to hardware implementation also.

FUTURE WORK
Here by applying Mu (μ)-Law compression and expansion at the transmitter and receiver, is simple and nonlinear method for reducing PAPR.It is having less computational complexity and can achieve better results.

Figures at a glance
Figure Figure Figure Figure Figure
Figure 1 Figure 2 Figure 3 Figure 4 Figure 5

References