Keywords
|
| Low-Density-Parity Check (LDPC), Orthogonal Frequency Division multiplexing (OFDM), Space time block codes (STBC), Peak-to-Average Power Ratio (PAPR). |
INTRODUCTION
|
| OFDM system has been used for high speed digital communications such as Digital Audio Broadcasting, Digital Video Broadcasting, digital High-Definition Television and ADSL (Asymmetric Digital Subscriber Line) due to robustness to the narrowband interference and severe multi-path fading. |
| However, some drawbacks are still unresolved in the OFDM systems. One of the major problems is high Peak-to- Average Power Ratio. This high PAPR forces the transmit power amplifier to have a large back-off in order to ensure linear amplification of the signal, which significantly reduces efficiency of the amplifier. |
| Recently, researchers have proposed various approaches to reduce the PAPR including companding [1],clipping, nonlinear companding transforms [2,3], selected mapping (SLM) [4], Hadamard transforms [5] and DCT [6]. A large PAPR corresponds to a high probability of the OFDM signal being clipped when passing through a power amplifier at the end of the transmitter. Clipping reduces the signal power but degrading bit error rate (BER) performance and causing non- linear phenomena such as spectral spreading. Spectral spread causes degradation of spectral efficiency. |
| In this paper we studied the performance of the OFDM system by using linear coding techniques such as Low Density Parity Check(LDPC) codes and convolutional coding. In this respect we present a design of a simple LDPC encoder to work in conjunction with new coding-based PAPR reduction technique for better system performance. Moreover, this LDPC design has been compared to the Quasi-cyclic LDPC encoder andthe convolutional coding scheme. The reviewed work has been compared with some PAPR reduction techniques such as selective mapping (SLM)and Partial Transmit Sequence (PTS).Some methods are designed based on employing redundancy, such as coding [7], [8], selective mapping with explicit or implicit side information [9], [10] , or tone reservation [11], [12]. An apparent effect of using redundancy for PAPR reduction is the reduced transmission rate. PAPR reduction may also be achieved by using extended signal constellation, such as tone injection [11], or multi-amplitude CPM. The associated drawback is the increased power and implementation complexity. A simple PAPR reduction method can be achieved by clipping the time-domain OFDM signal. |
| OFDM has several significant advantage over traditional serial communication, such as ability to support high data rates for wide area coverage, robustness to multipath fading and a greater simplification of channel equalization. Because of these advantages, OFDM has been adopted in both wired and wireless application in recent years (Reimers 1998; Nee and Prasad 2000; Saltzberg 1998; Juntti et. al. 2005) including wireless networking (IEEE 802.11). The main drawback of OFDM is its high PAPR which distorts the signal if the transmitter contains nonlinear components such as power amplifier and causes some deficiencies such as spectral spreading,inter-modulation, and changing in signal constellation (Nee and Prasad 2000; Wu and Zou 1995). Therefore, average signal power must be kept low in order to prevent the transmitter amplifier and other circuitry limiting. Minimizing the PAPR allows a higher average power to be transmitted for a fixed peak power, improving overall signal to noise ratio at the receiver. There are many solutions in the literature to reduce the effect of PAPR in the OFDM signals, such as Golay sequences, Cyclic coding,clipping and filtering,Selective mapping; and multiple signal representation techniques (Wunder 2004; Han and Lee 2005; Tarokh and Jafarkhani 2000; Tellado 1999; Krongold and Jones 2003; Jiang and Zhu 2004). |
| The paper is organized as follows. In section II, some basics about PAPR problem in OFDM is given. Section III describes PAPR reduction techniques. Conclusions are given in section IV. |
PAPR IN OFDM SYSTEM
|
| Orthogonal Frequency Division Multiplexing (OFDM) has been widely adopted for high data rate transmission purposes due to its superior performance such as robustness to frequency selective fading channel and high spectral efficiency. Its success is due to various factors particularly, multiple orthogonal carriers, however, as the output is the superposition of multiple carriers which increases instantaneous power outputs greatly i.e. far higher than the mean output power when the phase of these carriers are same, is popularly known as Peak-to-Average- Power Ratio |
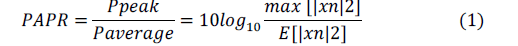 |
 |
PAPR REDUCTION TECHNIQUES
|
| LDPC codes have recently received much attention from the communications industry because of their excellent errorcorrecting performance as well as having a highly parallelizable decoding algorithm even though they were developed half century ago. In 2003, the LDPC code beat six alternative turbo codes to become the error correcting code in the second generation standard for satellite transmission of digital television and has already been proposed for the next generation digital terrestrial television standards. |
| In designing the LDPC code the following design properties should be observed in order to obtain good code performance; first the code should be long enough, as performance improves with the code length. Second, few small cycles in the code bipartitegraph since too many of them will seriously degrade the error-correcting performance. Finally, using carefully designed LDPC codes with irregular node degree distributions proved to remarkably outperform regular ones. It has been well recognized that the conventional method for encoder/decoder design (first construct a code exclusively optimized for error-correcting performance, and then implement the encoder and decoder for that code) is not applicable to LDPC coding system implementations. Consequently, joint coding design has become the key in most recent work (Mansour and Shanbhag 2003; Mansour and Shanbhag2003 ;ChenandHocevar 2003; Zhang and Parhi 2004; Nikolic and Anantharam 2002). However, two challenges still remain unresolved: (1) Complexity reduction and effective VLSI architecture design for LDPC encoder remain largely unexplored; (2) Given the desired node degree distribution, no systematic method has ever been proposed to construct the code for hardware implementation. In this paper, an LDPC code design is proposed to help in simplifying the hardware design. From the work by Urbanke and Richardson (Richardson and Urbanke 2001), it can be seen that the encoding complexity could be reduced significantly by using a criteria based on back-substitution once the parity check matrix has been changed into an upper matrix. On the other hand, despite the parity check matrix is approximate upper matrix the back-substitution operation is highly reused. This drawback mitigated in (Zhang and Parhi 2004) (where the back substitution operation is replaced by a few matrix-vector multiplications. |
| LDPC CODING TECHNIQUE FOR MIMO-OFDM SYSTEM PERFORMANCE IMPROVEMENT |
| LDPC encoder is used for reducing the PAPR problem in OFDM. This proposed linear coding technique using LDPC encoder for PAPR reduction is better than the previous PAPR reduction techniques such as Clipping with Filtering Companding and moreover the performance of LDPC codes in OFDM symbol spreading is better than BCH and Turbo coding. |
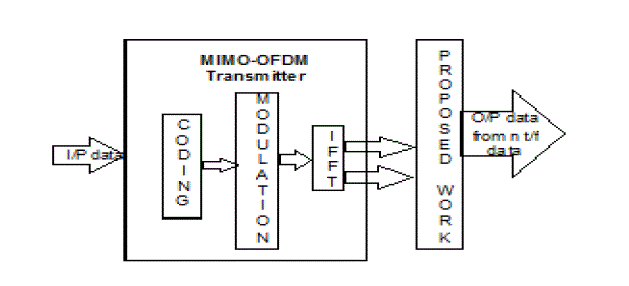
| Above figure describes the MIMO-OFDM-based linear coding system. As shown in Fig.1 the input data will go through a coding stage thus a block of k bits of information data is encoded by a rate r = k/n code. After that, the n coded bits will be modulated to form modulated symbols. Here the modulation scheme is chosen to have QAM constellation. therefore the QAM modulated symbols are formed into blocks of (n/log2)|Ω| QAM symbols and also for PSK. Then to form an OFDM symbol an N-point IFFT stage is used i.e. each OFDM symbol is constructed from Nsub carriers. After the IFFT stage each OFDM symbol will be processed by the proposed technique with two different spreading ratios l, 2 and 3 the final stage is the MIMO block; here in this block the processed signal will be transmitted through transmitter antennas. |
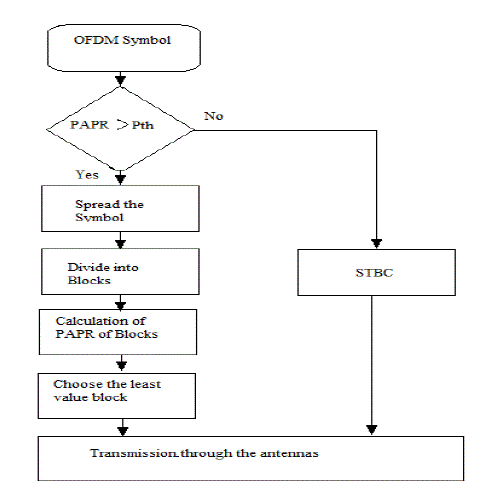
| The reduction of PAPR occurs through a number of stages. Each symbol is passed through the PAPR reduction method and the process is designed so that replications of the symbol is made by means of coding technique and the block which has the lowest value of PAPR will be chosen. The method which has been followed to reduce the PAPR is as follows – |
| Stage 1: Each of OFDM symbols is taken and the guard interval is removed. The PAPR is calculated for the OFDM symbol and if it is lower than a particular threshold, it is passed through the STBC encoder from where it will be directly transmitted through the antennas otherwise; it will pass through the reduction technique. The OFDM symbol is then passed through the coding technique after which it would have spread. This happens because the coding techniques used are linear coding techniques and they increase the symbol period in the time domain. The symbol can also be thought to have been spread according to a spreading rate. Thus, it enables us to have a greater chance of each symbol being checked for the lowest PAPR value. |
| Stage 2: The spread symbols will then be divided into the same number of blocks as the number of antennas. Each block will have the same duration as the original symbol. ThePAPR of each symbol is calculated and the block with the lowest PAPR will be chosen. The guard interval will be added to the chosen symbol and will be combined with the original OFDM signal. Thus, each symbol is checked and the resulting OFDM signal will consist of all symbols with the lowest PAPR. The final OFDM signal will be transmitted through the antennas. |
| Instead of using a number of IFFT’s according to the number of antennas, the MIMO-OFDM system is implemented in such a way that there is only one IFFT and then the division of each OFDM symbol is done in the PAPR reduction method so that the output produces the same number of blocks as the number of antennas. This reduces the complexity at the transmitter side. The block diagram figure1 shows how the PAPR reduction occurs for each symbol of the OFDM signal. The transmission occurs such that each symbol of the OFDM signal after being selected as the block which has the lowest PAPR will be transmitted through one of the antennas and the rest of the blocks will be transmitted through the other antennas. This helps in recovering the original data in case the data through any of the antennas get corrupted |
CONSTRUCTION OF LDPC ENCODER
|
| For an effective encoder-decoder implementation, the parity check matrix has the approximation. and has to be a block structured matrix. There are two main constraints in constructing a good LDPC code: an approximate upper triangular form with as small gap matrix, g, as possible and the block structured matrix feature. Starting from the observation in tackling these constraints, for irregular LDPC codes the variable nodes with high degree tend to converge more quickly than those with low degree. Therefore, with a finite number of decoding iterations, not all the small cycles in the code bipartite graph are equally harmful. In other words, those small cycles that pass more low-degree variable nodes degrade the performance more seriously than others which do not. Thus, it is intuitive that small cycles should be prevented from passing too many low-degree variable nodes. |
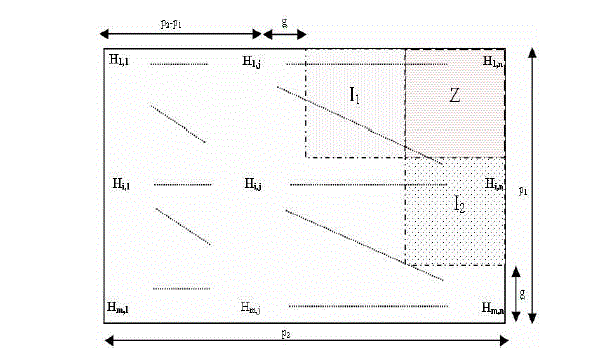
| The size of each block matrix is bxb, the size of parity check matrix is p1xp2, where p1=mb and p2=nb (where m and n define the size of the parity check matrix) g=γb, where γ is the total no of block in the g sub-matrix. The row and column weight distribution are {wr1 , wr2 ,…. , wrn} and {wc1 , wc2 ,…. , wcn} where wriand wcj represent the weight of i- thblock rows and j-th columns, respectively. The output from this parameter will provide the component of the p1xp2 Parity check matrix H. This matrix will be either a right cyclic shift of an identity matrix or a zero matrix. Figure shows the general case structure of the H matrix. I1 and I2 are identity matrix with same size and Z is a zero matrix. The other blocks are initially set as Null blocks. |
| According to the weight distribution of the matrix columns and rows two different set of weight distribution have been generated: |
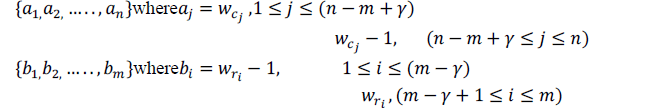 |
 |
 |
| With g=2 and the information vector equals (1,0,0,0,0,0), therefore the code-word is equal to [S1,R1,R2] =[1,0,0,0,0,0,0,1,1,0,1,0] |
SIMULATION RESULT
|
| The simulation results obtained by the implementation of the coding techniques are analyzed in this section. In order to validate our analytically derived technique, the MATLAB Simulation was developed. The simulation environment consist, as anInput image, coding rate is ½, 16QAM modulation technique, IFFT size of 128. The following parameters have been used for the MATLAB simulation of the reduction of PAPR in the MIMO-OFDM system. |
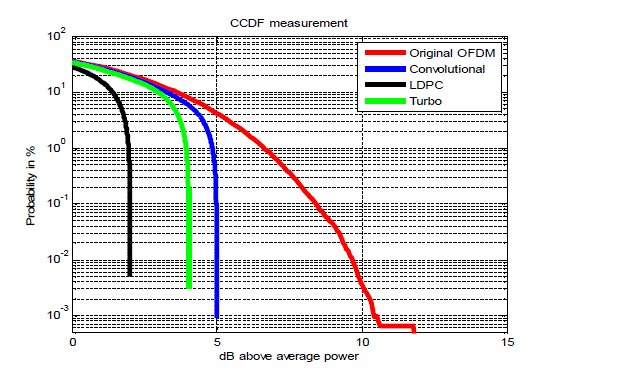
| Table No 1demonstrates that reduction between 20% to 30% in PAPR has achieved when applying LDPC techniques as compared to the other coding techniques like convolutional, turbo coding etc. The CCDF plot for reduction performance with different coding techniques like convolutional, Turbo, & LDPC as shown in figure 4. |
| In figure 4 shows that, the reduction of PAPR using different coding techniques and the PAPR value has decreased significantly from the original value to 5 dB in case of convolutional coding, and to 3.2 dB in case of turbo and to 2.2 dB in case of LDPC coding. |
CONCLUSION
|
| This paper has introduced different types of PAPR reduction techniques. A Low-Density-Parity Check (LDPC) encoder performs effectively in reducing PAPR problem presented in OFDM. And 1.5 to 2 dB reduction in the PAPR has observed by using LDPC. |
Tables at a glance
|
 |
| Table 1 |
|
Figures at a glance
|
 |
 |
 |
 |
| Figure 1 |
Figure 2 |
Figure 3 |
Figure 4 |
|
References
|
- J.Kim and Y.Shin, “An effective clipping companding scheme for PAPR Reduction of OFDM Signal”, IEEE International Conference onCommunications, Beijing 2008.PP 668-672.
- X.B.Wang, “Reduction of Peak-to-Average Power Ratio of OFDM System using a Companding Technique”, IEEE Transaction onBroadcasting. Vol.45. No.3, 1999, PP 303-307.
- Heung–GyoonRyu, Cheng – Xiang Wang,” Nonlinear distortion reduction for the improvement of the BER Performance in OFDMCommunication systems”, ISCIT 2007, PP 67-71.
- I.John, “RBF Neural Network Based SLM Peak-to-Average Power Ratio (PAPR) Reduction in OFDM Systems”, EIRI Journal, Vol. 29, No.3,PP 402-404.
- M.Park, J.Heeyong, N.Cho, D.Hong and C.Karg, “PAPR Reduction in OFDM Transmission using Hadamard Transform”, IEEE InternationalConference on Communications Vol.1. June 2000, PP 430-433.
- Zhongpengwang, “Combined DCT and Companding for PAPR Reduction in OFDM Signals”. Journal of Signal and Information Processing”Vol 2, 2012 PP 100-104.
- Xiaodong Li and Leonard J. Cimini, "Effects of Clipping and Filtering on the Performance of OFDM ," IEEE Communications Letters , Vol. 2,No. 5, May 1998.
- Davis, J. A. and J. Jedwab, “Peak-to-mean power control in OFDM, Golay complementary sequences, and Reed-Muller codes,” IEEE Trans.Information Theory, Vol. 45, 2397–2417, Nov. 1999.
- Wilkison, T. A. and Jones A. E., "Minimization of the Peak to mean Envelope Power Ratio of Multicarrier Transmission Schemes by BlockCoding," IEEE, Vehicular Conference, Vol.2, Jul. 1995.
- Gross, R. and D. Veeneman, “Clipping distortion, in DMT ADSL systems,” IEEE Electron. Lett., Vol.29, 2080–2081, Nov. 1993.
- Jayalath, A. D. S. and C. Tellambura, “Use of data permutation to reduce the peak-to-average power.
- Krongold, B. S. and D. L. Jones, “PAR reduction in OFDM via active constellation extension,” IEEE Trans. on Broadcasting, Vol. 49, 258–268, Sept. 2003.
- Al-Akaidi M., Daoud O., "PAPR Reduction by Linear Coding Techniques for MIMO-OFDM Systems Performance Improvement: Simulationand Hardware Implementation", International Journal of Scientific Researc, vol. 36, no.3, ISSN 1450-216X ,2009.
- Ten Brink, G. Kramer, and A. Ashikhmin, “Design of low-density parity check codes for multi- antennas modulation and detection,” IEEETrans. Commun.,Volume 54,Issue 4.
- Wu Y. and Zou W.Y., "Orthogonal frequency division multiplexing: A multi carrier modulation scheme", IEEE Trans. on ConsumerElectronics, Vol.41, pp.392-399, August, 1995.
- Wunder G., “A theoretical framework for peak-to-average power control problem in OFDM transmission”, PhD thesis, technical UniversityBerlin, 2004.
- Yeo E., Nikolic B., and Anantharam V., “Architectures and Implementation of Low-Density Parity- Check Decoding algorithms,” in 45th IEEEMidwest Symposium on Circuits and Systems, pp. 437– 440, August 2002.
- Zhang T. and Parhi K. K., “Joint (3, k)-regular LDPC Code and Decoder/Encoder Design,” IEEE Transactions on Signal Processing, vol.52, no.4, pp.1065-1079, 2004.
- Saltzberg B. R., “Comparison of Single-Carrier and Multitone Digital Modulation for ADSL Applications,” IEEE Communication Magazine,vol. 36, no. 11 , pp. 114-21, Nov. 1998.
- Tarokh V. and Jafarkhani H., “On the Computation and Reduction of the Peak-to- Average Power Ratio in Multicarrier Communications,”IEEE TransactioCommunications, vol. 48, no.1, pp.37–44, 2000.
- Digital Video Broadcasting Group, “DVB-T2 Call for Technologies”, SB1644 r1, April 2007.
|