Research and Reviews - International Journals

International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Menu

ISSN ONLINE(2278-8875) PRINT (2320-3765)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

Particle Swarm Optimization by Natural Exponent Inertia Weight for Economic load Dispatch

Mohd Javed Khan1, Hemant Mahala2
  1. M.Tech Scholar, Department of Electrical and Electronics Engineering, Oriental Institute of Science and Technology, Bhopal, M.P, India
  2. Associate Professor, Department of Electrical and Electronics Engineering, Oriental Institute of Science and Technology, Bhopal, M.P, India
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Abstract

In this paper ,various inertia weight strategy particle swarm optimization is used to obtain the optimal power dispatch for 6 unit generator system with constraints satisfaction and minimizing the operating cost. The results are compared among classical Particle Swarm Optimization(CPSO),e1PSO, e2PSO methods. The numerical results affirmed the robustness and proficiency of proposed approach over other existing method.

Keywords
E1-PSO, E2-PSO,Economic load dispatch, PSO, Inertia weight, Prohibited operating zones.

INTRODUCTION
The economic load dispatch (ELD) of power generating units has always occupied an important position in the electric power industry. The primary objective of ELD is to schedule the committed generating units output so as to meet the required load demand at minimum cost satisfying all unit and system operational constraints. The optimal ELD should meet load demand, generation limit, ramp rate, prohibited operating zone,[1,2] etc. For solving economic load dispatch various conventional methods like bundle method[3], non linear programming , mixed integer linear programming [4- 7], dynamic programming[5], quadratic programming [6] , Lagrange relaxation method [8], network flow method [9], direct search method [10] are used to solve such problems. When compared with the conventional (classical) techniques[10-11], modern heuristic optimization techniques based on operational research and artificial intelligence concepts, such as evolutionary algorithms [12-13], simulated annealing[14,15], artificial neural networks[16-18], and taboo search [19,20] have been given attention by many researchers due to their ability to find an almost global optimal solution for ELD problems with operation constraints. ELD problem is non linear, non convex type with multiple local optimal point due to the inclusion of valve point loading effect, multiple fuel options with diverse equality and inequality constraints. Dynamic programming method is one of the approaches to solve the non-linear and discontinuous ELD problem, but it suffers from the problem of “curse of dimensionality” or local optimality. Thus the conventional methods have failed to solve such problems as they are sensitive to initial estimates and converge into local optimal solution and computational complexity. Modern heuristic optimization techniques based on operational research and artificial intelligence concepts, such as simulated annealing[14-15], evolutionary programming [13] , genetic algorithm, tabu search [19-20], neural network, particle swarm optimization provides better solution.
The PSO originally developed by Eberhart and Kennedy in 1995[25], is a population based stochastic algorithm. The PSO is an evolutionary optimization tool of swarm intelligence field based on a swarm (population), where each member seen as a particle and each particle is a potential solution to the problem under analysis. Each particle in PSO has a randomized velocity associated to it, which moves through the space of the problem, and implements the simulation of social behavior. PSO however, allows each particle to maintain a memory of the best solution that it has found and the best solution found in the particle’s neighborhood is swarm. The main advantage of PSO algorithm is summarized as: simple concept, easy implementation, robustness to control parameters, and computational efficiency when compared with mathematical algorithms and other heuristic optimization techniques. PSO can be easily applied to nonlinear and non-continuous optimization problem.

ELD PROBLEM FORMULATION
PSO can be formulated as single objective and multi objective problem which are nonlinear and non-convex in nature. Single objective problem can be formulated as Economic Cost Dispatch (ECD) without valve point loading effect[28,30,32]. ECD with valve point loading effect and multiple fuel option (ECD-VPL-MF)[31,32]. Multiobjective formulation includes combined emission economic dispatch CEED [19,14,21], multi-area emission economic dispatch MAEED [29,30], power generation under different utilities [22].

OBJECTIVE FUNCTION
The objective of ELD problem is the minimization of total generation cost considering equality and inequality constraints.

Single objective problem formulation
Followings are under single objective functions.
• Economic cost function
• Economic cost function with valve point loading effect.
The single objective problem can be formulated as fuel cost function or emission of green house gases as an objective function. These equations can be represented as quadratic polynomial of generated power. To get more precise practical results, fuel cost function modified with the inclusion of valve point loading effect and multiple fuel option.

A. SIMPLIFIED ECONOMIC COST FUNCTION
`Simplified economic load dispatch problem can be represented by quadratic function as mentioned in eqn. 1
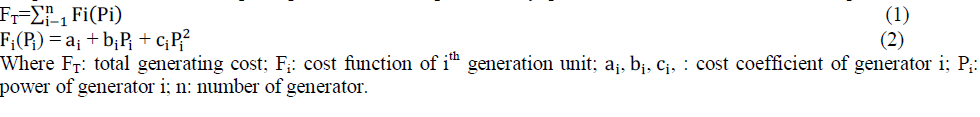image

PARTICLE SWARM OPTIMIZATION (PSO)
Particle swarm optimization is a population based stochastic search algorithm which most recent developments in the category combinatorial meta-heuristic optimization. It was first introduced by Kennedy and Eberhart in 1995 [25] as a new heuristic method. The original objective of their research was to graphically model the social behavior of bird flocks and fish schools. But this original version can only handle the nonlinear continuous optimization problems. Further advancement in this PSO algorithm cam explore the global optimal solution of complex problems of engineering. Amongst various versions of PSO most familiar version was proposed by Shi and Eberhart .The key attractive feature of PSO is its simplicity as it involves only two model Eqs. In PSO, the co-ordinates of each particle represent a possible solution called particles associated with position and velocity vector. At each iteration particle moves toward a optimum solution, through its present velocity, personal best solution obtained by themselves so far and global best solution obtained by all particles. This whole mechanism was based on natural creatures which behave as a Swarm, which exchanges previous experiences among themselves. PSO as an optimization tool provides a population based search procedure in which individuals called particles change their position with time. In a PSO system, particles fly around in a multi dimensional search space. During flight each particles adjust its position according its own experience and the experience of the neighbouring particles, making use of the best position encountered by itself and its neighbours.
In the multi-dimensional space where the optimal solution is sought, each particle in the swarm is moved toward the optimal point by adding a velocity with its position. The velocity of a particle is influenced by three components, namely, inertial, cognitive, and social. The inertial component simulates the inertial behaviour of the bird to fly in the previous direction. The cognitive component models the memory of the bird about its previous best position, and the social components models the memory of the bird about the best position among the particles. The particle moves around the multidimensional search space until they find the optimal solution. The modified velocity of each agent cam be calculated using the current velocity and the distance form Pbest and Gbest as given below.
image
The algorithmic steps involved in particle swarm optimization technique are as follows;
1) Select the various parameters of PSO.
2) Initialize a population of particles with random positions and velocities in the problem space.
3) Evaluate the desired optimization fitness function for each particle.
4) For each individual particle, compare the particles fitness value with its Pbest value, then set this value as the Pbest for agent i.
5) Identify the particle that has the best fitness value. The value of its fitness function is identified as Gbest.
6) Compute the new velocity and positions of the particles according to velocity equation
7) Repeat steps 3-6 until the stopping criterion of maximum generations is met.

STUDY SYSTEM
To assess the efficiency of the proposed pso,it has been applied to ELD problem by considering test system. The data are given by selvakumar and thanushkodi (2007) and Gaing (2003) and are widely used as benchmarks in this field, and are used in many other research groups.
The result obtained by each pso varients are compared with other pso reported in the literature. Case system : The input data of six generator system 26 buses and 46 transmission lines and total demand is set as 1263MW, . The data are as follows
image

TEST RESULTS AND ANALYSIS
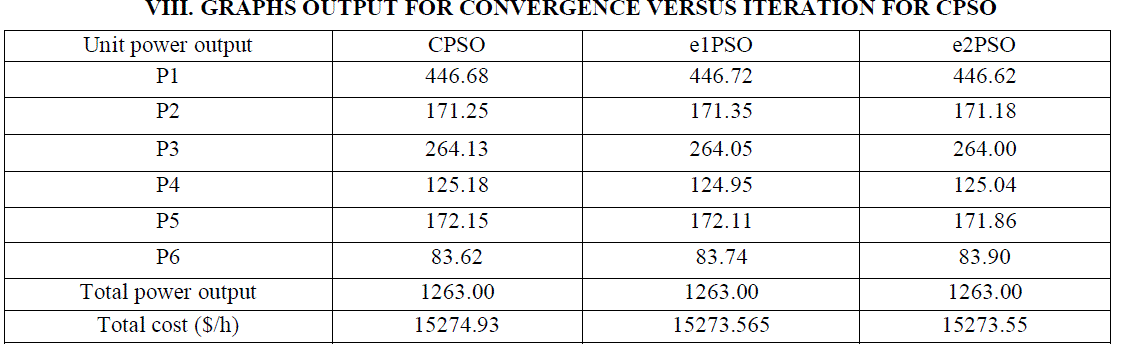
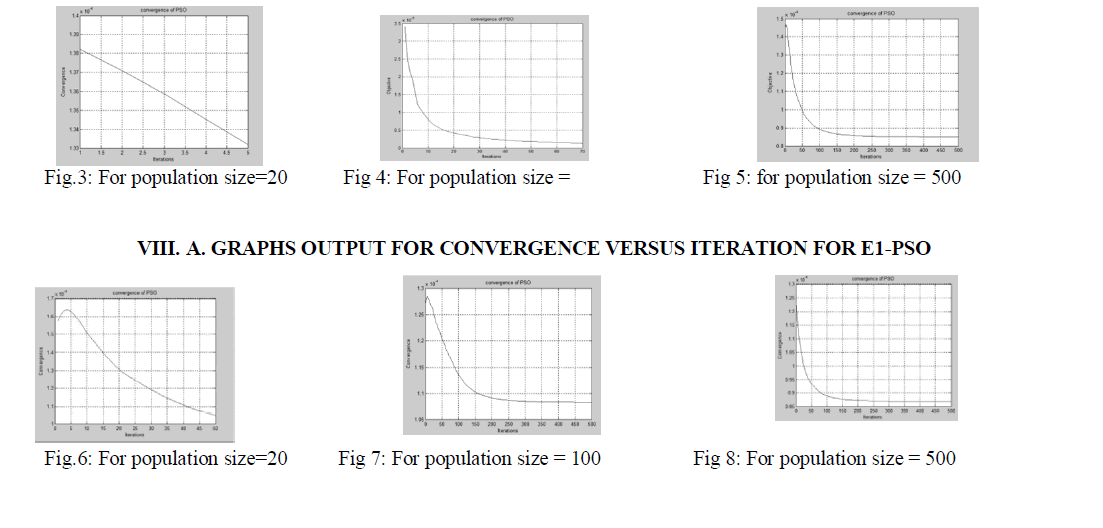
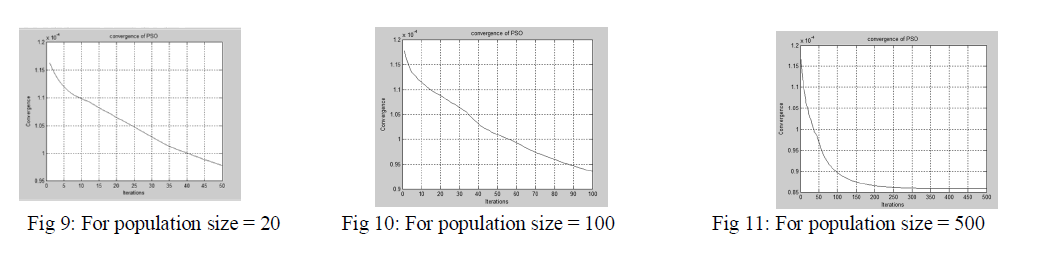
In order to find out effectiveness and superiority of PSO. The test results are compared with the results obtained by each other. To make the results comparable, the same number of population and iterations are used in this paper. The test was carried out in MATLAB software in each case study, 50 independent runs were made for each of the optimization methods. The parameters of CPSO are selected as following: C1=C2=0.01,Wmax=0.9 and Wmin=0.4. The population size was taken different upto 500.

OPTIMAL COST AND GENERATION AT VARIOUS PSO STRATEGY
Table 1. Comparison of various results of output power and their cost of generation using PSO

GRAPHS OUTPUT FOR CONVERGENCE VERSUS ITERATION FOR CPSO
image
image

GRAPHS OUTPUT FOR CONVERGENCE VERSUS ITERATION FOR E2-PSO
image

CONCLUSION
In this paper, an iteration pso algorithm is applied to solve eld problem with cost function with constraints of the prohibited zones. Three variants of pso is applied and results are carried out, which is found to be satisfactory.

References