ISSN ONLINE(2319-8753)PRINT(2347-6710)
ISSN ONLINE(2319-8753)PRINT(2347-6710)
Mr. Dipak L. Patil, Dr. Prakash J. Kulkarni
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology
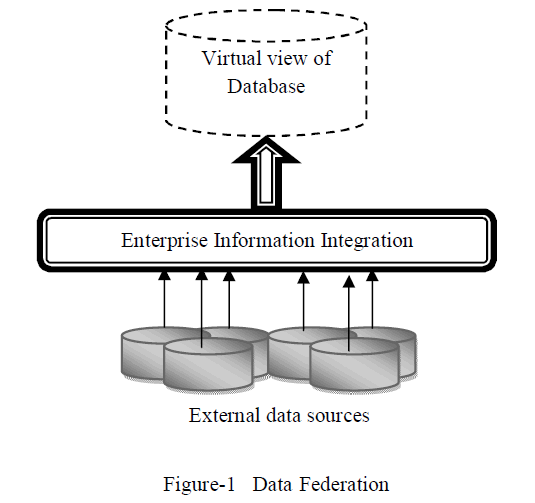
Pattern recognition is important for many computer vision applications such as handwritten character recognition, traffic sign detection, and also it is widely used in the medical field such as detection of retinal vascular bifurcations. In this paper, we are going to propose a new approach for pattern recognition called as a Combination of Shifted Filter Response. It is configured for detecting same and similar pattern. It is configured with the help of prototype pattern provided by the user. It uses a bank of Gabor filters for the edge detection purpose. The output of the Gabor filter is then blurred and shifted with the help of some parameters. All blurred and shifted Gabor responses are then combined with the help of weighted geometric mean. The weighted geometric mean is acts like an AND gate i.e. this will produce output when all the sub parts of a pattern of interest (provided by user) are present. The final result will be the COSFIRE output. It will detect the traffic signs present in the complex scenes. For this, public dataset of traffic sign is used which consist of 48 images. It will detect the traffic sign present in the image. This will helpful to assist the driver during driving or useful for automated vehicle (without driver).
Keywords |
| Pattern recognition, Feature extraction, Gabor filter, Weighted geometric mean, Object recognition |
INTRODUCTION |
| Detection of the keypoint (pattern) feature is an important task in many applications, such as object tracking, image registration, and object recognition.Lots of work has been done in this area and number of methods have been proposed for the pattern detection description and matching of pattern. Keypoint or landmark is not a single point but it refers to a local pattern. The prototype pattern of interest may be a simple edge or corners and junctions. Prototype pattern is specified by the user and same or similar patterns can be detected. This is typically done by computing a similarity (or dissimilarity) measure that is usually based on the Mahalanobis distance, Euclidean distance or some other distance between the respective keypoint descriptors. Due to contrast and texture variations such type of methods are not performed very well and they suffer from inadequate selectivity of the shape properties of features. Previous approaches like Laplacian, Harris detector, are not robust to contrast variations and as a result they suffer from insufficient selectivity to the shape properties of features. |
 |
| The pattern in Fig. 1 which is formed by two lines that make a right-angle vertex is very different from a pattern that is formed by single line, Fig. 1(b). Some approaches that are based on the dissimilarity measure may find these two patterns similar (50%) to a considerable extent. On the other hand, such methods might produce lower similarity scores for patterns that are regarded as similar from the aspect of shape by a human observer, but show differences in contrast and/or contain texture, Figs. 1(c), 2(d). |
| This paper aims towards detection of contour-based patterns. This paper introduces trainable keypoint detection operators that are configured to be selective for given local patterns (given by user) defined by the geometrical arrangement of contour segments [1]. We call the proposed keypoint detector Combination Of Shifted FIlter REsponses (COSFIRE) filter as the response of such a filter in a given point is computed as a function of the shifted responses of Gabor filters (any orientation selective filter may be used). Weighted geometric mean is used to combine filter responses which has specific advantage regarding shape recognition and robustness to contrast variations. Due to the multiplicative character of the weighted geometric mean, a COSFIRE filter produces a response only when all constituent parts of a pattern of interest are present. COSFIRE filter requires the application of selected Gabor filters, Gaussian blurring of their responses, shifting of the blurred responses, and multiplying the shifted responses. |
| Rest of the paper is organized as follows: In section 2, the methodology behind the COSFIRE filter and the essential steps required for COSFIRE filter are explained. In section 3, application of this filter is explained in brief and in section 4, the required datasets that are used in this filter are explained. Finally, we draw conclusion in section 5. |
| The pattern in Fig. 1 which is formed by two lines that make a right-angle vertex is very different from a pattern that is formed by single line, Fig. 1(b). Some approaches that are based on the dissimilarity measure may find these two patterns similar (50%) to a considerable extent. On the other hand, such methods might produce lower similarity scores for patterns that are regarded as similar from the aspect of shape by a human observer, but show differences in contrast and/or contain texture, Figs. 1(c), 2(d). |
| This paper aims towards detection of contour-based patterns. This paper introduces trainable keypoint detection operators that are configured to be selective for given local patterns (given by user) defined by the geometrical arrangement of contour segments [1]. We call the proposed keypoint detector Combination Of Shifted FIlter REsponses (COSFIRE) filter as the response of such a filter in a given point is computed as a function of the shifted responses of Gabor filters (any orientation selective filter may be used). Weighted geometric mean is used to combine filter responses which has specific advantage regarding shape recognition and robustness to contrast variations. Due to the multiplicative character of the weighted geometric mean, a COSFIRE filter produces a response only when all constituent parts of a pattern of interest are present. COSFIRE filter requires the application of selected Gabor filters, Gaussian blurring of their responses, shifting of the blurred responses, and multiplying the shifted responses. |
| Rest of the paper is organized as follows: In section 2, the methodology behind the COSFIRE filter and the essential steps required for COSFIRE filter are explained. In section 3, application of this filter is explained in brief and in section 4, the required datasets that are used in this filter are explained. Finally, we draw conclusion in section 5. |
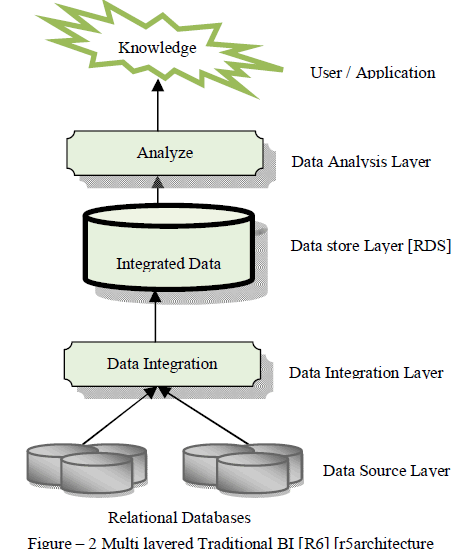
II.PROPOSED METHODOLOGY |
| We are going to propose a filter called as COSFIRE filter. We have to configure this filter with the help of a prototype pattern. And then it will detect the same and similar patterns. |
Overview of the method [1] |
| The fig.2 shows the working of the COSFIRE filter. The Steps involved in the working of the COSFIRE filter are as follows. |
| A) Give the input image to the Gabor filter. |
| B) Gabor response is blurred with Gaussian function |
| C) Shift the blurred responses of each Gabor filter |
| D) Calculate weighted geometric mean The detail explanation of these steps is given as follows. |
A) Give the input image to the Gabor filter |
| A Gabor filter is used for edge detection. The Gabor filter is designed as |
 |
 |
 |
B) Gaussian blur [4] |
| We blur the Gabor filter responses in order to allow for some tolerance in the position of the respective contour parts. A Gaussian blurring is the result of blurring an image by a Gaussian function. Mathematically, applying a Gaussian blur to an image is the same as convolving the image with a Gaussian function. Applying a Gaussian blur has the effect of reducing the image's high-frequency components, a Gaussian blur is thus a low pass filter. |
| The Gaussian blur is a type of image-blurring filter that uses a Gaussian function for calculating the transformation to apply to each pixel in the image. It reduces image noise i. e. it reduces the details of the image. It is similar to smoothing. It preserves boundaries and edges hence it acts as uniform blurring filter. |
C) Shift the blurred responses of each Gabor filter |
 |
D) Geometric mean |
| The specific function that we use here to combine filter responses is weighted geometric mean, essentially multiplication, which has specific advantages regarding shape recognition and robustness to contrast variations. Such a model design decision is mainly motivated by the better results obtained using multiplication versus addition. We can find out other function that gives better result than the weighted geometric mean. If we found, then we can use it for better result. For the geometric mean, we have to multiply responses of all the sub-units and then take nth root where n is number of sub-units. |
III. APPLICATION |
3.1 Detection of Retinal Vascular Bifurcations |
| The DRIVE dataset consist of various images of retinal vascular bifurcations. The fig. 4 is also from the same dataset. It consists of original eye image and the corresponding vascular bifurcation present in the eye image [5]. |
 |
| It consists of 107 blood vessel features which present Y- or T-form bifurcations or cross overs. If we use rotation non-invariant approach for COSFIRE filter then it will detect only 4 TP (True Points). If we use rotation invariant approach then it will detect 24 TP as shown in the fig 5. If we use rotation + scale invariant approach then it will detect 34 TP. If we use rotation + scale + reflection invariant approach then it will detect 67 TP as shown in the Fig. 6. |
 |
IV. lDATA SET |
| Several datasets are used for performing experiments on COSFIRE filter for analyzing the performance of the COSFIRE filter. Some of them are DRIVE data set, MNIST data set, etc. |
A)Public dataset |
| The detection and recognition of specific objects in complex scenes is one of the most challenging tasks in computer vision. COSFIRE filters can be used for the detection of traffic signs in complex scenes. We use a public dataset of 48 color images (of size 360 x 270 pixels) that was originally published in [11]. |
B)DRIVE data set |
| Digital Retinal Images for Vessel Extraction (DRIVE) data set is used for detection of retinal vascular bifurcations. The DRIVE database has been established to enable comparative studies on segmentation of blood vessels in retinal images. The photographs for the DRIVE database were obtained from a diabetic retinopathy screening program in The Netherlands. Forty photographs have been randomly selected. The set of 40 images has been divided into training and a test set, both containing 20 images [5]. |
C)MNIST data set |
| The MNIST Dataset contains 70,000 images of handwritten digits (zero through nine), divided into a 60,000-image training set and a 10,000-image testing set. It is a good database for people who want to try learning techniques and pattern recognition methods on real-world data while spending minimal efforts on preprocessing and formatting [6]. |
V. CONCLUSION |
| The filter output is computed as the product of blurred and shifted Gabor filter responses. Gabor filters are very useful for line detection, hence bank of Gabor filters is used to detect lines and blurred and shift parameters also. They are versatile detectors of contour related features as they can be trained with any given local contour pattern and are able to detect identical and similar patterns [1]. It has many practical applications such as detection of retinal vascular bifurcation, recognition of handwritten digits as well as characters also, detection and recognition of traffic signs etc. |
ACKNOWLEDGMENT |
| I would like to express my sincere thanks to all those who helped me directly or indirectly in this esteemed work. |
References |
|