Keywords
|
| enhanced, multispectral, Palm print, PCA, weighted. |
I. INTRODUCTION
|
| Fusion is a good way to increase the system accuracy and robustness. The image fusion method tries to solve the problem of combining information from several images taken from the same object to get a new fused image. Multisensor image fusion is the process of combining information from two or more images into a single image. The resulting image contains more information as compared to individual images. |
| Hand biometrics including fingerprint, palm print, hand geometry and vein pattern has extensive attention in recent years. Multispectral palm images have richer and denser pattern for recognition. Palm print is a unique and reliable biometric characteristic with high usability. With the increasing demand of highly accurate and robust palm print authentication system, multispectral imaging has been used. One solution to these problems can be multispectral imaging, which captures an image in a variety of spectral bands. Each spectral band has specific features of the palm that collect more information to improve the accuracy and anti-spoofing capability of palm print systems. As Per Author David Zhang From the Hong Kong Polytechnic University,[16] Different light wavelength will penetrare to different skin layer and illumination in different spectra. Near Infrared (NIR) light penetrates human tissues further than visible light, and blood absorbs more NIR energy than surrounding tissues .The device acquire spectral information from all three dermal layers by using both visible band and NIR band. In the visible spectrum, a three monocolor LED arrey is used with Red peaking at 660 nm, Green at 525nm, Blue at 470nm. In NIR LED array peaking at 880nm is used.It has shown that light in the 700-1000nm range can penetrate human skin while 880-930nm provide a good contrast of subcutaneous veins. It can observe those line features are clearer in Blue and Green band than in the RED and NIR bands. while the RED band can reveal some vein structures, the NIR band can show palm vein structures as well as partial line information .Fusion of blue and and NIR could get better accuracy. Fusion of Green and NIR is better than Green , but a little inferior than NIR. The remaining fails to improve the accuracy than single spectrum. Blue and NIR , Green and NIR have less correlation, so their fusion could get better result than other combination. Blue and Red , Green and Red ,and Red and NIR have medium correlation, their fusion get worse result . Blue and Green has the large correlation while medium fusion accuracy. Thus, a less correlation fusion strategy is preferred. |
| [1] In this paper, authors propose a palmprint recognition method based on eigenspace technology. By means of the Karhunen–Loeve transform, the original palmprint images are transformed into a small set of feature space, called ‘‘eigenpalms’’, which are the eigenvectors of the training set and can represent the principle components of the palmprints quite well. Then, the eigenpalm features are extracted by projecting a new palmprint image into the subspace spanned by the ‘‘eigenpalms’’, introduction to eigenpalms feature extraction and presented an efficient method to calculate the eigenvectors and eigenvalues and applied to palmprint recognition with a Euclidean distance classifier. Experimental results illustrate the effectiveness of our method in terms of the recognition rate. [2]In this paper, proposes a novel technique for palmprint recognition in the transform domain and based on a combination of Principal Component Analysis (PCA) and Fourier transform. Although, PCA is widely adopted as one of the most promising tools for use in biometric recognition systems,it comes with its own limitations: poor discriminating power in the presence of variant illuminations, requires a large computational load when the original dimensionality of data is high while the number of training samples is usually large. Traditionally, to represent the palmprint image, PCA is carried out on the whole spatial image.In this paper, an efficient palmprint recognition approach called eigenspectra is proposed. The idea behind eigenspectra is to find a lower dimensional space in which shorter vectors will describe palmprint images more accurately.The PCA is performed on the Fourier spectrum coefficients to compute and capture those eigenspectra components that maximize the energy of the palmprint images. [4]This paper presents a method of representing the multispectral palmprint images by quaternion and extracting features using the quaternion principal components analysis (QPCA) to achieve better performance in recognition. A data acquisition device is employed to capture the palmprint images under Red, Green, Blue and near-infrared (NIR) illuminations in less than 1s. QPCA is used to extract features of multispectral palmprint images. In this paper, use quaternion to represent multispectral palmprint images and apply quaternion principal components analysis (QPCA) to extract features, and then do the recognition.From experimental result Table,see that the NIR and Red bands have higher recognition rate than the Blue and Green Bands, that’s because the NIR and Red bands can capture more features such as the vein features. The recognition rate of the Red band is higher than the recognition rate of NIR bands because the palm lines in the Red band images are clearer than those in the NIR band. The recognition rates of the Green and Blue bands are very similar. [8] In this study, propose a new method for multispectral images based on a quaternion model which could fully utilize the multispectral information. Firstly, multispectral palmprint images captured under red, green, blue and near-infrared (NIR) illuminations were represented by a quaternion matrix, then principal component analysis (PCA) and discrete wavelet transform (DWT) were applied respectively on the matrix to extract palmprint features. In this paper and to fully utilize the information of multispectral palmprint images, to the best of our knowledge, a quaternion model is employed for multispectral biometrics for the first time. QPCA is proposed for representing global features while QDWT is designed for extracting local features. The special arrangement has shown that the quaternion matrix is still effective for multispectral palmprint in the situation with less than four illuminations. [5]In this paper, propose palmprint identification using Transform Domain and Spatial Domain Techniques (PITS). The histogram equalization is applied on each image to distribute intensity values uniformly.Histogram equalization is used on palmprint to enhance contrast of an image. The Haar wavelet is used on the histogram equalized image to generate low frequency band i.e., approximation band and high frequency bands . The DWT is applied on Histogram equalized image to generate LL, LH, HL and HH bands. The LL band is converted into DCT coefficients using DCT. QPCA is applied on DCT coefficients to generate features. The test and database palmprint features are compared using Euclidean Distance (ED). It is observed that the proposed method gives better performance compared to existing method. [6]The paper presents PCA based image fusion to improve resolution of the images in which two images to be fused are firstly decomposed into sub-images with different frequency and then the information fusion is performed and finally these sub-images are reconstructed into a result image with plentiful information. The PCA algorithm builds a fused image of several input images as a weighted superposition of all input images. PCA-based image fusion is adopted to obtain the palmprint with improved resolution for higher reliability. Multiple features were extracted from this palmprint containing enhanced information. The discriminative powers of different feature combinations were analyzed and we find that density is very useful for palmprint recognition. Hence, the multi-image fusion with PCA extraction of multiple features for palmprint recognition significantly improves the matching accuracy. [7]This paper studied the correlation based on Spearman correlations coefficient. If the matrix reflects a strong correlation, this fusion strategy should be a failure. We test two fusion strategies in experiment. A) Feature vectors extracted by principle components analysis method (PCA) plus feature vectors extracted by PCA method from images after DCT transform. B) Feature vectors extracted by PCA method plus feature vectors extracted by independent components analysis (ICA) method. Experimental results show that strategy B brings an improved performance, for the features vectors in this strategy with weak correlation [10]In this paper, we propose a PCA-based spectral band compression and multispectral palmprint recognition method. This method first exploits PCA to compress original multispectral bands to a smaller number of ‘bands’ and then uses the compressed bands to classify palmprint images. The proposed method has the following rationale: as PCA is able to eliminate the correlation between different multispectral palmprint images, the method can use a few data to represent the original multispectral palmprint images. Moreover, as the method uses PCA to generate the most representative data of the original multispectral images, it can use much more information to perform palmprint recognition than previous methods, which selected only a small number of spectral bands for ultimate multispectral palmprint recognition. In previous literature, different spectral bands highlight different texture information of the palmprint, so the fusion of them is useful to reduce the error rate of classification. On the other hand, we see that for the same palm different spectral bands also contain redundant information. Actually, the closer the central wavelengths of two bands, the more the redundant information. PCA is the most effective decorrelation method and can transform original data into the most representative uncorrelated components, so it is able to use less data to represent the original multispectral images. Thus, we also say that our method can transform original spectral bands into the most representative uncorrelated data that has a few components. Our method can do so owing to the PCA’s ability of transforming original data into the most representative uncorrelated components. As a result, our method has the potential to obtain a higher accuracy. The experimental results show that our proposed PCA-based spectral band compression and recognition method can use very low dimensional data to represent the original multispectral palmprint images and obtain a high classification accuracy. |
| In this paper, presents PCA based image fusion to improve resolution of the images in which two images to be fused are firstly decomposed into sub-images with different frequency and then the information fusion is performed and finally these sub-images are reconstructed into a result image with plentiful information. This paper presents assessment of image fusion by measuring the quantity of enhanced information in fused images. |
II. PRINCIPAL COMPONENT ANALYSIS
|
| PCA (Principle Component Analysis is widely used in image processing, especially in image compression. Also, it is called the Karhunen-Leove transform KLT or the Hotelling transform. Principal components analysis PCA is a statistical procedure that allows finding a reduced number of dimensions that account for the maximum possible amount of variance in the data matrix. The PCA basis vectors are the eigenvector of the covariance matrix of the input data. This is useful for exploratory analysis of multivariate data as the new dimensions called principal components PCs. A reduced dimension can be formed by choosing the PCs associated with the highest eigenvalues. So, we can consider KLT as a unique transform which decorellates its input. Calculating a principal components analysis is relatively simple and depends on some characteristics associated with matrices eigenvalues and eigenvectors. To calculate the PCA we first estimate the correlation matrix or covariance matrix of the image array. The next step is to calculate the eigenvalues of the matrix. Each eigenvalue can be interpreted as the variance associated with a single vector. The next step is to calculate the eigenvectors associated with each eigenvalue. Each eigenvector represents the factor loading associated with a specific eigenvalue. By multiplying the eigenvector by the square root of the eigenvalue. This is all the information we need to begin to apply PCA. Finally, we need to select the number of eigenvectors needed to explain the majority data of the image. We simply select the eigenvectors associated with the largest eigenvalues to represent a sufficient amount of the image data. |
| A. Characteristics Of Principal Component |
| The first component extracted in a principal component analysis accounts for a maximal amount of total variance in the observed variables. Under typical conditions, this means that the first component will be correlated with at least some of the observed variables. It may be correlated with many. |
| The second component extracted will have two important characteristics. First, this component will account for a maximal amount of variance in the data set that was not accounted for by the first component. Again under typical conditions, this means that the second component will be correlated with some of the observed variables that did not display strong correlations with component 1. |
| The second characteristic of the second component is that it will be uncorrelated with the first component. Literally, if you were to compute the correlation between components 1 and 2, that correlation would be zero. The remaining components that are extracted in the analysis display the same two characteristics: each component accounts for a maximal amount of variance in the observed variables that was not accounted for by the preceding components, and is uncorrelated with all of the preceding components. |
| A principal component analysis proceeds in this fashion, with each new component accounting for progressively smaller and smaller amounts of variance (this is why only the first few components are usually retained and interpreted). When the analysis is complete, the resulting components will display varying degrees of correlation with the observed variables, but are completely uncorrelated with one another. |
| B. Eigenpalm: feature extraction |
| Palmprint image is described as a two-dimensional array (NxN). In the eigenspace method, this can be defined as a vector of length N2, called a ‘‘palm vector’’. A sub palmprint image is fixed with a resolution of 128x 128, hence a vector can be obtained, which represents a single point in the16,384-dimensional space. Since palmprints have similar structures (usually three main lines and creases), all ‘‘palm vectors’’ are located in a narrow image space, thus they can be described by a relatively low dimensional space. As the most optimal orthonormal expansion for image compression, the K–L transform can represent the principle components of the distribution of the palmprints or the eigenvectors of the covariance matrix of the set of palmprint images. Those eigenvectors define the subspace of the palmprints, which are called ‘‘eigenpalms’.[1] The idea behind eigenpalm is to find a lower dimensional space in which shorter vectors will describe palmprint images more accurately. Principal Component Analysis (PCA) is employed to transform original image to its eigenspace. By retaining the principal components with influencing eigenvalues, PCA keeps the key features in the original image and reduces noise level. In Principal Component Analysis (PCA) is a vector space transform often used to reduce multidimensional data sets to lower dimensions for analysis. It reveals the internal structure of data in an unbiased way. Principal component Analysis is a mathematical tool which transforms a number of correlated variables into a several uncorrelated variables. PCA is widely used in image classification. The PCA image fusion method simply uses the pixel values of all source image at each pixel location, add a weight factor to each pixel, and takes an average of the weighted pixel values to produce the result for the fused image at the same pixel location. The optimal weighted factors are determined by the PCA techniques. |
| The PCA technique is useful for image encoding, image data compression, image enhancement, pattern recognition (especially for object detection), and image fusion. It is a statistical technique that transforms a multivariate data set of inter-correlated variable into a data set of new un-correlated linear combinations of the original variables. It generates a new set of axes which is orthogonal. By using this method, the redundancy of the image data can be decreased. |
| The PCA-based image fusion technique adopted here improve resolution of the images in which images to be fused are firstly decomposed into sub images with different frequency and then the information fusion is performed and finally these sub images are reconstructed into a result image with plentiful information. The PCA algorithm builds a fused image of several input images as a weighted superposition of all input images. The resulting image contains enhanced information as compared to individual images. This image is used for palmprint recognition. Multiple features like minutiae, density map, and principal line map are reliably extracted and combined to provide more discriminatory information. The presence of a large number of creases is one of the major challenges in reliable extraction of the ridge information. Creases break the continuity of ridges, leading to a large number of spurious minutiae. Moreover, in regions having high crease density, the orientation field of the ridge pattern is obscured by the orientation of creases as it changes with season. Also the density map feature is proved to be a good supplement to minutiae for palmprint recognition.[6] |
| The most straightforward way to build a fused image of several input images is performing the fusion as a weighted superposition of all input images. The optimal weighting coefficients, with respect to information content and redundancy removal, can be determined by a principal component analysis of all input intensities. By performing a PCA of the covariance matrix of input intensities, the weightings for each input image are obtained from the eigenvector corresponding to the largest eigen value. The weights for each source image are obtained from the eigenvector corresponding to the largest eigen value of the covariance matrices of each source. |
| C. PCA Algorithm |
| Let the source images (images to be fused) be arranged in two-column vectors. The steps followed to project this data into a 2-D subspaces are: |
| The most straightforward way to build a fused image of several input images is performing the fusion as a weighted superposition of all input images. The optimal weighting coefficients, with respect to information content and redundancy removal, can be determined by a principal component analysis (PCA) of all input intensities. By performing a PCA of the covariance matrix of input intensities, the weightings for each input image are obtained from the eigenvector corresponding to the largest eigenvalue.[6] |
| Arrange source images in two-column vector. |
| 1) Organize the data into column vector. Let S be the resulting column vector of dimension 2 X n. |
| 2) Compute empirical mean along each column. The empirical mean vector Me has a dimension 1X2. |
| 3) Subtract Me from each column of S. The resulting matrix X is of dimension 2 X n. |
| 4) Find the covariance matrix C of matrix X i.e. C=XX T mean of expectation = cov(X). |
| 5) Compute the eigenvectors V and eigenvalue D of C and sort them by decreasing eigenvalue. Both V and D are of dimension 2 x 2. |
| 6) Consider first column of V which correspond to larger eigenvalue to compute normalized component P1 and P2. |
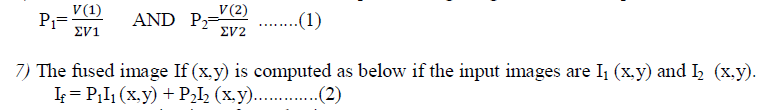 |
| Hence, Image Fusion is performed using PCA. |
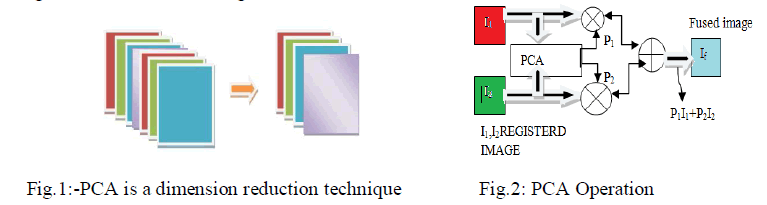
| The information flow diagram of PCA-based image fusion algorithm is shown in Fig.1 The input images (images to be fused) I1 (x, y) and I2 (x, y) are arranged in two column vectors and their empirical means are subtracted. The resulting vector has a dimension of n x 2, where n is length of the each image vector. Compute the eigenvector and eigenvalues for this resulting vector are computed and the eigenvectors corresponding to the larger eigenvalue obtained. The normalized components P1 and P2 (i.e., P1 + P2 = 1) using Eqn (1) are computed from the obtained eigenvector. The fused image is: |
 |
| D. PCA Advantages |
| PCA’s key advantages are its low noise sensitivity, the decreased requirements for capacity and memory, and increased efficiency given the processes taking place in a smaller dimensions; the complete advantages of PCA are listed below: |
| 1) Lack of redundancy of data given the orthogonal components . |
| 2) Reduced complexity in images grouping with the use of PCA |
| 3) Smaller database representation since only the trainee images are stored in the form of their projections on a reduced basis |
| 4) Reduction of noise since the maximum variation basis is chosen and so the small variations in the back-ground are ignored automatically [9]. |
III. MULTISPECTRAL PALMPRINT DATABASE
|
| Experiment is performed on multispectral PolyU (Hong Kong Polytechnic University). The Biometric Research Centre (UGC/CRC) at The Hong Kong Polytechnic University has developed a real time multispectral palm print capture device which can capture palm print images under blue, green, red and near-infrared (NIR) illuminations, and has used it to construct a large-scale multispectral palm print database “Blue.rar”, "Green.rar", "Red.rar" and "NIR.rar" contains all the original palm print images collected by our device by blue, green, red and NIR illumination [12]. In this paper, from all database only 60 images for Red, Green, Blue and NIR have used for experimentation. |
IV. PERFORMANCE EVALUTION OF IMAGE FUSION
|
| The widespread use of image fusion methods, in military applications, in surveillance, in medical diagnostics, etc., has led to an increasing need for pertinent performance or quality assessment tools in order to compare results obtained with different algorithms or to obtain an optimal setting of parameters for a given fusion algorithm. |
| A. Structural similarity index (SSIM) |
| Structural similarity index (SSIM) represents perceptual image quality based on the structural information. SSIM is an objective image quality metric and is superior to traditional quantitative measures such as MSE and PSNR. The structural similarity (SSIM) index is a method for measuring the similarity between two images. The SSIM index can be viewed as a quality measure of one of the images being compared provided the other image is regarded as of perfect quality. |
| Natural image signals would be highly structured and their pixels reveal strong dependencies. The dependencies would carry vital information about the structure of the object. It compares local patterns of pixel intensities that have been normalized for luminance and contrast. |
 |
| B. EDGE based QABF |
| It is an index of edge information preservation. by evaluating the amount of edge information that is transferred from input image, a measure of performance can be obtained. |
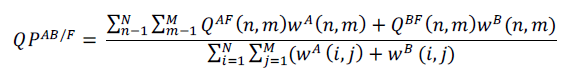 |
| Where edge preservation values, QAF(n,m) and QBF(n,m) ,are weighted by wA (n,m) and w (n,m) respectively. In general preservation values which correspond to pixels with higher edge strength should influence Q p AB/F more than those of relatively low edge strength. |
V. PCA BASED MULTISPECTRAL PALM IMGES
|
 |
| VI. RESULT |
 |
 |
 |
VII. CONCLUSION AND FUTURE WORK
|
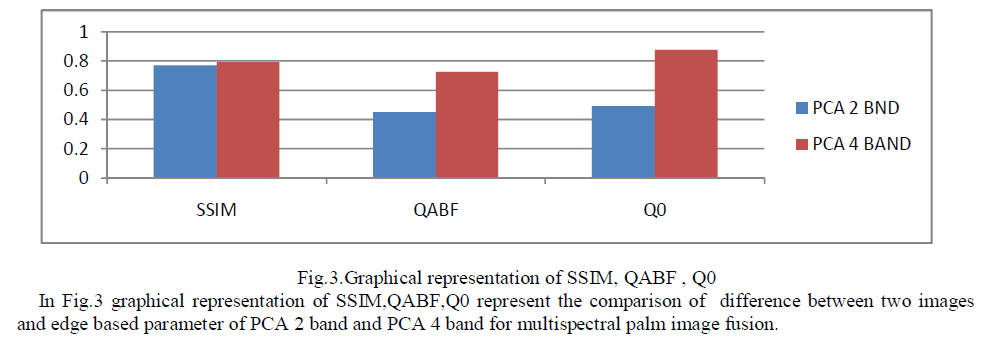
| Palm print images from multiple spectrum is combined. Images from red, green, blue and NIR spectrum are taken. It is focusing on the methods of Image fusion namely Principal component analysis (PCA) between the two band, i.e. Blue and Nir and four band i.e. Red, green, blue, Nir. The POLYU database is used for this experiment. The different Red, Green, Blue and NIR images of palm are fused here. In this paper, it presents that the idea of multispectral palm image fusion for biometrics. In this work an efficient palmprint authentication system based on the fusion of multispectral palm images has been used. It is known that standard deviation is composed of the signal and noise parts. This metric would be more efficient in the absence of noise. It measures the contrast in the fused image. From the above table Standard deviation (SD) of PCA 2 band is 84.856 and PCA 4 BAND is 92.43. In PCA 4 band measure more contrast as compare to 2 band PCA. |
| Entropy is used to measure the information content of an image. Entropy is sensitive to noise and other unwanted rapid fluctuations. An image with high information content would have high entropy. From above, it's clear 4 band PCA gives more information as compared to 2 bands. From entropy result, it clear that SD gives the right result. The structural similarity metric describes differences between two images by means of three variables luminance, contrast, and spatial similarity, which show the better evaluating capability than others objective metrics. A measure of structural similarity (SSIM) that compares local patterns of pixel intensities that have been normalized for luminance and contrast. SSIM is a full reference quality measure that measures the similarity between images. It is the efficient metric and is the improved one than PSNR and MSE. In PCA 2 Band SSIM IS 0.770 AND PCA 4 band 0.790. In PCA 4 band SSIM gives quite good as compared to 2 band PCA. Also edge based parameter Q0 and QABF give good result in 4 band PCA.The PCA method is an unsupervised technique of learning that is mostly suitable for databases that contain images with no class labels. As mentioned above, the PCA method’s advantages have also been explained in this study. |
References
|
- G. Lu, D. Zhang, K. Wang “Palmprint Recognition Using Eigenpalms Features” Pattern Recognition Letters 24 (2003) 1463–1467.
- MoussadekLaadjel, Ahmed Bouridane And FatihKurugollu “EigenspectraPalmprint Recognition” 4th IEEE International Symposium OnElectronic Design, Test & Application
- W. Zuo, D. Zhang, Senior Member, Ieee, And K. Wang, Member, Ieee “Bidirectional Pca With Assembled Matrix Distance Metric For ImageRecognition” Ieee Transactions On Systems, Man, And Cybernetics—Part B: Cybernetics, Vol. 36, No. 4, August 2006.
- X. Xu, Z. Guo “ Multispectral Palmprint Recognition Using Quaternion Principal Component Analysis” ©2010 IEEE
- K P Shashikala , K. B. Raja “Palmprint Identification Using Transform Domain And Spatial Domain Techniques” 2012 InternationalConference On Computing Sciences.
- N. Joshitha J, R. MedonaSelin “ Image Fusion Using PCA In Multifeature Based Palmprint Recognition” International Journal Of SoftComputing And Engineering (IJSCE) ISSN: 2231-2307, Volume-2, Issue-2, May 2012
- Y.Caimao, S. Dongmei, L. Di, C.Yeung And Z.Yanqiang “A Research On Feature Selection And Fusion In Palmprint Recognition” ©2010IEEE
- X. Xu , Z. Guo *, C. Song 3 And Y.Li “Multispectral Palmprint Recognition Using A Quaternion Matrix” Sensors 2012, 12, 4633-4647;Doi:10.3390/S120404633
- S. karamizadeh, s. abadhulla “ An Overview of Principal Component Analysis” Journal of Signal and Information Processing, 2013,4, 173-175
- Y. Xu* Qi Zhu, “PCA-Based Multispectral Band Compression And Multispectral Palmprint Recognition” 978-1-4577-0490-1/11/$26.00©2011 IEEE
- Y. Caimao, S. Dongmei, L. Di,C.Yeung And Z.Yanqiang, “A Research On Feature Selection And Fusion In Palmprint Recognition” 978-1-4244-7065-5/10/$26.00 ©2010 IEEE
- Http://Www.Comp.Polyu.Edu.Hk/Biometrics
- S. S. Bedi, R. Khandelwal, “ Comprehensive And Comparative Study Of Image Fusion Techniques” International Journal Of Soft ComputingAnd Engineering ISSN: 2231-2307, Volume-3, Issue-1, March2013.
- Sonal, D. Kumar, “A Study Of Various Image Compression Techniques”
- D.zhang, W. kong , J.You , M. wong , “ Online palmprint identification” IEEE transcation on pattern analysis and machine Intelligence, vol .25,pp.1041-1050,2003.
- D. Zhang, Fellow, IEEE, Z. Guo, G. Lu, Lei Zhang, Member, IEEE, and W. Zuo, “An Online System of Multispectral PalmprintVerification”IEEE transactions on instrumentation and measurement, vol. 59, no. 2, february 2010.
|