Research and Reviews - International Journals

International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Menu

ISSN ONLINE(2278-8875) PRINT (2320-3765)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

Performance Analysis of SMQW SOA Based On Optical Confinement Factor

Nipu R. Barai1, Rinku Basak2
  1. M.Sc. Student, Dept. of Electrical and Electronic Engineering, American International University-Bangladesh, Dhaka
  2. Assistant Professor and Head of Graduate Program, Faculty of Engineering, American International University- Bangladesh, Dhaka, Bangladesh
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Abstract

Study of the dependency of optical confinement factor (OCF) on the structure parameters of symmetrical multiple quantum well (SMQW) semiconductor optical amplifier (SOA) is important for better design of SOA devices. This paper presentsan overall structure of a SMQWSOA, and dependency analysis of OCF on different structure parameters.The effects of number of well layers, well thickness and barrier thickness of SMQW SOA on OCF are investigated through simulations performed using MATLAB.The simulation results show that OCF of a SMQW SOA increases with increasing number of quantum well layers and well layer thickness. However, the change in barrier thickness doesn‟t have significant impact on the OCF.Thesimulation resultsalso indicate that with appropriate number of well layers and well layer thickness, it is possible to obtain a better OCF.The findings of this study can be used for creating more efficient and stable SMQW SOA design.

Keywords
Symmetrical Multiple Quantum-well, Semiconductor Optical Amplifier, Optical Confinement Factor.

INTRODUCTION
Semiconductor optical amplifier, referred to as SOA, is used for many applications in all-optical systems including amplification of the optical signal without converting it into electrical signal [1].SOA is becoming popular because it is suitable for integration and it can be used as functional devices.In addition, it can operate in a wide bandwidth region. There are many types of SOA depending on the construction of its active region (e.g., multiple quantum well (MQW) SOA,travelling wave (TW) SOA, quantum dot (QW) SOA, gain clamped (GC) SOA)[2-3].Based on the quantum well layers MQW SOA can be divided into two types,thesymmetrical MQW SOA and the asymmetrical MQW SOA. Symmetrical multiple quantum well (SMQW) SOAis the focus point of this paper. The structure of SMQW SOA is similar to that of a semiconductor laser. The main difference is in the anti-reflective mirror (or coating) on both of its facets [4]. The fabrication of the active region is done by loading well and barrier layers. These layers are grown using different types of growth technique such as molecular beam epitaxy (MBE), organo-mettalic vapour epitaxy (OMVPE) [2]. The advantages of using SMQW SOA are its ability to perform at original to ultra-long wavelength band, higher saturation output, ultrafast gain recovery, low noise operation, control polarization sensitivity, compactness, and costeffectiveness [5-7]. Some of the drawbacks include narrower full width half maximum (FWHM) gain bandwidth and complexity in growing layers [8-9].
For performance analysis and comparison with other types of SOAs, a clear understanding of the dependency onvarious factors is necessary for SMQW SOA.One of these factors is the optical confinement factor (OCF). The dependency of OCF on the number of layers and layer thicknesses is important forthe performance analysis of the device. The performance analysis is also important for designing boththe SMQW SOA andASMQW SOA, andfor the comparison of their performances. In addition, the analysis of the dependency of saturation power on the structure parametersis also useful. Therefore, the main objective of this work is to analyse the dependencies of OCF on SMQW SOA structure parameters by performing computer simulations.

THEORETICAL BACKGROUND
A simplified schematic structure of 3D SMQW SOA is shown in Fig. 1. It shows the wells and barrier layers of the active region, as well as the cladding layers. In this case, it is considered that the active region length is equal to the cavity length, and the taper length, Lt, isequal to zero. The length of the active region (L) is given by [11],
image
where, Lc is the cavity length. The amplifier is designed with negligible facet reflectivity to ensure a single pass.
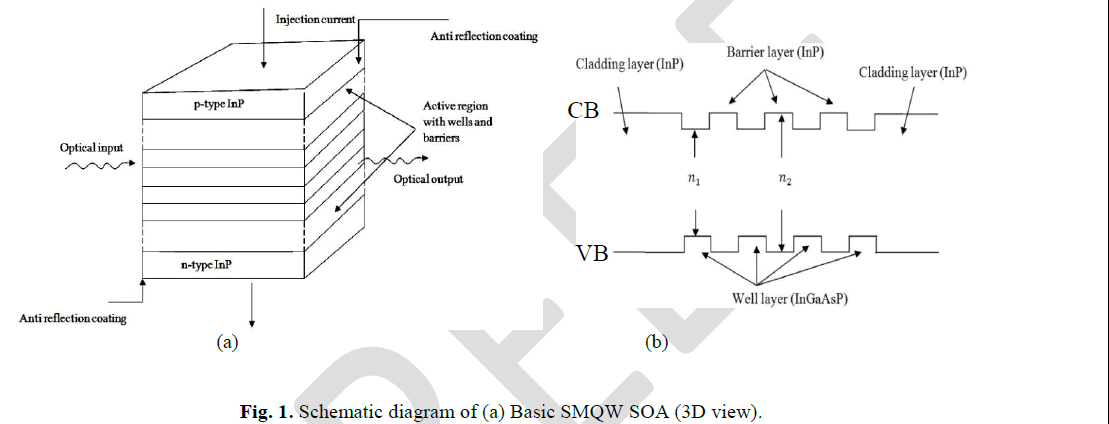image
Injection current direction and power direction is shown. Length of the active region is considered to be equal to the length of the cavity region and the taper length is ignored. The active region is sandwiched between the two doped cladding layers and the number of wells and barrier layers can be varied according to the need of the application. (b) Basic structure of the conduction band (CB) and valence band (VB) of a SMQW SOA where the cladding and barrier material is InP and the well material is InGaAsP. Here ��1 and ��2 are refractive indices of the well and barrier layers and (��1>��2).
The injection current (I) is related to the carrier density (n) by [12],
image
where, q is the electron charge, V is the volume of the active region, n is the carrier density and τc is the carrier lifetime. Carrier lifetime is non linearly dependent to the Auger nonradiative recombination in InGaAsP material system as [13],
image
where, Anr is nonradiative recombination coefficient, B is the bimolecular radiative recombination coefficient and C is the Auger non radiative recombination coefficient.
The saturation power dependency on the material parameters can be expressed as [12],
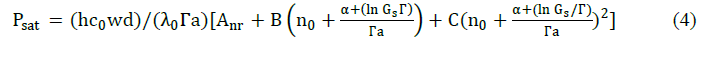image
image
where, n is the carrier density, n0 is the carrier density for transparency, Γ is the optical confinement factor, α is the insertion loss, a is the material gain co-efficient, h is the Planck‟s constant, c0 is the speed of light in vaccum and λ0 is 1.55 μm. OCF is related to the active layer parameters and refractive indices of the layer materials [2].
image
where, Nw is the number of wells, Nb is the number of barriers denoted by (Nw − 1), dw is the well thickness, db is the barrier thickness, μw is the refractive index of the well layer material (InGaAsP in this case), μb is the refractive index of the barrier material ( here,InP). Substitutionof the value of equation (9) into equation (8) provides,
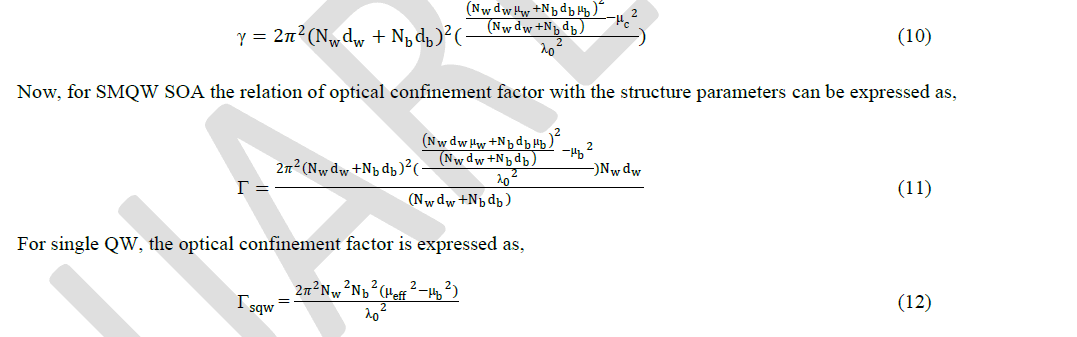image
OCF is the ratio of light intensity within the active region to the total light intensity. It is defined as „Γ‟. As the name indicates, the light is needed to be confined in the active region for the operation and not being scattered or absorbed by other layers. Therefore, a higher OCF is required. Usually in laser operation the value of OCF is kept 0.4 or more for a stable operation. In SMQW SOA, OCF of 0.3 to 0.6 is acceptable for better performance. In large modulation bandwidth systems, higher OCF is required [15-16]. OCF depends on the molar fraction and thus related to the material composition [2] which leads to the quantum well and material well materials.

SIMULATIONS
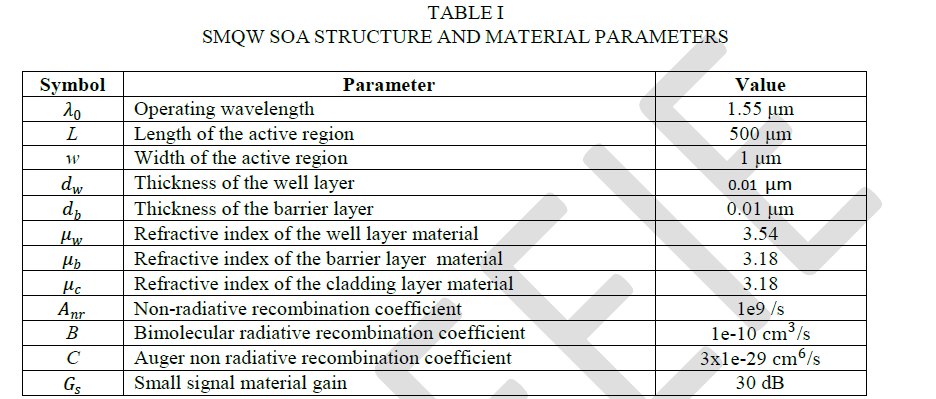
The equations explained in the previous sectionfor SMQW SOA were used to perform various simulations.The computer codes for these equations were generated in MATLAB 7.10.0.The device can be observed using OptiSystem software, if needed. For the simulations presented in this paper, taper length is omitted to avoid complexity of the calculations. The compounds chosen for this study are quite popular for experiments now-a-days. It is 1.55μm InP/InGaAsP system. The most important criteria for selection of well layers and barrier layers arethat the band-gap energy of the well layer (InGaAsP) is lower than the band-gap energy of the barrier layer (InP), and the refractive index is greater for the well material. The lattice parameters are also required to be matched(5.8694 Å in this case) [10].The composition of the compounds expressed in the form of In1−xGaxAsyP1−y [10].Compositions including the molar fraction values are not provided in details here.The values of various parameters in the simulations are provided in Table 1 [14].
image

RESULTS AND DISCUSSION
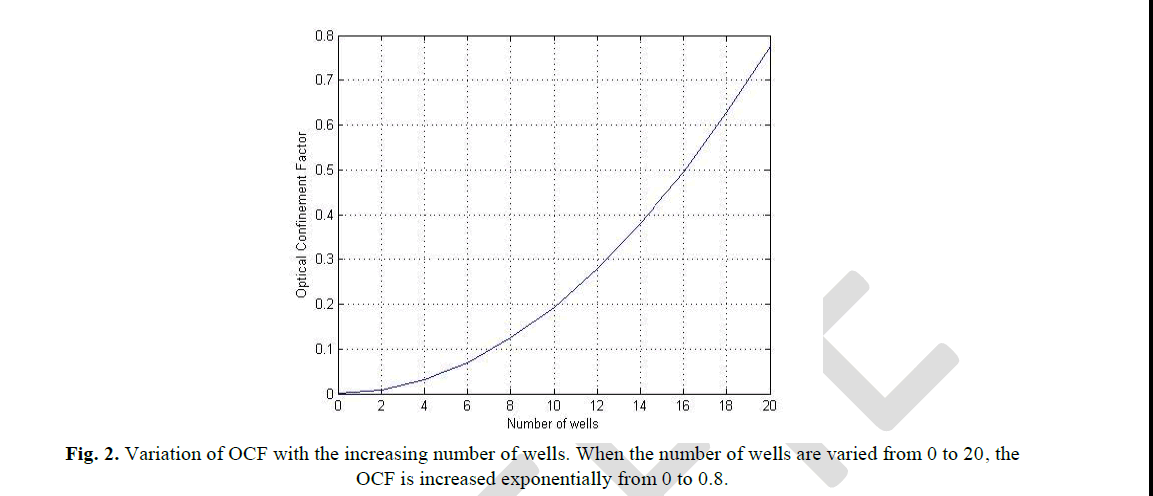
The change in OCF is observed for variation of different structure parameters, e.g., number of quantum wells, number of barriers, well layer thickness and barrier layer thickness.Fig. shows the change in OCF due to the variation of the number of well layers between 0 and 20. The results indicate that with the increase in number of well layers, OCF is increased exponentially with the values between 0 and 0.8. Fig. 2 presents the dependency of OCF on increasing number of wells in the active region. For lower number of wells the OCF has a lower value. When the complexity of the growing layers is avoided, and there are limitations in choosing higher number of wells, the SMQW SOA can be designed with lower number of well layers. However, the tradeoff would be lower OCF.
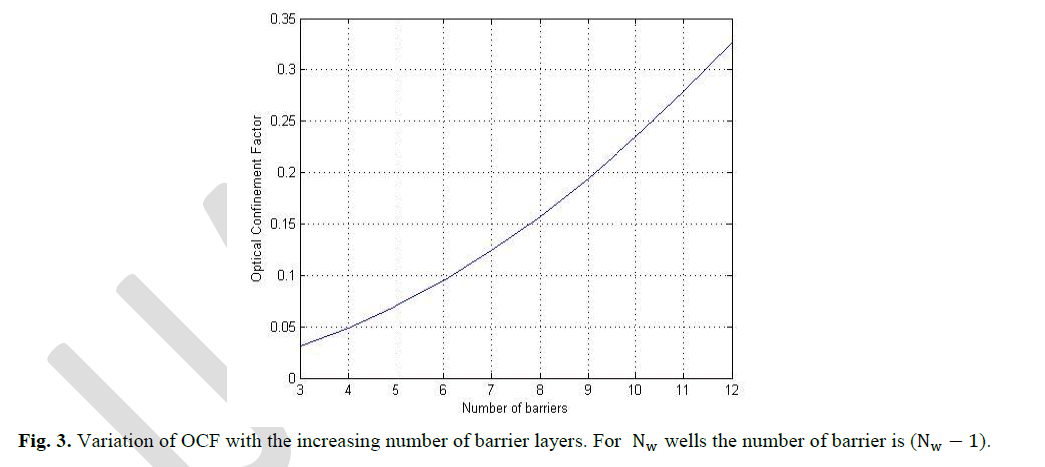
The change of OCF due to the change in the number of barrier layers is shown in Fig. 3. The number of barriers (Nb) is equal to (Nw-1); therefore, the trend of OCF versus number of barriers curve (Fig. 3) is similar to that OCF versus number of wells curve (Fig. 2). When the number of barriers is varied from 3 to 12 (with the number of wells varied from 4 to 13), the OCF changes from 0 to 0.35.
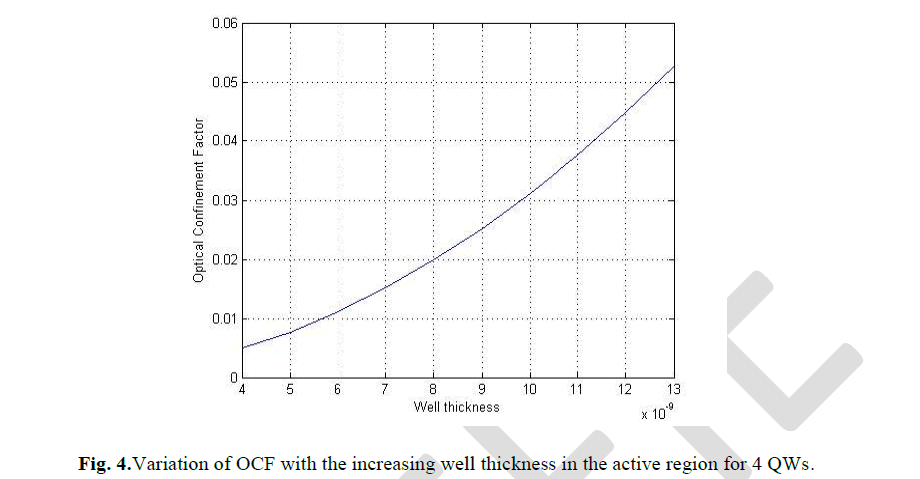
image
image
The change in OCF is obtained through simulations by varying the well layer thickness for 4, 10, 15 number of well layers. Fig.4 shows the OCF versus well thickness curve for 4 welled active region SMQW SOA. When the number of barriers is 3, the OCF varies from approximately 0.005 to 0.06 for the well thickness variation from 4nm to 13nm. The range of OCF here is low.
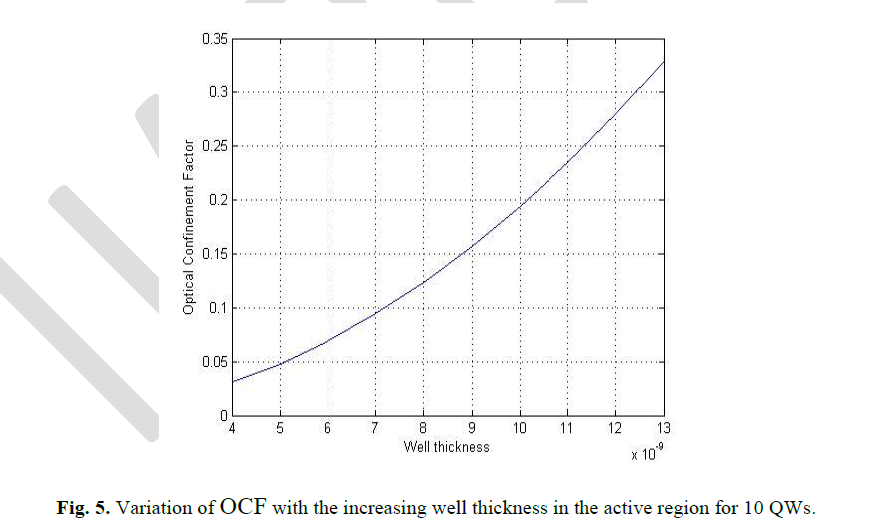
image
For the well thickness range of 4 nm to 13 nm, 10 and 15 well layered devices are also analyzed. Fig. 5 shows the OCF versus well thickness curve for 10 welled active region SMQW SOA. When the number of barriers is 9, the OCF varies from approximately 0.03 to 0.35 for the well thickness variation from 4nm to 13nm. The range of OCF here is higher than the previous case.
image
Fig. 6 shows the OCF versus well thickness curve for 15 welled active region SMQW SOA. When the number of barriers is 14, the OCF varies from approximately 0.085 to 0.8 for the well thickness variation from 4nm to 13nm. The range of OCF here is higher than both 4 and 10 quantum welled active region.
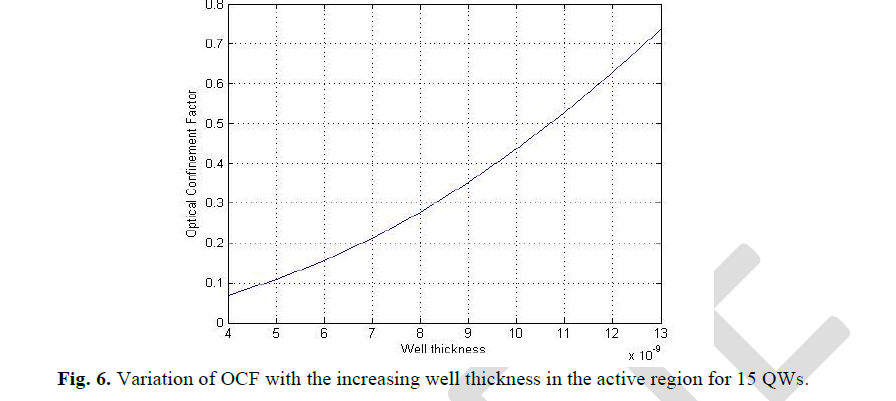image
The results shown in Fig. 4, Fig. 5 and Fig. 6indicate that for the same thickness range (4 nm to 13 nm), SMQW SOA designed with 10 to 15 quantum wells shows higher OCF.
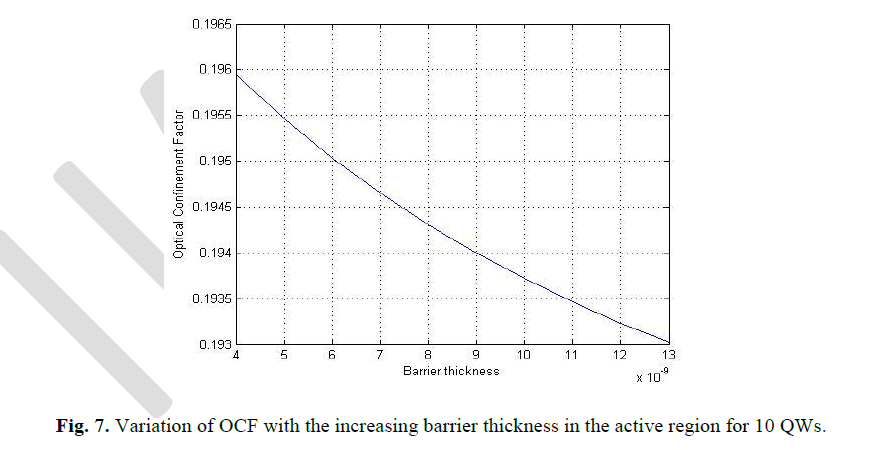
In order to observe the change in OCF for different barrier layer thicknesses, the barrier thickness is varied from 4 nm to 13 nm. The OCF versus barrier thickness graph is determined for both 4 wells and 10 wells. In both of the cases, the OCF shows minor decrement with the increasing barrier thickness. From Fig. 7 it can be established that the OCF does not depend on barrier thickness (for 10 wells). The increase in barrier thickness from 4 nm to 13 nm results in the OCF changes from 0.193 to 0.1965.
image

CONCLUSION
The simulationsand dependency analysis results show that the OCF is highly sensitive to the change in well thickness and number of well layers, and less sensitive to the change in barrier thickness. The target for a device structure is to use the design parameters that lead to better OCF. Analysisof the various graphs indicates that when the number of well layers in a SMQW SOA is varied from 10 to 15 with 10 nm to 13 nm of well layer thickness, it would be possible to obtain a better OCF. High OCF leads to higher stability of the device. It affects the modal condition (TE or TM, single or multiple modes), divergence as well as the threshold current conditions [17]. Therefore, OCF is very important while designing a SMQW SOA. A major drawback of using SOA is the pattern effect; however, solutions are available such as using Lyot filter [18].

References