ISSN ONLINE(2278-8875) PRINT (2320-3765)
ISSN ONLINE(2278-8875) PRINT (2320-3765)
Manipalli VS RajaSekhar1, K.Padma2
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering
A single-objective Particle Swarm Optimization (PSO) approach to tune the parameters of a Thyristor Controlled Series Compensator (TCSC), for minimizing the cost of generation, real power loss and improve the voltage stability L-index. In this paper, TCSC FACTS device is incorporated in solving optimal power flow problems using Particle Swarm Optimization (PSO) for a standard IEEE 30 bus system. Series compensation has been successfully utilized for many years in electric power networks. With Series compensation, it is possible to increase the transfer capability of existing power transmission systems at a lower investment cost and with a shorter installation time compared to the building new, additional lines. This is due to the inherent ability of series capacitors to achieve. Results for optimization of total cost with and without TCSC installation by considering the limits on generator real and reactive power outputs, bus voltages and transformer tapings have been obtained.
Keywords |
| Particle Swarm Optimization (PSO), Optimal Power Flow (OPF), FACTS, TCSC, Power System |
I. INTRODUCTION |
| The increasing industrialization, urbanization of the life style has lead to increasing dependency on the electrical energy. This has resulted into rapid growth has resulted into few uncertainties. Power disruptions and individual power outages are one of the major problems and effect the economy of any country. Recent development of power electronics introduces the use of Flexible AC Transmission System (FACTS) controllers in power systems. FACTS controllers are capable of controlling the network condition in a very fast manner and this unique feature of FACTS can be exploited to improve the stability of power system. TCSC is one of the important members of FACTS family that is increasingly applied by the utilities in modern power system with long transmission lines. Optimal Power Flow (OPF) is an important optimizing tool for modern power system operation and planning which helps to maintain the economy of the power system [1, 2].Particle Swarm Optimization (PSO) is an optimization tool and it is a stochastic, populationbased search and optimization algorithm for problem solving. Particle Swarm Optimization (PSO) technique developed by Dr. Eberhart and Dr. Kennedy in 1995, inspired by social behaviour of bird flocking or fish schooling. The Particle swarm optimization (PSO) is becoming very popular because of its simplicity of implementation. . As compared with other optimization methods, it is faster and more efficient. To obtain performance of TCSC, PSO is included in Optimal Power Flow (OPF) technique. OPF seeks to optimize a certain objective, subject to the network power flow constraints and system and equipment operating limits [3-5]. |
| In present work, Section 2 deals with general problem formulation for Optimization problem. In Section 3, Particle Swarm Optimization algorithm and its application to OPF is discussed in detail. Section 4 deals with Thyristor Control Series Compensator (TCSC) installation in power system and finally in Section 5 the results obtained and comparison graphs for IEEE 30 bus system without and with TCSC are presented. |
II. PROBLEM FORMULATION |
| The standard OPF problem can be formulated as a constrained optimization problem mathematically as follows: Minimize f(x) |
| Subjected to g(x)=0 |
| h(x) ≤ 0 (1) |
| where f(x) is the objective function g(x) represents the equality constraints h(x) represents the inequality constraints and x is the vector of the control variables such as generator real power Pg generator voltages Vg transformer tap setting T. |
| A. Objective Function |
| The most commonly used objective in the OPF problem formulation is the minimization of the total operation cost of the fuel consumed for producing electric power within a schedule time interval (one hour). The individual costs of each generating unit is assumed to be function of only real power generation and are represented by quadratic curves of second order[4]. |
| Where ai,bi and ci are the cost coefficients of generator at bus . The objective of OPF can be changed to maximization of fitness correspondingly as follows: Maximize |
| fitness=1/F |
| B. Types of constraints |
| The above power generation equation can be subjected to two types of constraints. |
| 1) Equality Constraints: |
| The equality constraints are the power flow equations describing bus injected active and reactive powers of the ith bus. |
| The active and reactive power injections at 24th bus are defined in the following equation: |
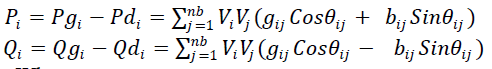 |
| Where |
 |
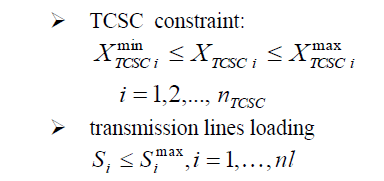 |
III.PARTICLE SWARM OPTIMIZATION IN OPTIMAL POWER FLOW |
| The most commonly used objective in the OPF [5] problem formulation is the minimization of the total operation cost of the fuel consumed. Figure 1 shows the search mechanism of PSO. Each particle moves from the current position to the next one according to the present values. Generally, the fitness function is same the objective functions. The local best of other particles in the population should be changed if the present fitness function value is better than the previous. Repeat the new searching points until the maximum number of generations reached. 150 generations are set in this paper as the stopping criteria. |
| The particles continue flying and seeking solution and hence the algorithm continues until a pre-specified numbers of maximum iterations are exceeded or exit criteria are met. The accuracy and rate of convergence of the algorithm depends on the appropriate choice of particle size, maximum velocity of particles and inertia weight. However, no specific guideline is available to select the particle size. Moreover, it also varies from problem to problem. As a result, one has to choose it by trial and error. The maximum velocity of individual particles should be chosen very judiciously. If the maximum velocity is too high, the particles may fly past the best solution without discovering it and if it is too low particles may fail to explore sufficiently beyond local solutions. |
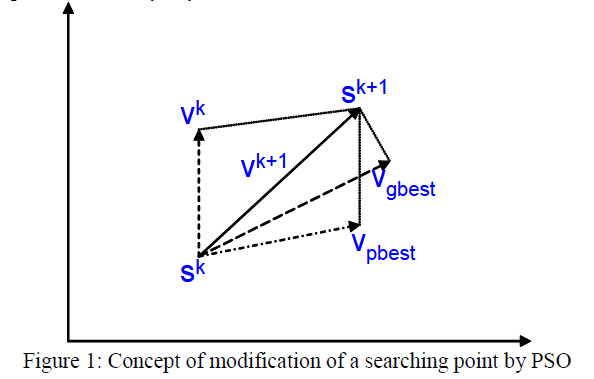 |
| In figure 1, it shows the concept of modification of PSO. Each particle moves from the current position to the next one according to the present values. Generally, the fitness function is same the objective functions. The local best of other particles in the population should be changed if the present fitness function value is better than the previous. |
 |
 |
| 3. For each particle, evaluate the fitness, if all decisions variables are within the search ranges. |
| 4. Compare the particleâÃâ¬ÃŸs fitness evaluation with its previous p-best. If the current value is better than the previous pbest location equal to the current location in the d-dimensional search space. |
| 5. Compare the best current fitness evaluation with the population g-best. If the current value is better than population g-best, then reset the g-best to the current best position and the fitness value to current fitness value. |
| 6. Repeat steps 2-5 until a stopping criterion, such as sufficiently good g-best fitness or a maximum number of iterations is met. |
| B. Algorithm application to OPF: |
| The PSO algorithm applied to OPF can be described in the following steps. |
| Step 1: Input parameters of system, and specify the lower and upper boundaries of each control variable. |
| Step 2: The particles are randomly generated between the maximum and minimum operating limits of the generators. |
| Step 3: Calculate the value of each particle using objective function. |
 |
| Step 7: Modify the position of each particle according to (9). If a particle violates its position limits in any dimension, set its position at proper limits. Calculate each particleâÃâ¬ÃŸs new fitness; if it is better than the previous xgbest the current value is set to be xgbest |
| Step 8: To each particles of the population, employ the Newton-Raphson method to calculate power flow and the transmission loss. |
| Step 9: Update the time counter t=t+1 |
| Step 10: If one of the stopping criteria is satisfied then go to step 11. Otherwise go to step 6. |
| Step 11: The particle that generates the latest pgbest is the global optimum |
| C. Voltage Stability Index (L-index) Computation: |
| The voltage stability L-index [6] is a good voltage stability indicator with its value change between zero (no load) and one (voltage collapse). Moreover, it can be used as a quantitative measure to estimate the voltage stability margin against the operating point. For a given system operating condition, using the load flow (state estimation) results, the voltage stability L-index is computed as given in equation |
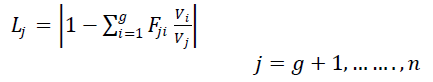 |
IV. POWER FLOW INCLUDING FACTS CONTROLLERS |
| Thyristor Controlled Series Compensation (TCSC) is as shown in figure 2. In There have been significant activities and achievement in the research and application of flexible AC transmission systems (FACTS). Thyristor Controlled Series Compensation (TCSC) is an important device in the FACTS family. It can have various roles in the operation and control of power systems, such as scheduling power flow; decreasing unsymmetrical components; reducing net loss; providing voltage support; limiting short-circuit currents; mitigating sub synchronous resonance (SSR); damping the power oscillation and enhancing-transient stability. TCSC controls the active power transmitted by varying the effective line reactance by connecting a variable reactance in series with line [7]. |
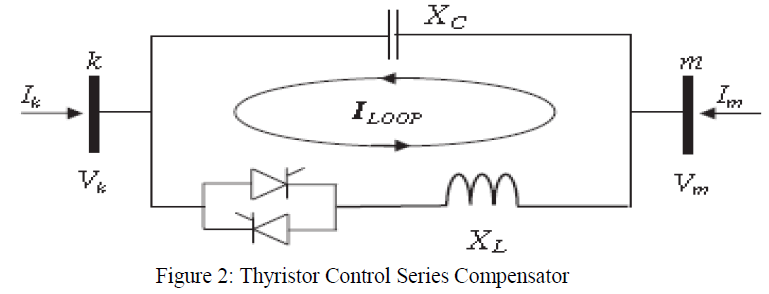 |
| In fig 2, it shows the equivalent circuit of a thyristor controlled series compensation (TCSC). |
| The transfer admittance matrix of the variable series compensator is given by |
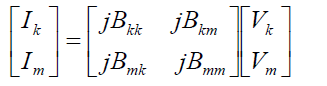 (11) (11) |
| For inductive operation we have |
 |
| V. RESULTS AND DISCUSSION |
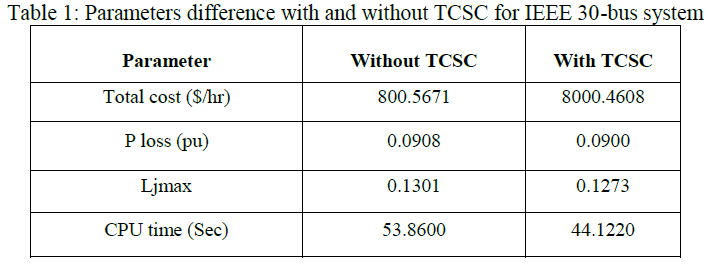
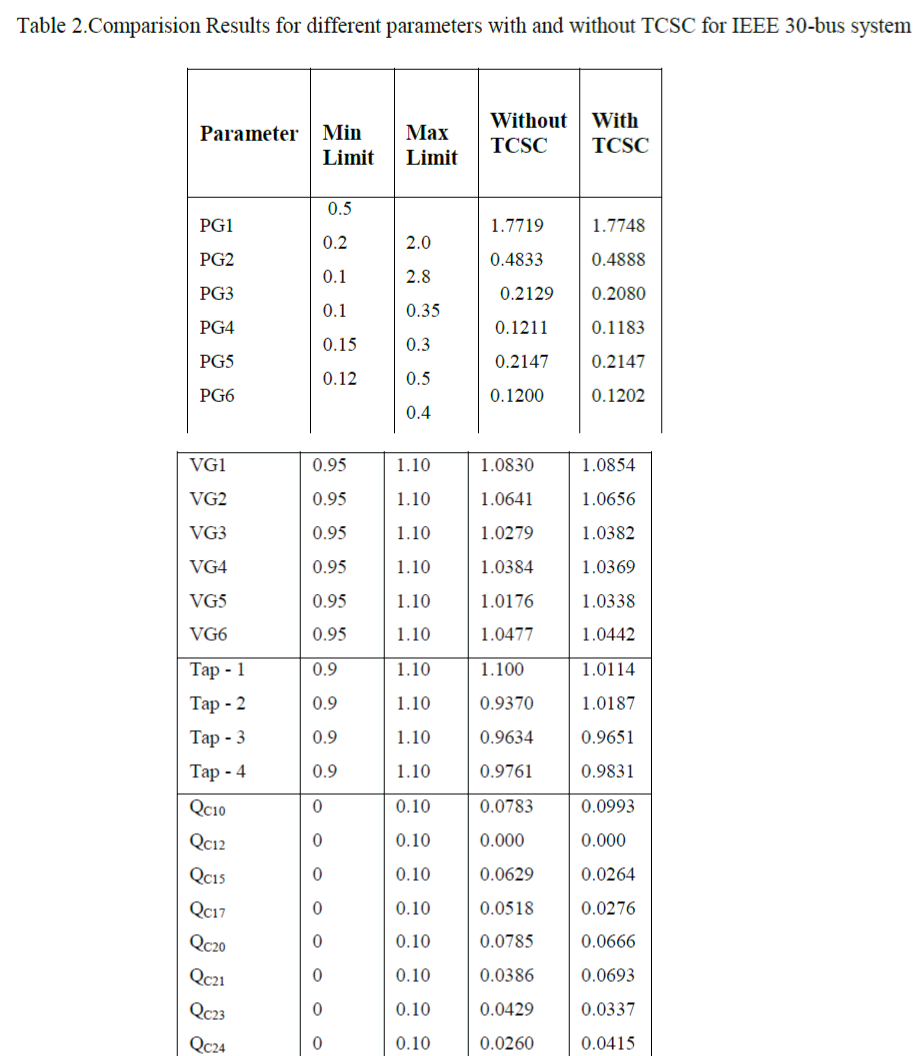
| The research work carried out broadly touches upon the aspects of power system operation and analysis for obtaining reduced operating costs, reduction in power loss and improved voltage stability of the system.The major contributions of the thesis is the investigation on the performance of FACTS device. The Particle Swarm Optimization (PSO) technique has been applied to the OPF problems and has been compared with other OPF techniques reported in the literature. A PSO technique has been developed for TCSC facts device, in which performance with TCSC device exhibits best results compared to without TCSC device. |
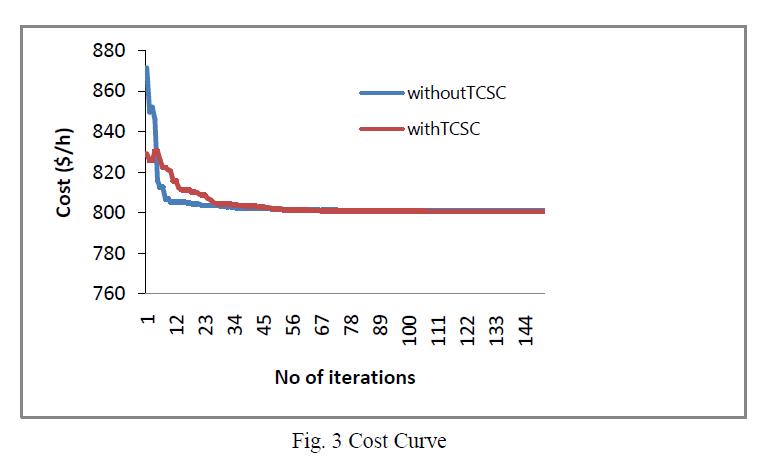 |
| In the fig 3, it shows the graph of cost vs. no .of iterations. In Y-axis cost is in $/h. From the above graph it is clear that the cost becomes low on using TCSC (red line) when compared to the cost without TCSC. |
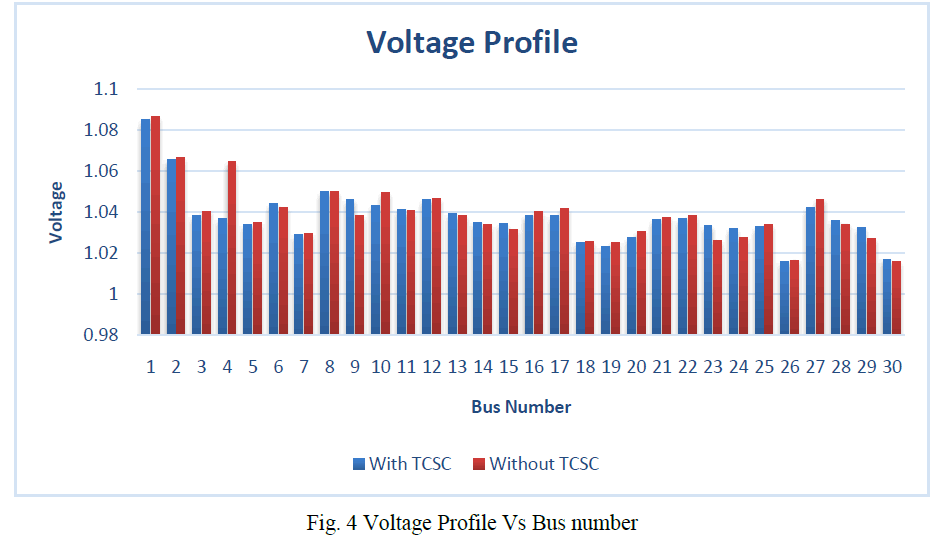 |
| In the fig 4, it shows the graph of voltage Vs bus no. Inserting TCSC (red line) at 27th bus, voltage profile increases when compared to the voltage profile without TCSC (blue line). |
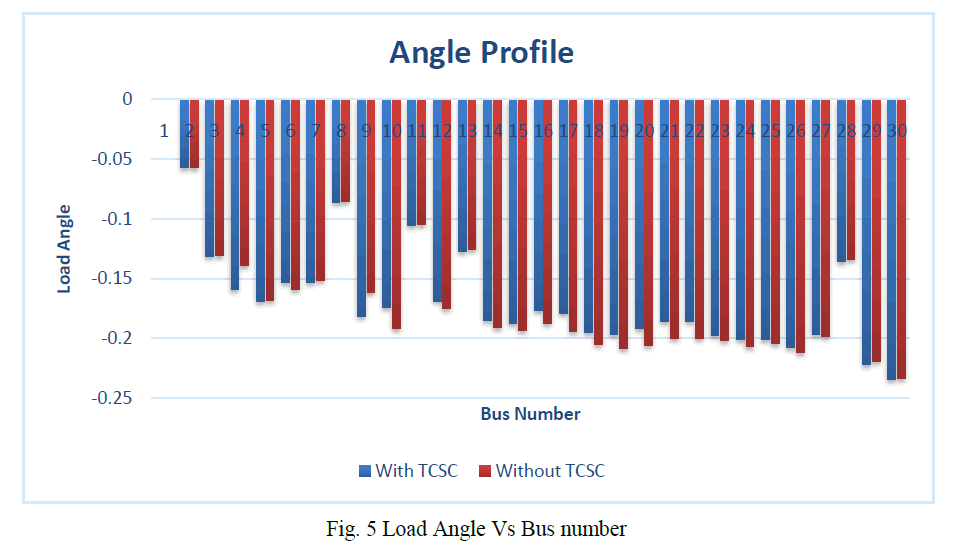 |
| In the fig 5, it shows the graph of load angle Vs bus no. Inserting TCSC (red line) at 27th bus, load angle was improved when compared to the load angle without TCSC (blue line). |
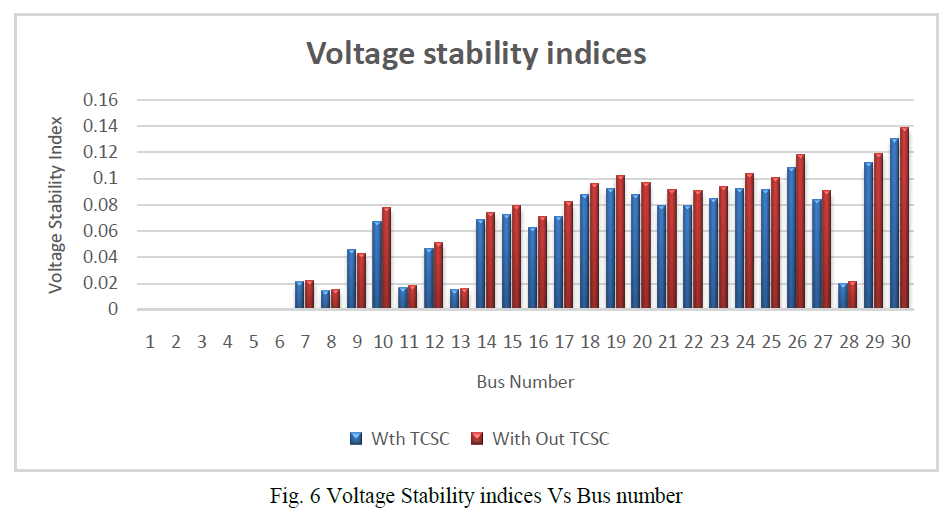 |
| In the fig 6, it shows the graph of voltage stability index Vs bus no. Inserting TCSC (red line) at 27th bus, voltage stability index was improved when compared to voltage stability index without TCSC (blue line). |
 |
 |
VI. CONCLUSION |
| TCSC was installed in the IEEE 30 bus system and the stabilized voltages and reduction MVA loading of the transmission lines has been observed. PSO technique was employed as it possesses advantages of modelling flexibility, sure and fast convergence, less computational time over other heuristic methods. In this research work, Particle Swarm Optimization (PSO) technique was used effectively to solve the OPF problem. The performance of the system has been analyzed by comparing the cost of generation, real power loss, improvement of voltage profiles, voltage angles and improvement of voltage stability L-index. |
References |
|