International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Menu

ISSN ONLINE(2278-8875) PRINT (2320-3765)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

PERFORMANCE analysis of WAVELETS in IMAGE DE-NOISING

S. Naresh1, A. S. Srinivasa Rao2
  1. PG student (VLSI SD), Dept of ECE, AITAM, Tekkali, Srikakulam, Andrapradesh, India
  2. Professor, Dept. of ECE, AITAM, Tekkali, Srikakulam, Andrapradesh, India
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Abstract

Wavelet transforms have become one of the most important and powerful tool of signal representation. Nowadays, it has been used in image processing, data compression, and signal processing. Here, we are discussing about the basic concept for Wavelet Transforms and the fast algorithm of Wavelet Transform. Now-a-days the wavelet theorems make up very popular methods of image processing, de-noising and compression. Considering that the Haar functions are the simplest wavelets, these forms are used in many methods of discrete image transforms and processing. The image transform theory is a well known area characterized by a precise mathematical background, but in many cases some transforms have particular properties which are not still investigated. This paper for the first time presents graphic dependences between the types of wavelet approaches for de-noising. Some properties of the Haar, Daubechies 1 and 2, coif-let 1 and 5, Symlet-8 and reverse bi-orthogonal wavelets spectrum were investigated. Here, i am using different types of wavelet approaches for finding the Mean Square Error (MSE) and Peak Signal-to-Noise Ratio (PSNR) based approach for de-noising the image. For removing the noise from the image wavelet techniques gives good improvement in recovering the original image. Result will shows the recovery of original images along with noisy images.

Keywords
Daubechies and coif-let Transforms Mean Square Error and Symlet wavelet.

I. INTRODUCTION
An image is affected by noise in its acquisition and processing. The de-noising techniques are used to remove the additive noise while retaining as much as possible the important image features. In the recent years there has been an important amount of research on wavelet thresholding and threshold selection for images de-noising [1], because wavelet provides an appropriate basis for separating noisy signal from the image signal. The motivation is that as the wavelet transform is good at energy compaction, the small coefficients are more likely due to noise and large coefficient due to important signal features [1]-[3]. These small coefficients can be threshold without affecting the significant features of the image. In fact, the thresholding technique is the last approach based on wavelet theory to provide an enhanced approach for eliminating such noise source [4], [5] and ensure better image quality [6], [7]. Thresholding is a simple non-linear technique, which operates on one wavelet coefficient at a time. In its basic form, each coefficient is threshold by comparing against threshold, if the coefficient is smaller than threshold, set to zero; otherwise it is kept or modified. Replacing the small noisy coefficients by zero and inverse wavelet transform on the result may lead to reconstruction with the essential signal characteristics and with less noise. Since the work of Donohue & Johnston [3], there has been much research on finding thresholds, however few are specifically designed for images [14].
Unfortunately, this technique has the following disadvantages:
1) It depends on the correct election of the type of thresholding, e.g., Oracle Shrink, Visu Shrink (soft-thresholding, hardthresholding, and semi-soft-thresholding), Sure Shrink, Bayesian soft thresholding, Bayesian MMSE estimation, Thresholding Neural Network (TNN), due to Zhang, Normal Shrink, , etc. [1]-[5], [8].
2) It depends on the correct estimation of the threshold which is arguably the most important design parameter,
3) It doesn't have a fine adjustment of the threshold after their calculation,
4) It should be applied at each level of decomposition, needing several levels, and
5) The specific distributions of the signal and noise may not be well matched at different scales.
Therefore, a new method without these constraints will represent an upgrade. On the other hand, similar considerations should be kept in mind regarding the problem of image compression based on wavelet thresholding.

II. BIDIMENSIONAL DISCRETE WAVELET TRANSFORM
The Bi-dimensional Discrete Wavelet Transform (DWT-2D) [6], [7], [12] corresponds to multi-resolution approximation expressions. In practice, multi-resolution analysis is carried out using 4 channel filter banks (for each level of decomposition) composed of a low-pass and a high-pass filter and each filter bank is then sampled at a half rate (1/2 down sampling) of the previous frequency. By repeating this procedure, it is possible to obtain wavelet transform of any order. The down sampling procedure keeps the scaling parameter constant De-noising and Compression in Wavelet Domain via Projection onto Approximation Coefficients (equal to ½) throughout successive wavelet transforms so that is benefits for simple computer implementation. In the case of an image, the filtering is implemented in a separable way be filtering the lines and columns. Note that [6], [7] the DWT of an image consists of four frequency channels for each level of decomposition. For example, for i-level of decomposition we have:
LLn, i: Noisy Coefficients of Approximation.
LHn, i: Noisy Coefficients of Vertical Detail,
HLn, i: Noisy Coefficients of Horizontal Detail, and
HH n, i: Noisy Coefficients of Diagonal Detail.
The LL part at each scale is decomposed recursively, as illustrated in Fig. 1 [6], [7].
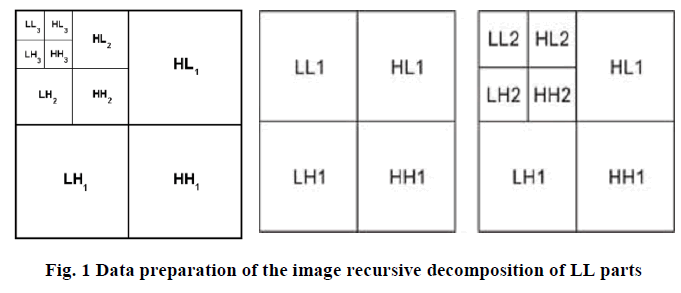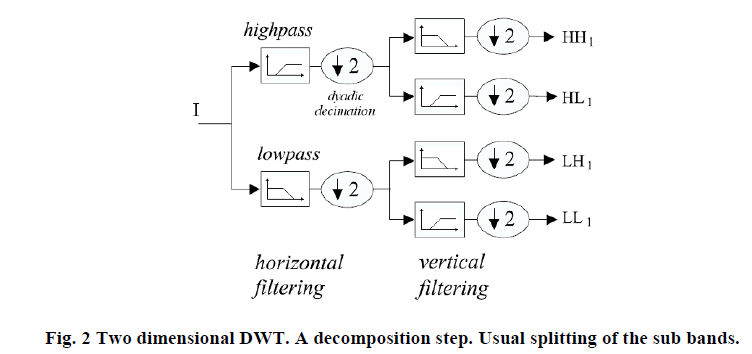
image
To achieve space-scale adaptive noise reduction, we need to prepare the 1-D coefficient data stream which contains the space-scale information of 2-D images. This is somewhat similar to the “zigzag” arrangement of the DCT (Discrete Cosine Transform) coefficients in image coding applications. In this data preparation step, the DWT-2D coefficients are rearranged as a 1-D coefficient series in spatial order so that the adjacent samples represent the same local areas in the original image. Figure 2 shows the interior of the DWT-2D with the four sub bands of the transformed image [51], which will be used in Fig.3. Each output of Fig. 2 represents a sub band of splitting process of the 2-D coefficient matrix corresponding to Fig. 1.
A. Wavelet Noise Thresholding:
The wavelet coefficients calculated by a wavelet transform represent change in the image at a particular resolution. By looking at the image in various resolutions it should be possible to filter out noise, at least in theory. However, the definition of noise is a difficult one.
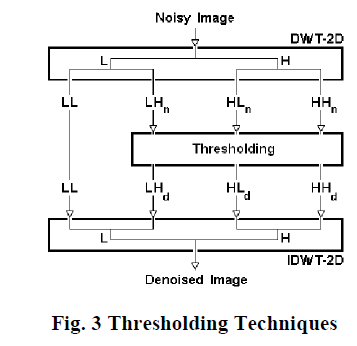
image
In fact, "one person's noise is another's signal". In part this depends on the resolution one is looking at. One algorithm to remove Gaussian white noise is summarized by D. L. Donohue and I. M. Johnston [2], [3], and synthesized in Fig. 3.
image
The algorithm is:
1) Calculate a wavelet transform and order the coefficients by increasing frequency. This will result in an array containing the image average plus a set of coefficients of length 1, 2, 4, 8, etc. The noise threshold will be calculated on the highest frequency coefficient spectrum (this is the largest spectrum).
2) Calculate the median absolute deviation(mad) on the largest coefficient spectrum. The median is calculated from the absolute value of the coefficients. The equation for the median absolute deviation is shown below:
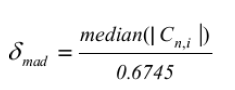image
where Cn,i may be LHn,i , HLn,i , or HHn,i for i-level of decomposition. The factor 0.6745 in the denominator rescales the numerator so that mad „δmad‟ is also a suitable estimator for the standard deviation for Gaussian white noise [5].
3) For calculating the noise threshold „λ‟ we have used a modified version of the equation that has been discussed in papers by D.L. Donohue and I.M. Johnston. The equation is:
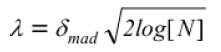image
Where N is the number of pixels in the sub-image, i.e., HL, LH or HH.
For all higher bands (LH, HL and HH) the de-noising can be achieved by applying a thresholding operator to the wavelet coefficients in the transform domain followed by reconstruction of the signal to the original image in spatial domain. In our proposed method, soft shrinkage and Median Absolute Difference (MAD) are used. The scaled MAD noise estimator is calculated by (4).
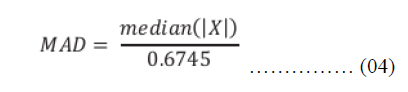image
where X is the high frequency sub-bands coefficients. From the estimated noise, the non linear threshold T is calculated by (5)
image
The noise free sub-bands are obtained by using adaptive thresholding. Finally, the noise free image is obtained by taking the inverse SWT using the modified high frequencies sub-bands and the low frequency sub band of SWT.
4) Apply a thresholding algorithm to the coefficients.

3. Estimation of Parameters for Normal Shrink:
This section describes the method for computing the various parameters used to calculate the threshold value (TN), which is adaptive to different sub band characteristics.
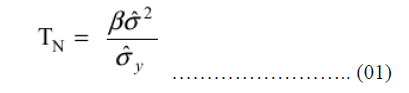image
Where, the scale parameter „β‟ is computed once for each scale using the following equation:
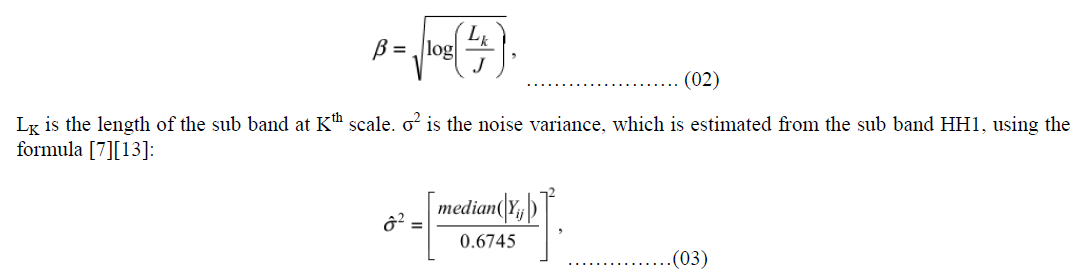image
Yij median ∈ Yij sub band HH1 and „σy‟ is the standard deviation of the sub band under consideration computed by using the standard MATLAB command. To summarize, the proposed method is named as Normal Shrink which performs soft thresholding with the data driven sub band dependent threshold TN.
Image De-noising Algorithm:
This section describes the image de-noising algorithm, which achieves near optimal soft thresholding in the wavelet domain for recovering original signal from the noisy one. The algorithm is very simple to implement and computationally more efficient. It has following steps:
1. Perform multi-scale decomposition [11] of the image corrupted by Gaussian noise using wavelet transform.
2. Estimate the noise variance σ2 using equation (3).
3. For each level, compute the scale parameter β using equation (2).
4. For each sub band (except the low pass residual)
a) Compute the standard deviation σy. b) Compute threshold TN using equation (1).
c) Apply soft thresholding to the noisy coefficients.
5. Invert the multi-scale decomposition to reconstruct the denoised image fˆ.
EXPERIMENTAL RESULTS:
The proposed algorithm tested for 256x256 images. It is tested for various levels of noise values and also compared with different type of wavelet techniques. Figure 2 shows the de-noising performance of the proposed algorithm. Proposed method and based soft shrinkage and different Wavelet Technique approaches with different noise variance.
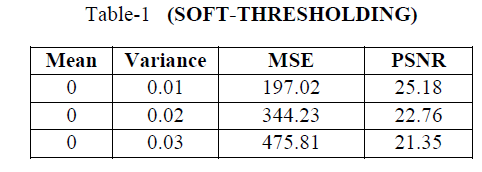
SOFT THRESHOLDING RESULTING IMAGES:
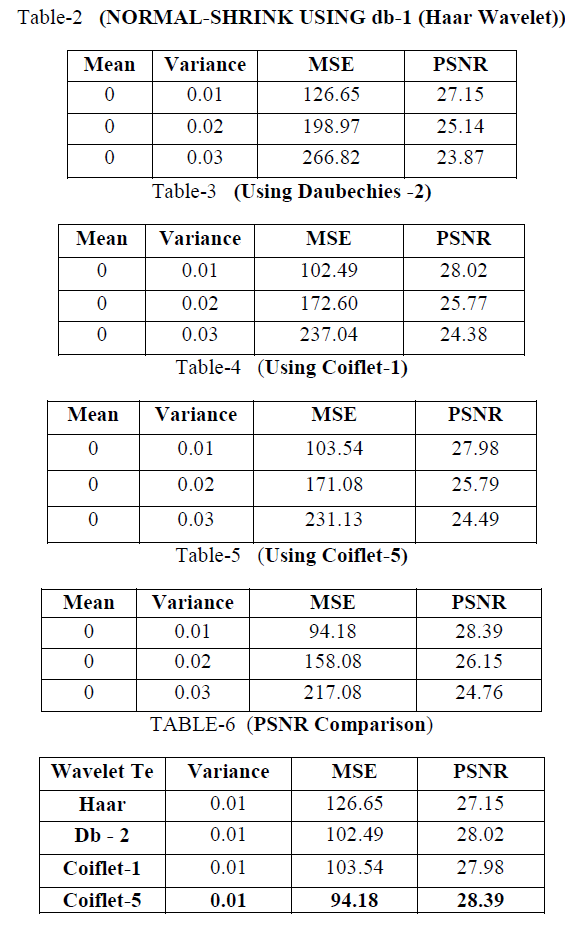
image
image
Below tabular forms shows that the Mean Square Error (MSE) and Peak Signal to Noise Ratio (PSNR) of each approach of different types of wavelet techniques.
image
image

CONCLUSION
Here, we are calculating the simple soft thresholding and normal shrink of an image. For de-noising the thresholding value of an image is mandatory. Hence, we used simple soft thresholding technique. Once thresholding value is calculated, then need to find the value of normal shrinkage. For this am using different types of wavelet techniques like Haar wavelet, Daubechies -1 and 2, Coif-let wavelet 1 and 5. Among all these coif-let 5 will gives the best peak signal-tonoise ratio (PSNR). Hence among all these wavelets coif-let 5 is the best approach for de-noising an image. While comparing with remaining wavelets the resultant Mean Square Error (MSE) and peak signal-to-noise ratio (PSNR) are the best for coif-let wavelet only. This will gives the best result for calculating an image de-noising. Likewise if remaining other wavelets supports for de-noising there may be an opportunity for calculating the better Mean Square Error (MSE) and Peak Signal-to-Noise Ratio (PSNR). Which will gives the best MSE and PSNRs that particular wavelet technique will be the best for calculating the best image de-noising.

References